排序分类
插入排序:直接插入排序,希尔排序
选择排序:选择排序,堆排序
交换排序:冒泡排序,快速排序
归并排序
插入排序
直接插入排序
相当于摸牌,例如我们现在手上有{2,4,5,6}这些牌,当下一张是3的时候我们要将3插入到2和4当中,那么对于数组我们就要 把4,5,6 都往后挪,给3让出一个位置,这里演示以下往后挪的过程。
现有2,4,5,6
3先和6比,3应该放在6的前面,也就是3和6交换,交换后2,4,5,3,6
3再和5比,3应该放在5的前面,也就是3和5交换,交换后2,4,3,5,6
3再和4比,3应该放在4的前面,也就是3和4交换,交换后2,3,4,5,6
3再和2比,3应该放在2的后面,3本来就在2的后面,那就不用交换了,这就结束了
很明显,这个要用到循环,既然用到,那么就要有结束条件--------插入的数大于前一个数。
这个是一个,模拟的过程,但我们一般情况下遇到的都是一个固定长度的数组,也就是说,在不动空间的条件下只是比较交换。
假设现在是这样的一个数组{ 2,3,1,4,2,5,2,0}我们可以先从第一2位置开始排,接着就是3,1,4...把他们放到该放的位置
先排2,结果如下
第一趟:2,3,1,4,2,5,2,0
在排3,和他前面的2进行比较,不用交换,结果如下:
第二趟:2,3,1,4,2,5,2,0
在排1,和前面的3进行比较,需要交换结果如下:
2,1,3,4,2,5,2,0
还没有到达循环结束条件(插入的数大于前一个数)所以需要继续和前面的二进行比较,进行交换,结果如下:
1,2,3,4,2,5,2,0,交换后也没有到达循环结束条件,但是1的前面已经没有数了,这样也是结束了1的排序,所以上面的循环结束条件应该在加一个插入的数下标已经为0;因此第三趟排序结果为:
第三趟:1,2,3,4,2,5,2,0
剩下的数依次类推...
#include<iostream>
#include<vector>
using namespace std;
void swap(int& a, int& b)
{
int tmp=a;
a = b;
b = tmp;
}
int main()
{
vector <int>arr = { 2,3,1,4,2,5,2,0};
cout << "排序前:";
for (int i = 0; i < arr.size(); i++)cout << arr[i] << ' ';
for (int i = 1; i < arr.size(); i++)//i是要排的数
{
int t = i;
for (int j = i - 1; j >=0; j--)//
{
if (arr[t] < arr[j])
{
swap(arr[t--], arr[j]);
}
else
break;
}
}
cout << endl<<"排序后:";
for (int i = 0; i < arr.size(); i++)cout << arr[i] << ' ';
return 0;
}时间复杂度分析
时间复杂度最差的时候:也就是 逆序的时候,下面是他们每次交换后的样子

#include<iostream>
#include<vector>
using namespace std;
void swap(int& a, int& b)
{
int tmp=a;
a = b;
b = tmp;
}
int main()
{
vector <int>arr = {8,7,6,5,4,3,2,1,0};
cout << "排序前:";
for (int i = 0; i < arr.size(); i++)cout << arr[i] << ' ';
cout << endl<<endl;
for (int i = 1; i < arr.size(); i++)//i是要排的数
{
int t = i;
for (int j = i - 1; j >=0; j--)//
{
if (arr[t] < arr[j])
{
swap(arr[t--], arr[j]);
for (int i = 0; i < arr.size(); i++)cout << arr[i] << ' ';
cout << endl;
}
else
break;
}
//cout <<"比较:"<<i<<"次"<<endl;
cout << endl;
}
cout << endl<<"排序后:";
for (int i = 0; i < arr.size(); i++)cout << arr[i] << ' ';
return 0;
}每次交换的次数类似一个等差数列,因此时间复杂度就是O()
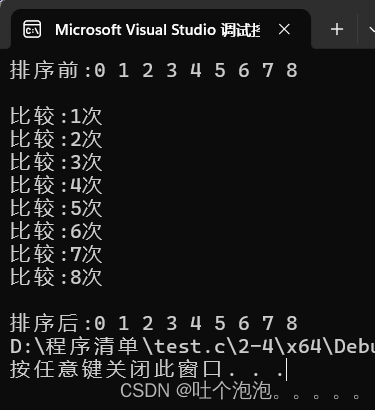
时间复杂度最好的时候也就是正序的时候,每次交换后如下图所示:
#include<iostream>
#include<vector>
using namespace std;
void swap(int& a, int& b)
{
int tmp=a;
a = b;
b = tmp;
}
int main()
{
vector <int>arr = {0,1,2,3,4,5,6,7,8};
cout << "排序前:";
for (int i = 0; i < arr.size(); i++)cout << arr[i] << ' ';
cout << endl<<endl;
for (int i = 1; i < arr.size(); i++)//i是要排的数
{
int t = i;
for (int j = i - 1; j >=0; j--)//
{
if (arr[t] < arr[j])
{
swap(arr[t--], arr[j]);
for (int i = 0; i < arr.size(); i++)cout << arr[i] << ' ';
cout << endl;
}
else
break;
}
cout <<"比较:"<<i<<"次"<<endl;
//cout << endl;
}
cout << endl<<"排序后:";
for (int i = 0; i < arr.size(); i++)cout << arr[i] << ' ';
return 0;
}可以看出就算本身是有序的,也得过一遍才可以,因此时间复杂度是O(n)