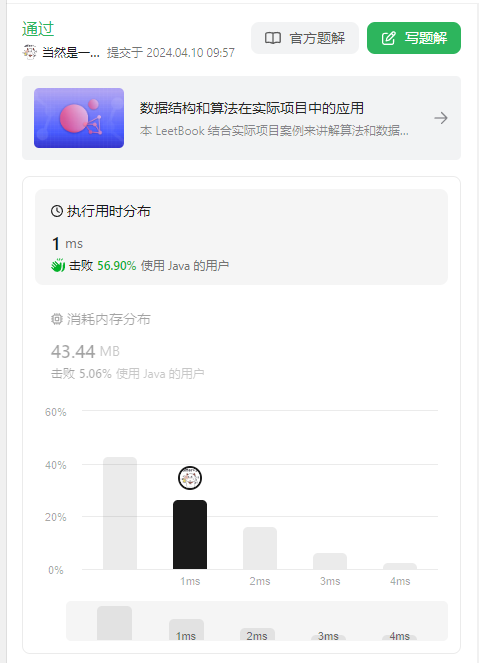
题目:

题解:
char phoneMap[11][5] = {"\0", "\0", "abc\0", "def\0", "ghi\0", "jkl\0", "mno\0", "pqrs\0", "tuv\0", "wxyz\0"};
char* digits_tmp;
int digits_size;
char** combinations;
int combinations_size;
char* combination;
int combination_size;
void backtrack(int index) {
if (index == digits_size) {
char* tmp = malloc(sizeof(char) * (combination_size + 1));
memcpy(tmp, combination, sizeof(char) * (combination_size + 1));
combinations[combinations_size++] = tmp;
} else {
char digit = digits_tmp[index];
char* letters = phoneMap[digit - '0'];
int len = strlen(letters);
for (int i = 0; i < len; i++) {
combination[combination_size++] = letters[i];
combination[combination_size] = 0;
backtrack(index + 1);
combination[--combination_size] = 0;
}
}
}
char** letterCombinations(char* digits, int* returnSize) {
combinations_size = combination_size = 0;
digits_tmp = digits;
digits_size = strlen(digits);
if (digits_size == 0) {
*returnSize = 0;
return combinations;
}
int num = 1;
for (int i = 0; i < digits_size; i++) num *= 4;
combinations = malloc(sizeof(char*) * num);
combination = malloc(sizeof(char*) * digits_size);
backtrack(0);
*returnSize = combinations_size;
return combinations;
}