【C++】用红黑树封装map和set

我们之前学的map和set在stl源码中都是用红黑树封装实现的，当然，我们也可以模拟来实现一下。在实现之前，我们也可以看一下stl源码是如何实现的。我们上篇博客写的红黑树里面只是一个pair对象，这对于set来说显然是不合适的，所以要想让一个红黑树的代码同时支持map和set，就用上模板就可以了

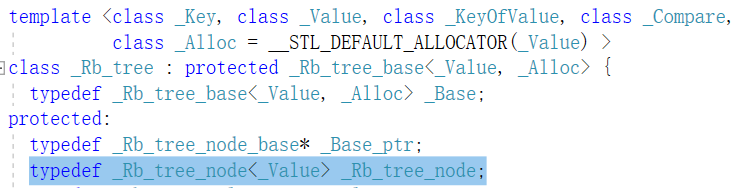
我们来看看stl源码中是如何实现的

前两个模板参数是两个类型，就是我们要在set或map中放入什么

set不是只需要放入一个吗？所以，set在传参数的时候是这么传的

它的前两个传的全是Key，它这么实现还是为了兼容map，map传的是什么呢？我们再来看一下

传的一个是Key，一个是pair类的对象。那pair中不是已经有Key了吗，为什么还要传Key呢？因为一个最简单的原因之一find函数的参数是Key。

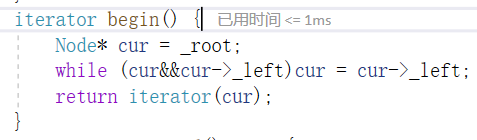
那么看第三个模板参数keyofvalue，传这个类型是为了从value中找到key，因为我们树这个类传给节点类的时候只传了value，如下图：

因为map中value是一个pair对象，set中value就是key，它们的获取方式不一样，所以传这个参数是为了实现仿函数，来取出key值用于比较。

那么了解了这个大体的结构之后，下一个就是要实现我们的迭代器了，我们其实可以在红黑树中实现一个树形的迭代器，然后map和set再封装一层就行了，其实我们的迭代器就是一个类，它用来实现类似于指针的一些操作，所以我们就用指针来当作这个类的成员变量，在这个类的基础上实现迭代器的功能。

在实现迭代器的时候，最关键的一个函数就是重载++，这里迭代器++肯定是按中序，因为这样才有意义，有顺序，那么我们如何通过一个节点找到它的中序遍历的下一个节点呢？这其实是有规律的。比如我们看这样一颗红黑树

首先我们中序遍历是左子树 根 右子树

1.假设这个节点有右子树，那么这个节点之后就是它的右子树的中序的第一个节点，就是右子树中最左边的节点

2.假设这个节点没有右子树，那么走完这个节点以后以这个节点为根的树就走完了，假如它是它父亲的左孩子，那么就该走它的父亲，如果它是它父亲的右孩子，那么它父亲也走完了，就按照此规律走它的爷爷。

有了这个理论基础，我们就可以来实现了。

同样--的话跟++是完全相反的，反过来的遍历顺序就是右子树，根，左子树，然后我们再分别去看这棵树有没有左子树，如果有，那就走左子树中第一个该走的节点，就是左子树中最右节点；如果没有，那就看它是它父亲的什么节点，一直往上找，直到找到它是它父亲的右子树的节点，它父亲就是下一个要遍历的节点。

下面还有一些细节问题，比如说把迭代器写成模板

那么只需要传不同的类型就可以实现const或非const的迭代器

我们const对象要用const版本的迭代器，因为const对象用普通版本的属于权限放大，所以我们要设计const版本的迭代器

我们也要对红黑树的插入函数进行修改，原来插入函数返回一个bool值，但是库中应该是返回一个pair对象，其中first是个迭代器，second是个bool值表示是否新插入

看到这样的代码的时候，这个typename表示后面是一个类型名，因为static静态成员也可以指明类域然后去访问

另外，我们这里为什么传const K呢？因为就算是普通的迭代器我们也不希望key值改变，因为map的key值改了就不满足二叉搜索树了

这是如何使用const_iterator，首先s就是一个普通的map对象，就调用普通版本的begin()

调完之后它返回一个iterator，而我们用的const_iterator去接收的，所以要写个构造函数，用普通迭代器构造出const迭代器

那么下面我们再整体的来展示一下红黑树和map set之间的封装关系

这就是如何用红黑树封装出map和set，下面是所有的代码

RBTree.h

#include<iostream>
#include<assert.h>
using namespace std;

enum col {
	RED,
	BLACK
};
template<class T>
struct RBTreeNode {
	RBTreeNode(const T& data)
		:_left(nullptr)
		,_right(nullptr)
		,_parent(nullptr)
		,_data(data)
		,_col(RED){}

	RBTreeNode* _left = nullptr;
	RBTreeNode* _right = nullptr;
	RBTreeNode* _parent = nullptr;
	T _data;
	col _col=RED;
};
template<class T,class Ptr,class Ref>
struct RBTreeIterator {
	typedef RBTreeNode<T> Node;
	typedef RBTreeIterator<T,Ptr,Ref> self;

	typedef RBTreeIterator<T,  T*,  T&> iterator;
	typedef RBTreeIterator<T, const T*, const T&> const_iterator;

	Node* _node;

	RBTreeIterator(const iterator& it)
		:_node(it._node) {}

	RBTreeIterator(Node*node)
		:_node(node){}

	Ref operator*() {
		return _node->_data;
	}
	Ptr operator->() {
		return &_node->_data;
	}
	bool operator==(const self&s) {
		return _node == s._node;
	}
	bool operator!=(const self& s) {
		return _node != s._node;
	}
	self& operator++() {
		if (_node == nullptr) {
			cout << "end()不能++" << endl;
			assert(false);
		}
		if (_node->_right) {//有右子树，那么这个节点之后就是它的右子树的中序的第一个节点，就是右子树中最左边的节点
			_node = _node->_right;
			while (_node->_left != nullptr)_node = _node->_left;
			return *this;
		}
		else {//没有右子树，直到找到孩子是父亲左子树的那个父亲节点
			Node* parent = _node->_parent;
			while (parent && _node != parent->_left) {
				parent = parent->_parent;
				_node = _node->_parent;
			}
			_node = parent;
			return *this;
		}
			
	}
	self& operator--() {
		if (_node->_left) {
			_node = _node->_left;
			while (_node->_right != nullptr)_node = _node->_right;
			return *this;
		}
		else {
			Node* parent = _node->_parent;
			while (parent && _node != parent->_right) {
				parent = parent->_parent;
				_node = _node->_parent;
			}
			_node = parent;
			return *this;
		}

	}
};

template<class K,class V,class Keyofvalue>
class RBTree {
	typedef RBTreeNode<V> Node;
public:
	typedef RBTreeIterator<V,V*,V&> iterator;
	typedef RBTreeIterator<V,const V*,const V&> const_iterator;

	const_iterator begin()const {
		Node* cur = _root;
		while (cur && cur->_left)cur = cur->_left;
		return const_iterator(cur);
	}
	iterator begin() {
		Node* cur = _root;
		while (cur&&cur->_left)cur = cur->_left;
		return iterator(cur);
	}
	const_iterator end()const {
		return const_iterator(nullptr);
	}
	iterator end() {
		return iterator(nullptr);
	}
	iterator Find(const K& key) {
		Keyofvalue kov;
		Node* cur = _root;
		while (cur) {
			if (kov(cur->_data) < key) {
				cur = cur->_right;
			}
			else if (kov(cur->_data) > key) {
				cur = cur->_left;
			}
			else {
				return iterator(cur);
			}
		}
		return end();
	}
	pair<iterator,bool> insert(const V& data) {
		if (_root == nullptr) {
			_root = new Node(data);
			_root->_col = BLACK;
			return make_pair(iterator(_root),true);
		}
		Node* cur = _root;
		Node* parent = nullptr;
		Keyofvalue kov;
		while (cur) {
			if (kov(cur->_data) < kov(data)) {
				parent = cur;
				cur = cur->_right;
			}
			else if (kov(cur->_data) > kov(data)) {
				parent = cur;
				cur = cur->_left;
			}
			else return make_pair(iterator(cur),false);
		}
			cur = new Node(data);
			Node* ret = cur;
			if (kov(parent->_data) < kov(cur->_data)) {
				parent->_right = cur;
				cur->_parent = parent;
			}
			else {
				parent->_left = cur;
				cur->_parent = parent;
			}
			Node* c = cur;
			Node* p = cur->_parent;
			Node* g = p->_parent;
			Node* u = nullptr;
			while (p && p->_col == RED) {
				if (p == g->_left)u = g->_right;
				else u = g->_left;
				if (u == nullptr || u->_col == BLACK) {
					if (p == g->_left && c == p->_left) {
						RotateR(g);
						p->_col = BLACK;
						g->_col = RED;
					}
					else if (p == g->_right && c == p->_right) {
						RotateL(g);
						p->_col = BLACK;
						g->_col = RED;
					}
					else if (p == g->_left && c == p->_right) {
						RotateL(p);
						RotateR(g);
						c->_col = BLACK;
						g->_col = RED;
					}
					else if (p == g->_right && c == p->_left) {
						RotateR(p);
						RotateL(g);
						c->_col = BLACK;
						g->_col = RED;
					}
					else assert(false);
					break;
				}
				else if (u->_col == RED) {
					p->_col = BLACK;
					u->_col = BLACK;
					g->_col = RED;
					if (g == _root) {
						g->_col = BLACK;
						break;
					}
					else {
						c = g;
						p = c->_parent;
						g = p->_parent;
					}
				}
				else assert(false);
				
			}
			return make_pair(iterator(ret),true);
	}

	void RotateL(Node* parent) {
		Node* subR = parent->_right;
		Node* subRL = subR->_left;
		Node* ppnode = parent->_parent;
		if (subRL)subRL->_parent = parent;
		parent->_right = subRL;
		subR->_left = parent;
		parent->_parent = subR;
		if (parent == _root) {
			_root = subR;
			subR->_parent = nullptr;
		}
		else {
			subR->_parent = ppnode;
			if (ppnode->_left == parent)ppnode->_left = subR;
			else ppnode->_right = subR;
		}

	}


	void RotateR(Node* parent) {
		Node* subL = parent->_left;
		Node* subLR = subL->_right;
		Node* ppnode = parent->_parent;
		if (subLR)subLR->_parent = parent;
		parent->_left = subLR;
		subL->_right = parent;
		parent->_parent = subL;
		if (parent == _root) {
			_root = subL;
			subL->_parent = nullptr;
		}
		else {
			subL->_parent = ppnode;
			if (ppnode->_left == parent)ppnode->_left = subL;
			else ppnode->_right = subL;
		}
	}
	Node* getroot() {
		return _root;
	}


private:
	Node* _root = nullptr;
};

MySet.h


namespace jxh {
	template<class T>
	class set {
		typedef RBTreeNode<T> Node;
		struct keyofvalue {
			const T& operator()(const T&key) {
				return key;
			}
		};
		void _inorder(Node* root) {
			if (root == nullptr)return;
			_inorder(root->_left);
			cout << root->_data << endl;
			_inorder(root->_right);
		}
	public:
		typedef typename RBTree<T, const T, keyofvalue>::iterator iterator;
		typedef typename RBTree<T, const T, keyofvalue>::const_iterator const_iterator;
		iterator begin()
		{
			return _t.begin();
		}

		iterator end()
		{
			return _t.end();
		}
		const_iterator begin()const
		{
			return _t.begin();
		}

		const_iterator end()const
		{
			return _t.end();
		}

		pair<iterator, bool> insert(const T& key)
		{
			return _t.insert(key);
		}

		iterator find(const T& key)
		{
			return _t.find(key);
		}

		void inorder() {
			_inorder(_t.getroot());
		}
	private:
		RBTree<T,const T,keyofvalue> _t;
	};

MyMap.h

namespace jxh {
	template<class K,class V>
	class map {
		typedef RBTreeNode<pair<K,V>> Node;
		struct keyofvalue {
			const K& operator()(const pair<K,V>& kv) {
				return kv.first;
			}
		};
		void _inorder(Node* root) {
			if (root == nullptr)return;
			_inorder(root->_left);
			cout << root->_data.first<<" "<<root->_data.second << endl;
			_inorder(root->_right);
		}
	public:

		//typedef RBTreeIterator<pair<K,V>> iterator;
		typedef typename RBTree<K, pair<const K, V>, keyofvalue>::iterator iterator;
		typedef typename RBTree<K, pair<const K, V>, keyofvalue>::const_iterator const_iterator;

		const_iterator begin()const {
			return _t.begin();
		}
		const_iterator end() const{
			return _t.end();
		}
		iterator begin() {
			return _t.begin();
		}
		iterator end() {
			return _t.end();
		}

		pair<iterator, bool> insert(const pair<K, V>& kv)
		{
			return _t.insert(kv);
		}

		iterator find(const K& key)
		{
			return _t.find(key);
		}

		V& operator[](const K& key)
		{
			pair<iterator, bool> ret = insert(make_pair(key, V()));
			return ret.first->second;
		}

		void inorder() {
			_inorder(_t.getroot());
		}
	private:
		RBTree<K, pair<const K,V>, keyofvalue> _t;
	};