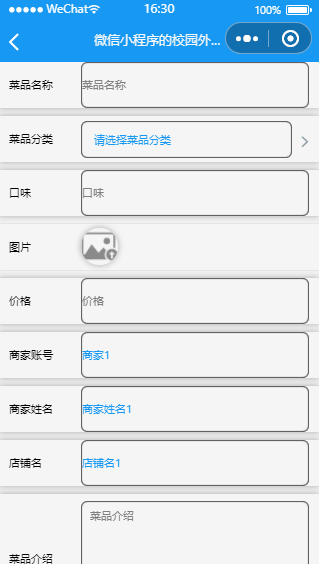
包装器,体现了C++11中的封装性,包装器可以应用于:函数指针,仿函数,lambda
而包装器function的出现刚好也弥补了上述三种语法的不足之处
函数指针写起来较为复杂,而仿函数之间类型不同,lambda则在语法层压根没有类型
而function的目的就是封装它们统一类型。
一、function包装器
//ret = func(x);
// 上面func可能是什么呢?那么func可能是函数名?函数指针?函数对象(仿函数对象)?也有可能
//是lamber表达式对象?所以这些都是可调用的类型!如此丰富的类型,可能会导致模板的效率低下!
template<class F, class T>
T useF(F f, T x)
{
static int count = 0;
cout << "count:" << ++count << endl;
cout << "count:" << &count << endl;
return f(x);
}
double f(double i)
{
return i / 2;
}
struct Functor
{
double operator()(double d)
{
return d / 3;
}
};
int main()
{
// 函数名
cout << useF(f, 11.11) << endl;
// 函数对象
cout << useF(Functor(), 11.11) << endl;
// lamber表达式
cout << useF([](double d)->double { return d / 4; }, 11.11) << endl;
return 0;
}这里的useF在编译时因为参数类型的不同会被实例化出三份,当多次调用传不同参数时就会被实例化出多份,而function包装器就可以很好的解决这个问题。天空一声巨响,可变模板参数包闪亮登场:
std::function在头文件<functional>
// 类模板原型如下
template <class T> function; // undefined
template <class Ret, class... Args>
class function<Ret(Args...)>;
模板参数说明:
Ret: 被调用函数的返回类型
Args…:被调用函数的形参基于function我们就可以对上面的代码进行改造:
template<class F, class T>
T useF(F f, T x)
{
static int count = 0;
cout << "count:" << ++count << endl;
cout << "count:" << &count << endl;
return f(x);
}
double f(double i)
{
return i / 2;
}
struct Functor
{
double operator()(double d)
{
return d / 3;
}
};
int main()
{
// 函数指针
function<double(double)> fc1=f;
cout << useF(fc1, 11.11) << endl;
// 函数对象
function<double(double)> fc2 = Functor();
cout << useF(fc2, 11.11) << endl;
// lambda表达式
function<double(double)> fc3 = [](double d)->double { return d / 4; };
cout << useF(fc3, 11.11) << endl;
return 0;
}
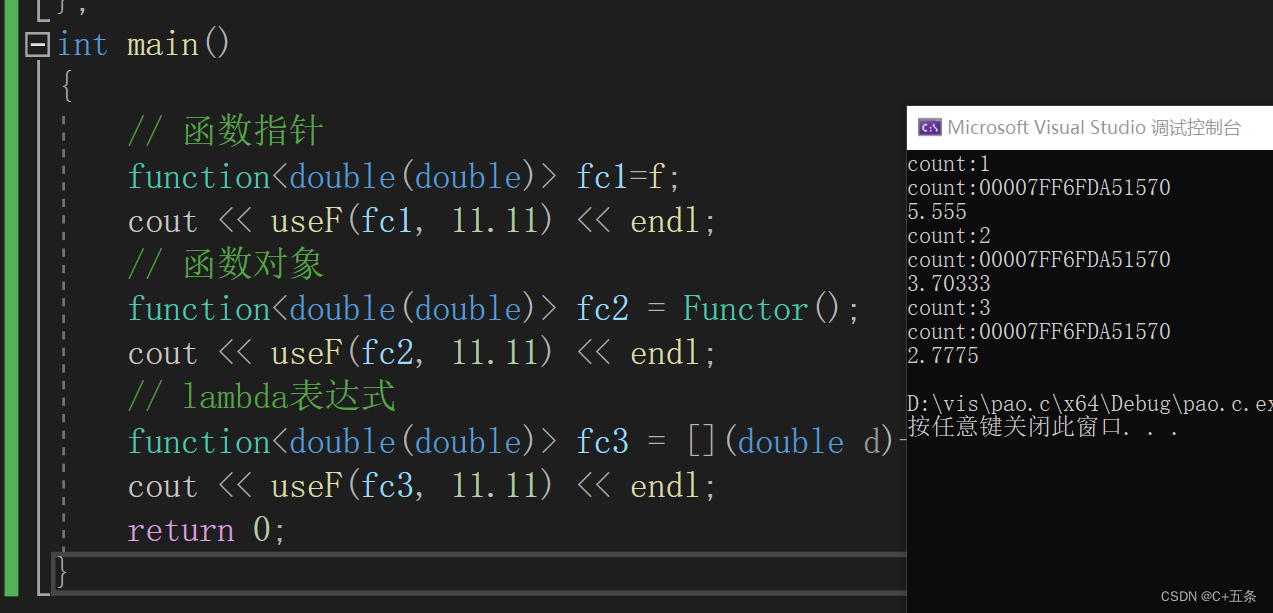
这时三个参数都是function<double(double)>类型的,而这时useF只需要实例化出一份就可以了。
二、function实际应用
根据 逆波兰表示法,求该后缀表达式的计算结果。
有效的算符包括 +、-、*、/ 。每个运算对象可以是整数,也可以是另一个逆波兰表达式。
说明:
- 整数除法只保留整数部分。
- 给定逆波兰表达式总是有效的。换句话说,表达式总会得出有效数值且不存在除数为 0 的情况。
示例 1:
输入:tokens = ["2","1","+","3","*"] 输出:9 解释:该算式转化为常见的中缀算术表达式为:((2 + 1) * 3) = 9
示例 2:
输入:tokens = ["4","13","5","/","+"] 输出:6 解释:该算式转化为常见的中缀算术表达式为:(4 + (13 / 5)) = 6
示例 3:
输入:tokens = ["10","6","9","3","+","-11","*","/","*","17","+","5","+"] 输出:22 解释: 该算式转化为常见的中缀算术表达式为: ((10 * (6 / ((9 + 3) * -11))) + 17) + 5 = ((10 * (6 / (12 * -11))) + 17) + 5 = ((10 * (6 / -132)) + 17) + 5 = ((10 * 0) + 17) + 5 = (0 + 17) + 5 = 17 + 5 = 22
提示:
1 <= tokens.length <= 104tokens[i]要么是一个算符("+"、"-"、"*"或"/"),要么是一个在范围[-200, 200]内的整数
逆波兰表达式:
逆波兰表达式是一种后缀表达式,所谓后缀就是指算符写在后面。
- 平常使用的算式则是一种中缀表达式,如
( 1 + 2 ) * ( 3 + 4 )。 - 该算式的逆波兰表达式写法为
( ( 1 2 + ) ( 3 4 + ) * )。
逆波兰表达式主要有以下两个优点:
- 去掉括号后表达式无歧义,上式即便写成
1 2 + 3 4 + *也可以依据次序计算出正确结果。 - 适合用栈操作运算:遇到数字则入栈;遇到算符则取出栈顶两个数字进行计算,并将结果压入栈中。
class Solution {
public:
int evalRPN(vector<string>& tokens)
{
map<string,function<int(int,int)>> opFuncMap={
{"+",[](int x,int y){return x+y;}},
{"-",[](int x,int y){return x-y;}},
{"*",[](int x,int y){return x*y;}},
{"/",[](int x,int y){return x/y;}}
};
stack<int> st;
for(auto& str :tokens)
{
if(opFuncMap.count(str))
{
int right=st.top();
st.pop();
int left=st.top();
st.pop();
st.push(opFuncMap[str](left,right));
}
else//操作数入栈
{
st.push(stoi(str));
}
}
return st.top();
}
};这里就可以通过function来对应不同的操作符进行包装从而将不同的lambda函数进行包装,然后和相对应的操作符放入map中。然后从头遍历字符串,如果是数字类的char就存入栈中,如果是操作符就将栈顶的两个数进行操作符所对应的运算,然后重新放入栈中,直到字符串遍历完栈内存放的数就是最后的结果。