🪐🪐🪐欢迎来到程序员餐厅💫💫💫
主厨:邪王真眼
主厨的主页:Chef‘s blog
所属专栏:c++大冒险
总有光环在陨落,总有新星在闪烁
前言:
我们之前学习了哈希表,哈希表通过映射关系,实现了O(1)的复杂度来查找数据,哈希在实践中是一个非常重要的思想,今天要学习的就是哈希思想的两大应用:位图与布隆过滤器
一、 位图
1.1 面试题【腾讯】
给 40 亿个不重复的无符号整数,没排过序。给一个无符号整数,如何快速判断一个数是否在这40亿个数中。
- 1. 直接遍历,时间复杂度O(N)
- 2. 先排序(O(NlogN)),在利用二分查找: logN
- 3.二叉搜索树、map、set、哈希.......
但是不要忽略了一个问题:40亿个整型,存入内存就是大约16G,而且还会有别的内存开销(例如红黑树),所以上述方法是不现实的。
我们仔细想想,对于这道题目而言,一个数据只有两种状态:在/不在。如果我们想要标识两种状态,其实只需要一个比特位就够了,0表示不存在,1表示存在。通过哈希的映射思想,我们可以把每一个数据映射到一个比特位中,这就是位图的概念。
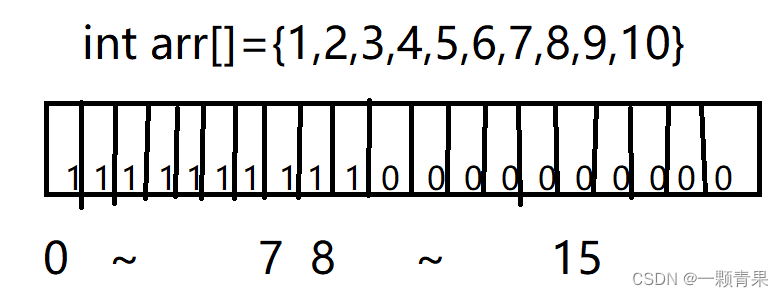
在STL库中,已经为我们提供了位图bitset,我先简单讲解一下bitset的接口,再给大家实现一个位图。

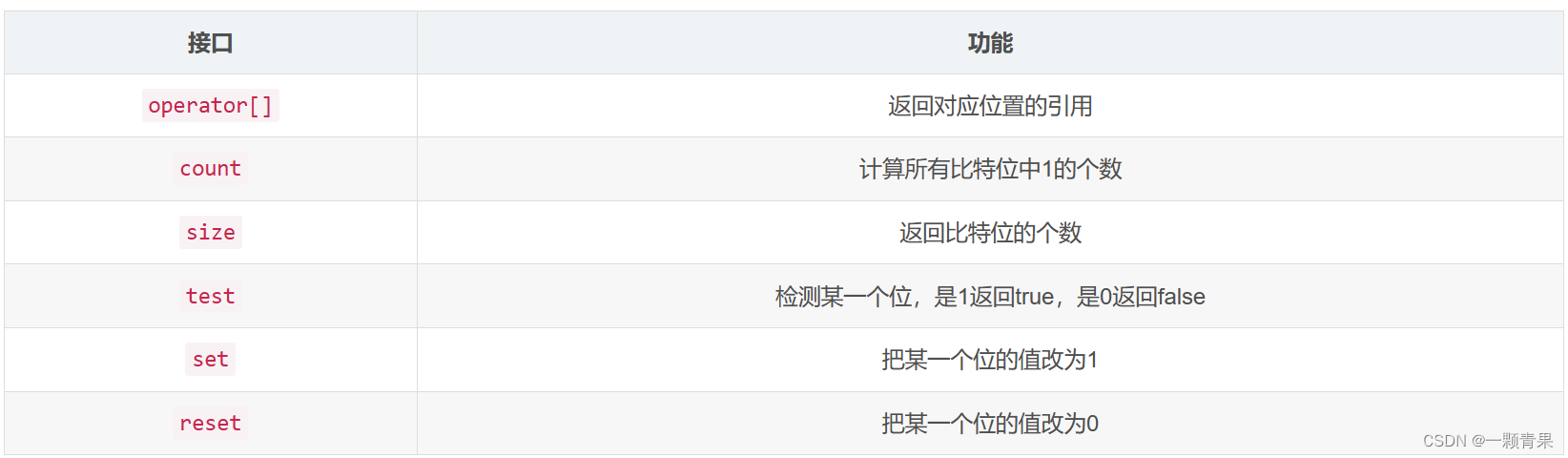
1.2位图的实现
1.2.1成员变量
template<size_t N>
class bitset
{
public:
protected:
vector<int> _bits;
};注意事项:
- 注意这个非类型模板参数
N,他其代表位图中要开多少个比特位,而不是字节!!!
1.2.3构造函数
思路:
我们先开一个数据类型是int的vector对象,一个int包含32比特位,接着直接对把数据的存在/不存在两种状态存放在对应比特位中,c++的除法是向下取整,所以要开(N/32+1)个int
BitSet()
{
_bits.resize(N /32 + 1);
}1.2.4set:
作用:把目标比特位的值改为1
现在传过来一个整数i,我们怎么找到它所对应的比特为呢?其实思路类似于一维数组转二维数组
i/32得到的是该比特位位于vector对象的的几个元素中,i%32得到的是该比特位处于当前元素的第几个比特位中。
size_t i = x / 32; // vector的第i个元素
size_t j = x % 32; // 第i个元素的第j个比特位
但是c++并没有直接修改目标比特位的函数,所以我们要还要思考怎么实现这个功能
这就要用到位移操作符了
我们要把整数i第j个比特位修改为1,可以先把1左移j位得到整数y,在把i与y按位或,注意我们比特位的计算是从0开始的,即一个整型比特位是0到31.
1000100 //待修改数据,把第3位修改为1
00000001 //数字1
00001000 //数字1左移3位
------------
10000100
00001000 //按位或
------------
10001100//得到结果set函数接口如下:
void set(size_t x)
{
assert(x <= N);//别忘了断言
int i = x / 32;
int j = x % 32;
_bits[i] |=1 << j;
}1.2.5reset:
作用:把目标比特位的值改为0
思路类似set:
我们要把整数x第i个比特位修改为0,可以先把1左移i位得到y,在把y二进制按位取反,最后x和y按位与,注意我们比特位的计算是从0开始的
void reset(size_t x)
{
assert(x <= N);//别忘了断言
int i = x / 32;
int j = x % 32;
_bits[i] &= ~(1 << j);
}1.2.6test:
作用:检测指定比特位的值是0还是1。
思路:
我们要检测整数x第i个比特位是1还是0,可以先把1左移i位得到y,在把y和x按位与,看结果是1还是0,并将其返回
bool test(size_t N)
{
assert(x <= N);
int i = x / 32;
int j = x % 32;
return _bits[i] & (1 << j);
}ps:其他接口实现简单,我们就不再赘述
1.3位图的应用
位图在处理大量数据时,有非常明显的优势,其主要功能如下:
- 以极低的内存消耗标识一个数据的状态(在/不在)
- 以O(1)的复杂度查找一个数据的状态
- 排序 + 去重
题目一
1个文件有100亿个int,1G内存,设法找到出现次数不超过2次的所有整数。
这种问题很明显就是利用位图来解决,可是前面的问题我们用了一个比特位标识出一个数字在/不在的两种状态。
那么这个问题呢?
我们可以设想为3种状态,出现0次、出现1次、出现2次、出现3次及以上,分别用如下数字标识:
出现0次:00
出现1次:01
出现2次:10
出现3次及以上:11
这样的位图每个数据就要用到两个比特的空间了,那我们要重新写一份吗?
NO!
我选择前人栽树后人乘凉:
template<size_t N>
class twobitset
{
public:
twobitset()
{
bs1(N);
bs2(N);
}
void set(size_t x)
{
//00->01
if (bs1.test(x) == false && bs2.test(x) == false)
bs2.set(x);
//01->10
else if (bs1.test(x) == false && bs2.test(x))
{
bs1.set(x);
bs2.reset(x);
}
//10->11及以上
else
{
bs2.set(x);
}
}
int test(size_t x)
{
if (bs1.test(x) == false && bs2.test(x) == false)
return 0;
//01->10
else if (bs1.test(x) == false && bs2.test(x))
{
return 1;
}
//10->11及以上
else if (bs1.test(x) && bs2.test(x) == false)
{
return 2;
}
else
return 3;
}
protected:
bitset<N> bs1;
bitset<N> bs2;
}; 题目二:
给两个文件,分别有100亿个整数(unsigned int),我们只有1G内存,如何找到两个文件的交集?
一个文件的大小大约就在40G,不可能放进内存中直接比较的,因此我们可以考虑位图,我们要开42亿个比特位。大概也就是0.5G。
我们分别把两个文件的数据分别插入到两个位图中,此时我们就有两个范围是0 - 42亿数的位图了,总共也就是1G。然后我们同时再遍历两个位图,分别对比每一个位,只要两张位图该比特位都是1,那就是文件的交集,把值存到其中一张位图中(别再开vector了,咋没空间了),最后销毁其中一个位图,把交集放到新建的vector中并返回。
二、布隆过滤器
2.1 布隆过滤器提出
- 1. 用哈希表存储用户记录,缺点:浪费空间
- 2. 用位图存储用户记录,缺点:位图一般只能处理整形,如果内容编号是字符串,就无法处理 了。
- 3. 将哈希与位图结合,即布隆过滤器
2.2布隆过滤器概念
"C语言""C++""C#""Java""go to"
我们一一通过哈希函数把他们映射到vector的某一个比特位中,这时候就可能发生哈希冲突,数值之间相互覆盖
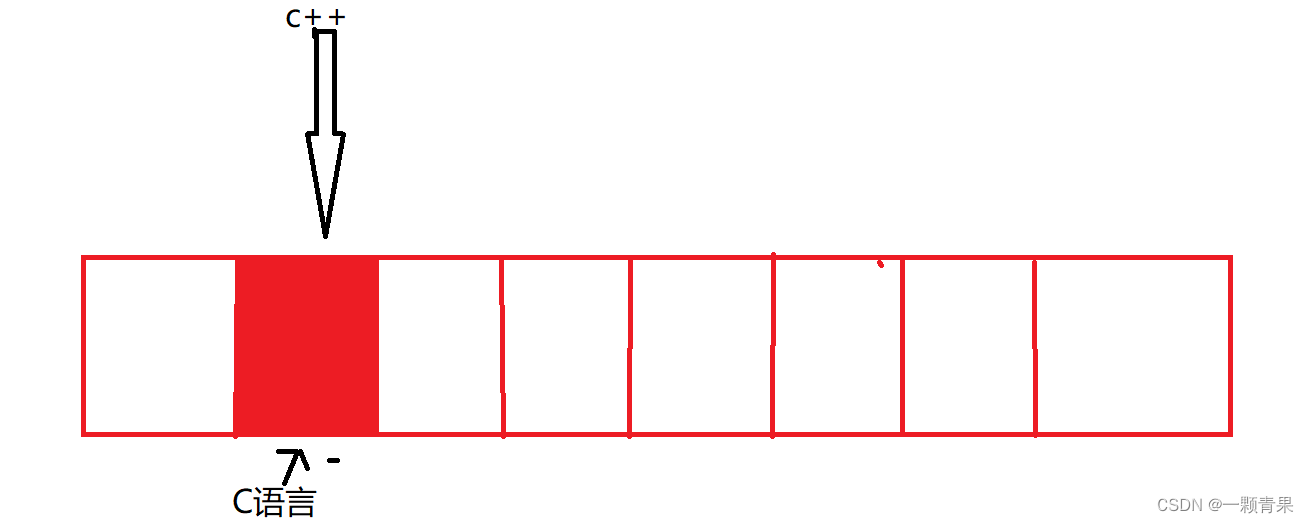
那我们该怎么降低误差呢?
把一个数据通过三套不同的哈希函数,映射到三个比特位上
降低误差的原理:
插入元素时,我们会把它所对应的三个比特位都修改为1,而在检查某元素是否存在时,只有这三个比特位值都为1时才认为该数据存在,所以如果只是一两个比特位发生冲突那也不会影响结果,当该数据的三个比特位都发生哈希冲突才会产生识别存在与否错误(这就是布隆过滤器误差来源) 。因此降低了误差,理论上你设定的1个数据用n个比特位存储,n越大,误差越小,但占用空间也更多。
相互不影响状态:

发生哈希冲突但不会产生错误:
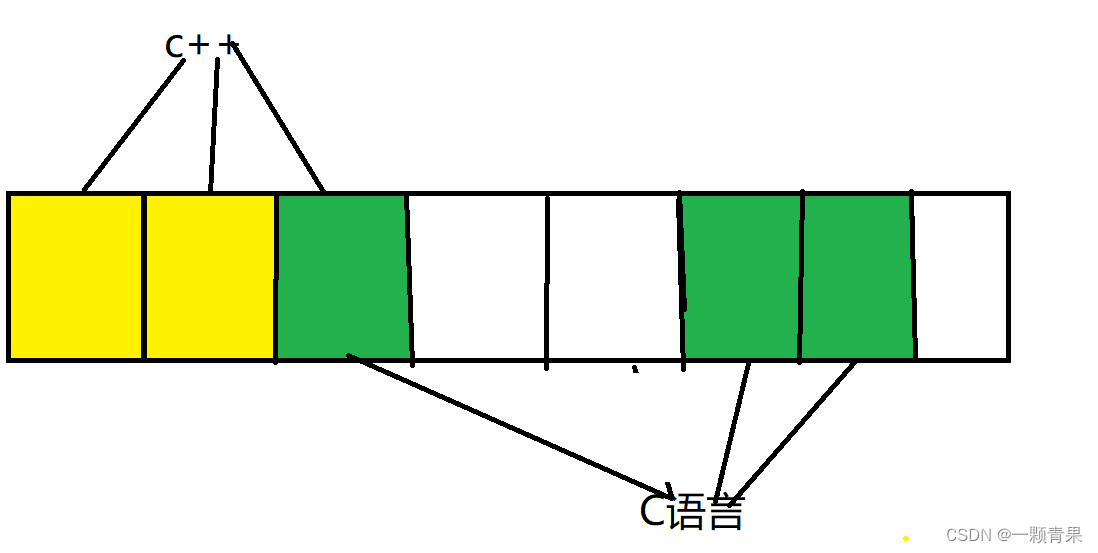
当我们查找数据的时候,只有这个数据上的三个比特位都为1,才说明这个数据存在。
2 .3布隆过滤器的实现
2.3.1成员变量:
template<size_t N, class K = string, class HF1 = HashFuncAP, class HF2 = HashFuncBKDR, class HF3 = HashFuncDJB>
class BloomFilter
{
public:
protected:
bitset<5 * N> _bs;
}要点洞悉:
- 模板参数是什么
布隆过滤器有五个模板参数,N代表要插入的数据个数,K代表要处理的类型,剩下三个是不同的哈希函数,用于映射不同的比特位。
- 哈希函数怎么选
我们需要实现三个哈希函数,这里我们使用BKDR、AP、DJB三种,为什么这么写是有讲究的,涉及到了数学原理,感兴趣的朋友可以去看看这篇文章哈希函数的选择
struct HashFuncBKDR
{
size_t operator()(const string& s)
{
size_t hash = 0;
for (auto ch : s)
{
hash += ch;
hash *= 131;
}
return hash;
}
};
struct HashFuncAP
{
size_t operator()(const string& s)
{
size_t hash = 0;
int i;
for (i = 0; i < s.size(); i++)
{
if ((i & 1) == 0)// 偶数位字符
hash ^= ((hash << 7) ^ (s[i]) ^ (hash >> 3));
else//奇数位字符
hash ^= (~((hash << 11) ^ (s[i]) ^ (hash >> 5)));
}
return hash;
}
};
struct HashFuncDJB
{
size_t operator()(const string& s)
{
register size_t hash = 5381;
for (auto ch : s)
hash = hash * 33 ^ ch;
return hash;
}
};- 为什么是设计的vector传参是5*N
知乎有大佬经过计算得到如下图这样的结论:
在选择布隆过滤器的长度和哈希函数的数量时应满足下图公式

知乎文章在此:布隆过滤器详解
与此我们直到当选择了三个哈希函数时,布隆过滤器的长度应是(N*3/ln 2),向上取整得5
因此有bitset<5 * N> _bs;
2.3.2插入set
想要插入一个 数据,其实就是通过三个哈希函数计算出三个映射位置,并把它们设置为1。
void set(const K& key)
{
size_t hash1=(HF1()(key))%(5*N);
size_t hash2 = (HF2()(key)) % (5 * N);
size_t hash3 = (HF3()(key)) % (5 * N);
_bs.set(hash1);
_bs.set(hash2);
_bs.set(hash3);
}2.3.3查找test
bool test(const& K key)
{
size_t hash1 = (HF1()(key)) % (5 * N);
size_t hash2 = (HF2()(key)) % (5 * N);
size_t hash3 = (HF3()(key)) % (5 * N);
return _bs.test(hash1)&&_bs.test(hash2)&&_bs.test(hash3);
}2.3.4删除reset

2.4 布隆过滤器优点
- 1. 增加和查询元素的时间复杂度为:O(K), (K为哈希函数的个数,一般比较小),与数据量大小无关
- 2. 哈希函数相互之间没有关系,方便硬件并行运算
- 3. 布隆过滤器不需要存储元素本身,在某些对保密要求比较严格的场合有很大优势
- 4. 在能够承受一定的误判时,布隆过滤器比其他数据结构有这很大的空间优势
- 5. 数据量很大时,布隆过滤器可以表示全集,其他数据结构不能
- 6. 使用同一组散列函数的布隆过滤器可以进行交、并、差运算
2.5 布隆过滤器缺陷
- 1. 有误判率,即存在假阳性(False Position),即不能准确判断元素是否在集合中(补救方法:再建立一个白名单,存储可能会误判的数据)
- 2. 不能获取元素本身
- 3. 一般情况下不能从布隆过滤器中删除元素
- 4. 如果采用计数方式删除,可能会存在计数回绕问题
2.6布隆过滤器使用场景:
小明买了手机,去注册手机号,选了一个号码
1.把号码输入布隆过滤器,接受返回值
2.返回值是假,说明该号码没被用过
3.返回值是真,说明该号码可能用过,则再去数据库中寻找看是否用过
🥰创作不易,你的支持对我最大的鼓励🥰
🪐~ 点赞收藏+关注 ~🪐