下载APP
12 | 排序(下):如何用快排思想在O(n)内查找第K大元素?
2018-10-17 王争数据结构与算法之美进入课程
![]()
![]()
![]()
![]()
讲述:修阳
时长21:58大小8.81M
上一节我讲了冒泡排序、插入排序、选择排序这三种排序算法,它们的时间复杂度都是 O(n2),比较高,适合小规模数据的排序。今天,我讲两种时间复杂度为 O(nlogn) 的排序算法,归并排序和快速排序。这两种排序算法适合大规模的数据排序,比上一节讲的那三种排序算法要更常用。
归并排序和快速排序都用到了分治思想,非常巧妙。我们可以借鉴这个思想,来解决非排序的问题,比如:如何在 O(n) 的时间复杂度内查找一个无序数组中的第 K 大元素? 这就要用到我们今天要讲的内容。
归并排序的原理
我们先来看归并排序(Merge Sort)。
归并排序的核心思想还是蛮简单的。如果要排序一个数组,我们先把数组从中间分成前后两部分,然后对前后两部分分别排序,再将排好序的两部分合并在一起,这样整个数组就都有序了。

归并排序使用的就是分治思想。分治,顾名思义,就是分而治之,将一个大问题分解成小的子问题来解决。小的子问题解决了,大问题也就解决了。
从我刚才的描述,你有没有感觉到,分治思想跟我们前面讲的递归思想很像。是的,分治算法一般都是用递归来实现的。分治是一种解决问题的处理思想,递归是一种编程技巧,这两者并不冲突。分治算法的思想我后面会有专门的一节来讲,现在不展开讨论,我们今天的重点还是排序算法。
前面我通过举例让你对归并有了一个感性的认识,又告诉你,归并排序用的是分治思想,可以用递归来实现。我们现在就来看看如何用递归代码来实现归并排序。
我在第 10 节讲的递归代码的编写技巧你还记得吗?写递归代码的技巧就是,分析得出递推公式,然后找到终止条件,最后将递推公式翻译成递归代码。所以,要想写出归并排序的代码,我们先写出归并排序的递推公式。
|
| |
|
| |
|
| |
|
|
复制代码
我来解释一下这个递推公式。
merge_sort(p…r) 表示,给下标从 p 到 r 之间的数组排序。我们将这个排序问题转化为了两个子问题,merge_sort(p…q) 和 merge_sort(q+1…r),其中下标 q 等于 p 和 r 的中间位置,也就是 (p+r)/2。当下标从 p 到 q 和从 q+1 到 r 这两个子数组都排好序之后,我们再将两个有序的子数组合并在一起,这样下标从 p 到 r 之间的数据就也排好序了。
有了递推公式,转化成代码就简单多了。为了阅读方便,我这里只给出伪代码,你可以翻译成你熟悉的编程语言。
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
|
|
复制代码
你可能已经发现了,merge(A[p…r], A[p…q], A[q+1…r]) 这个函数的作用就是,将已经有序的 A[p…q] 和 A[q+1…r] 合并成一个有序的数组,并且放入 A[p…r]。那这个过程具体该如何做呢?
如图所示,我们申请一个临时数组 tmp,大小与 A[p…r] 相同。我们用两个游标 i 和 j,分别指向 A[p…q] 和 A[q+1…r] 的第一个元素。比较这两个元素 A[i] 和 A[j],如果 A[i]<=A[j],我们就把 A[i] 放入到临时数组 tmp,并且 i 后移一位,否则将 A[j] 放入到数组 tmp,j 后移一位。
继续上述比较过程,直到其中一个子数组中的所有数据都放入临时数组中,再把另一个数组中的数据依次加入到临时数组的末尾,这个时候,临时数组中存储的就是两个子数组合并之后的结果了。最后再把临时数组 tmp 中的数据拷贝到原数组 A[p…r] 中。
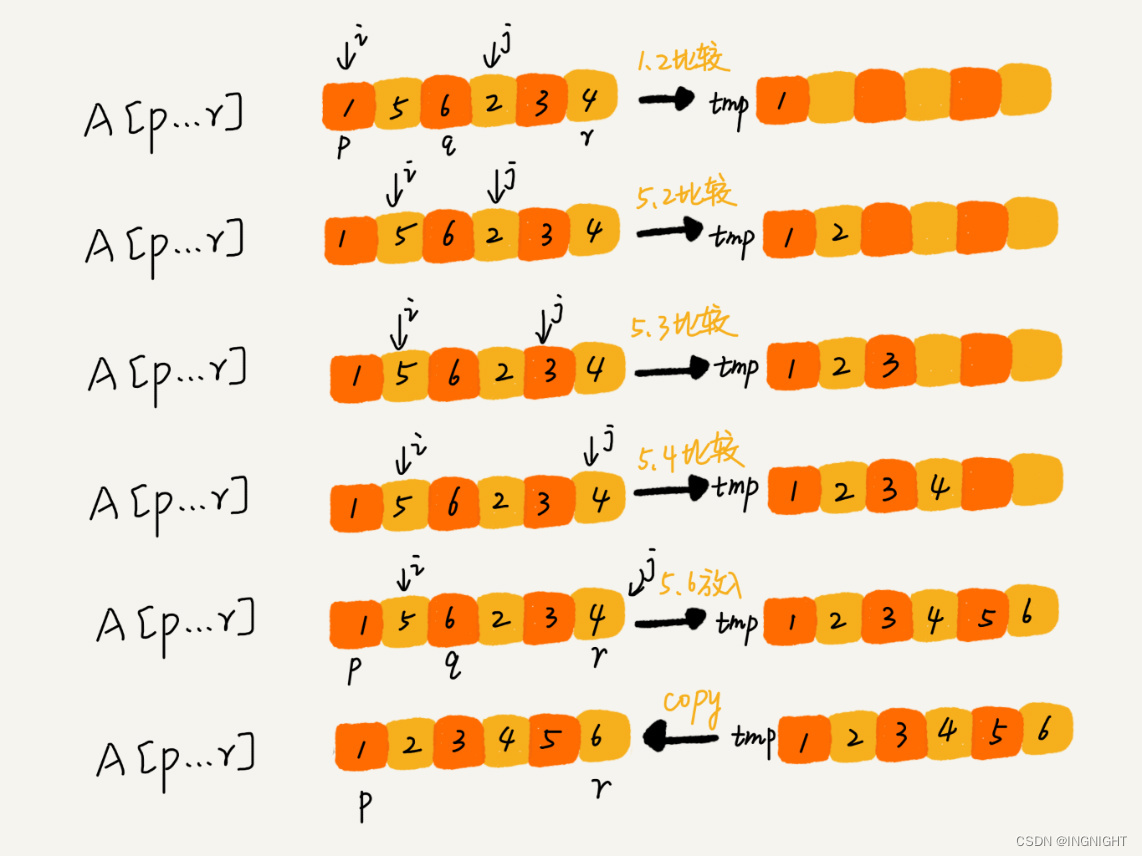
我们把 merge() 函数写成伪代码,就是下面这样:
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
|
|
复制代码
你还记得第 7 讲讲过的利用哨兵简化编程的处理技巧吗?merge() 合并函数如果借助哨兵,代码就会简洁很多,这个问题留给你思考。
归并排序的性能分析
这样跟着我一步一步分析,归并排序是不是没那么难啦?还记得上节课我们分析排序算法的三个问题吗?接下来,我们来看归并排序的三个问题。
第一,归并排序是稳定的排序算法吗?
结合我前面画的那张图和归并排序的伪代码,你应该能发现,归并排序稳不稳定关键要看 merge() 函数,也就是两个有序子数组合并成一个有序数组的那部分代码。
在合并的过程中,如果 A[p…q] 和 A[q+1…r] 之间有值相同的元素,那我们可以像伪代码中那样,先把 A[p…q] 中的元素放入 tmp 数组。这样就保证了值相同的元素,在合并前后的先后顺序不变。所以,归并排序是一个稳定的排序算法。
第二,归并排序的时间复杂度是多少?
归并排序涉及递归,时间复杂度的分析稍微有点复杂。我们正好借此机会来学习一下,如何分析递归代码的时间复杂度。
在递归那一节我们讲过,递归的适用场景是,一个问题 a 可以分解为多个子问题 b、c,那求解问题 a 就可以分解为求解问题 b、c。问题 b、c 解决之后,我们再把 b、c 的结果合并成 a 的结果。
如果我们定义求解问题 a 的时间是 T(a),求解问题 b、c 的时间分别是 T(b) 和 T( c),那我们就可以得到这样的递推关系式:
|
|
复制代码
其中 K 等于将两个子问题 b、c 的结果合并成问题 a 的结果所消耗的时间。
从刚刚的分析,我们可以得到一个重要的结论:不仅递归求解的问题可以写成递推公式,递归代码的时间复杂度也可以写成递推公式。
套用这个公式,我们来分析一下归并排序的时间复杂度。
我们假设对 n 个元素进行归并排序需要的时间是 T(n),那分解成两个子数组排序的时间都是 T(n/2)。我们知道,merge() 函数合并两个有序子数组的时间复杂度是 O(n)。所以,套用前面的公式,归并排序的时间复杂度的计算公式就是:
|
| |
|
|
复制代码
通过这个公式,如何来求解 T(n) 呢?还不够直观?那我们再进一步分解一下计算过程。
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
|
|
复制代码
通过这样一步一步分解推导,我们可以得到 T(n) = 2^kT(n/2^k)+kn。当 T(n/2^k)=T(1) 时,也就是 n/2^k=1,我们得到 k=log2n 。我们将 k 值代入上面的公式,得到 T(n)=Cn+nlog2n 。如果我们用大 O 标记法来表示的话,T(n) 就等于 O(nlogn)。所以归并排序的时间复杂度是 O(nlogn)。
从我们的原理分析和伪代码可以看出,归并排序的执行效率与要排序的原始数组的有序程度无关,所以其时间复杂度是非常稳定的,不管是最好情况、最坏情况,还是平均情况,时间复杂度都是 O(nlogn)。
第三,归并排序的空间复杂度是多少?
归并排序的时间复杂度任何情况下都是 O(nlogn),看起来非常优秀。(待会儿你会发现,即便是快速排序,最坏情况下,时间复杂度也是 O(n2)。)但是,归并排序并没有像快排那样,应用广泛,这是为什么呢?因为它有一个致命的“弱点”,那就是归并排序不是原地排序算法。
这是因为归并排序的合并函数,在合并两个有序数组为一个有序数组时,需要借助额外的存储空间。这一点你应该很容易理解。那我现在问你,归并排序的空间复杂度到底是多少呢?是 O(n),还是 O(nlogn),应该如何分析呢?
如果我们继续按照分析递归时间复杂度的方法,通过递推公式来求解,那整个归并过程需要的空间复杂度就是 O(nlogn)。不过,类似分析时间复杂度那样来分析空间复杂度,这个思路对吗?
实际上,递归代码的空间复杂度并不能像时间复杂度那样累加。刚刚我们忘记了最重要的一点,那就是,尽管每次合并操作都需要申请额外的内存空间,但在合并完成之后,临时开辟的内存空间就被释放掉了。在任意时刻,CPU 只会有一个函数在执行,也就只会有一个临时的内存空间在使用。临时内存空间最大也不会超过 n 个数据的大小,所以空间复杂度是 O(n)。
快速排序的原理
我们再来看快速排序算法(Quicksort),我们习惯性把它简称为“快排”。快排利用的也是分治思想。乍看起来,它有点像归并排序,但是思路其实完全不一样。我们待会会讲两者的区别。现在,我们先来看下快排的核心思想。
快排的思想是这样的:如果要排序数组中下标从 p 到 r 之间的一组数据,我们选择 p 到 r 之间的任意一个数据作为 pivot(分区点)。
我们遍历 p 到 r 之间的数据,将小于 pivot 的放到左边,将大于 pivot 的放到右边,将 pivot 放到中间。经过这一步骤之后,数组 p 到 r 之间的数据就被分成了三个部分,前面 p 到 q-1 之间都是小于 pivot 的,中间是 pivot,后面的 q+1 到 r 之间是大于 pivot 的。
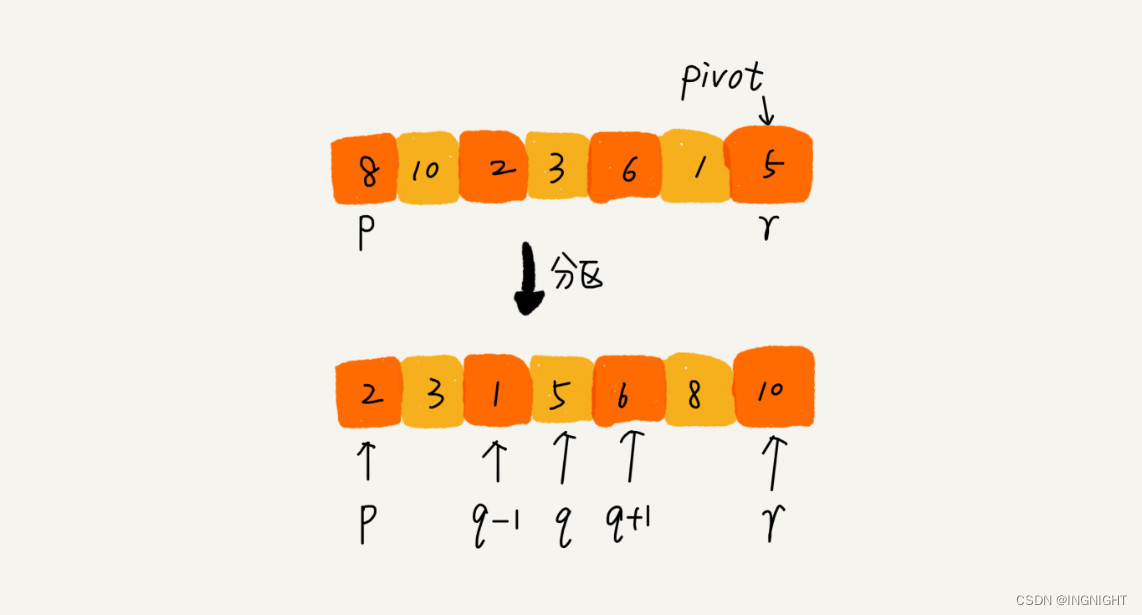
根据分治、递归的处理思想,我们可以用递归排序下标从 p 到 q-1 之间的数据和下标从 q+1 到 r 之间的数据,直到区间缩小为 1,就说明所有的数据都有序了。
如果我们用递推公式来将上面的过程写出来的话,就是这样:
|
| |
|
| |
|
| |
|
|
复制代码
我将递推公式转化成递归代码。跟归并排序一样,我还是用伪代码来实现,你可以翻译成你熟悉的任何语言。
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
|
|
复制代码
归并排序中有一个 merge() 合并函数,我们这里有一个 partition() 分区函数。partition() 分区函数实际上我们前面已经讲过了,就是随机选择一个元素作为 pivot(一般情况下,可以选择 p 到 r 区间的最后一个元素),然后对 A[p…r] 分区,函数返回 pivot 的下标。
如果我们不考虑空间消耗的话,partition() 分区函数可以写得非常简单。我们申请两个临时数组 X 和 Y,遍历 A[p…r],将小于 pivot 的元素都拷贝到临时数组 X,将大于 pivot 的元素都拷贝到临时数组 Y,最后再将数组 X 和数组 Y 中数据顺序拷贝到 A[p…r]。
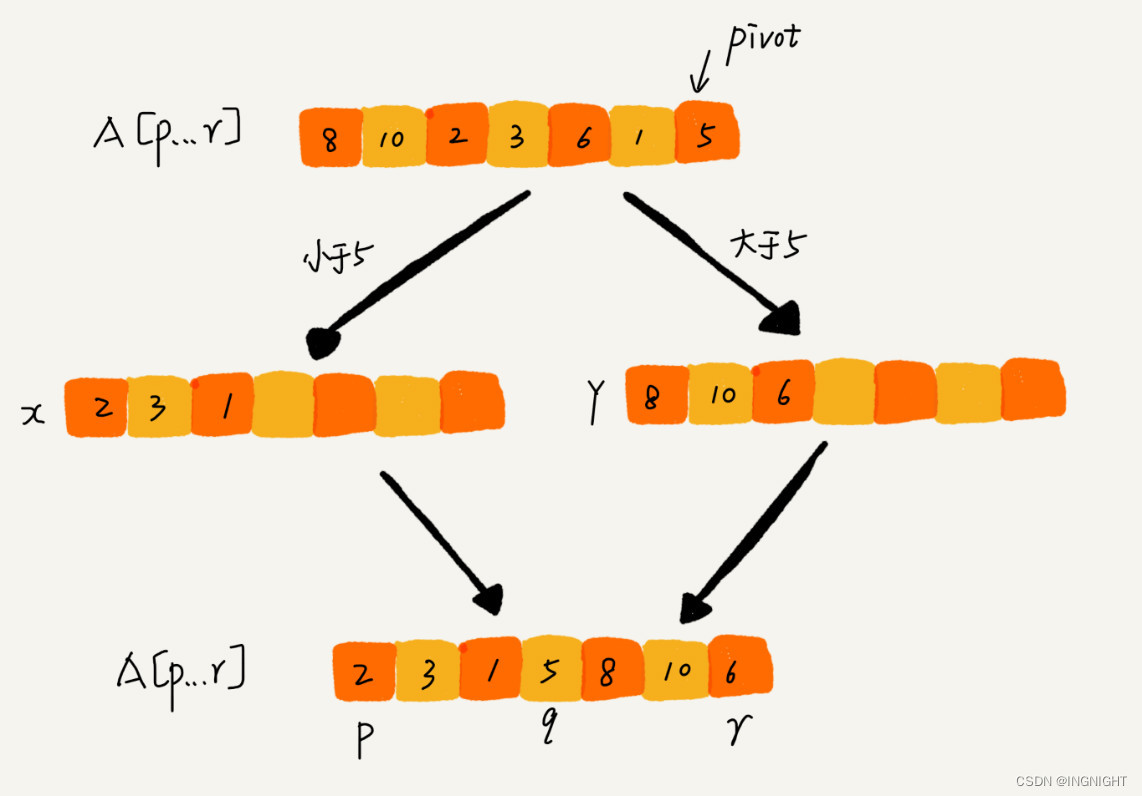
但是,如果按照这种思路实现的话,partition() 函数就需要很多额外的内存空间,所以快排就不是原地排序算法了。如果我们希望快排是原地排序算法,那它的空间复杂度得是 O(1),那 partition() 分区函数就不能占用太多额外的内存空间,我们就需要在 A[p…r] 的原地完成分区操作。
原地分区函数的实现思路非常巧妙,我写成了伪代码,我们一起来看一下。
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
复制代码
这里的处理有点类似选择排序。我们通过游标 i 把 A[p…r-1] 分成两部分。A[p…i-1] 的元素都是小于 pivot 的,我们暂且叫它“已处理区间”,A[i…r-1] 是“未处理区间”。我们每次都从未处理的区间 A[i…r-1] 中取一个元素 A[j],与 pivot 对比,如果小于 pivot,则将其加入到已处理区间的尾部,也就是 A[i] 的位置。
数组的插入操作还记得吗?在数组某个位置插入元素,需要搬移数据,非常耗时。当时我们也讲了一种处理技巧,就是交换,在 O(1) 的时间复杂度内完成插入操作。这里我们也借助这个思想,只需要将 A[i] 与 A[j] 交换,就可以在 O(1) 时间复杂度内将 A[j] 放到下标为 i 的位置。
文字不如图直观,所以我画了一张图来展示分区的整个过程。
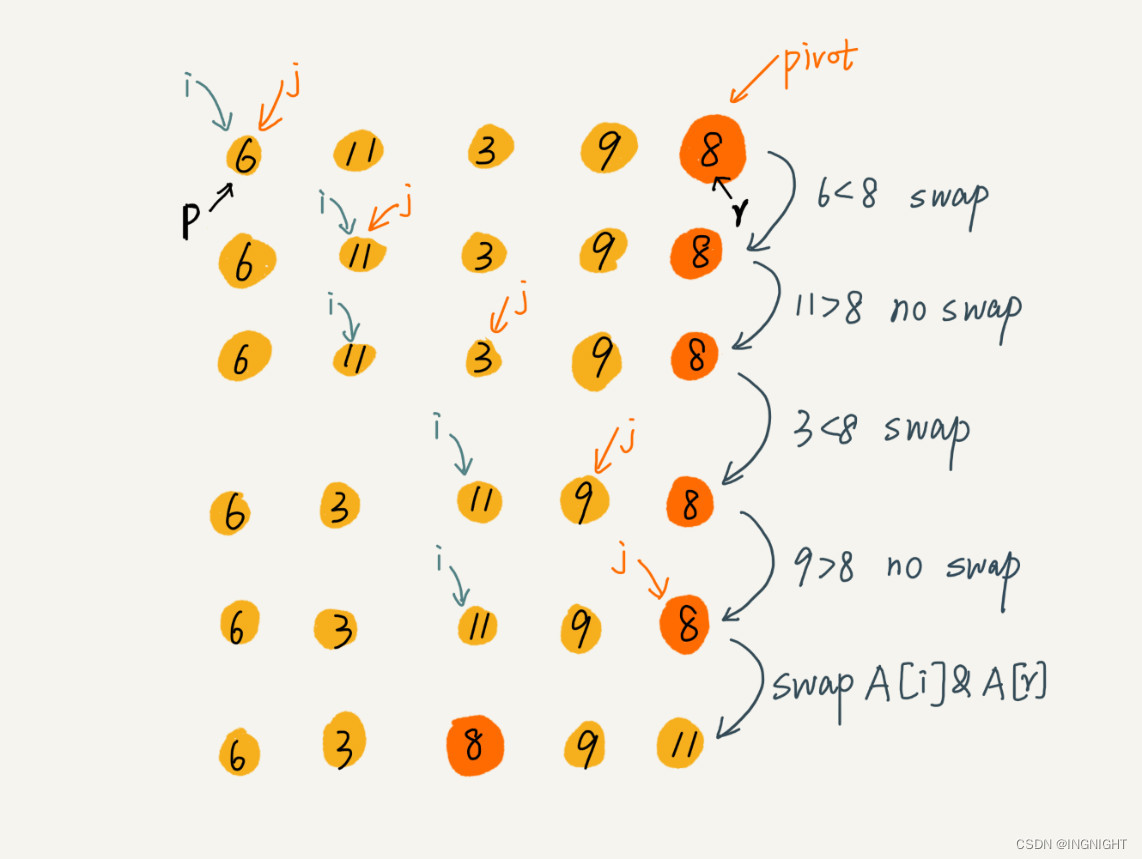
因为分区的过程涉及交换操作,如果数组中有两个相同的元素,比如序列 6,8,7,6,3,5,9,4,在经过第一次分区操作之后,两个 6 的相对先后顺序就会改变。所以,快速排序并不是一个稳定的排序算法。
到此,快速排序的原理你应该也掌握了。现在,我再来看另外一个问题:快排和归并用的都是分治思想,递推公式和递归代码也非常相似,那它们的区别在哪里呢?
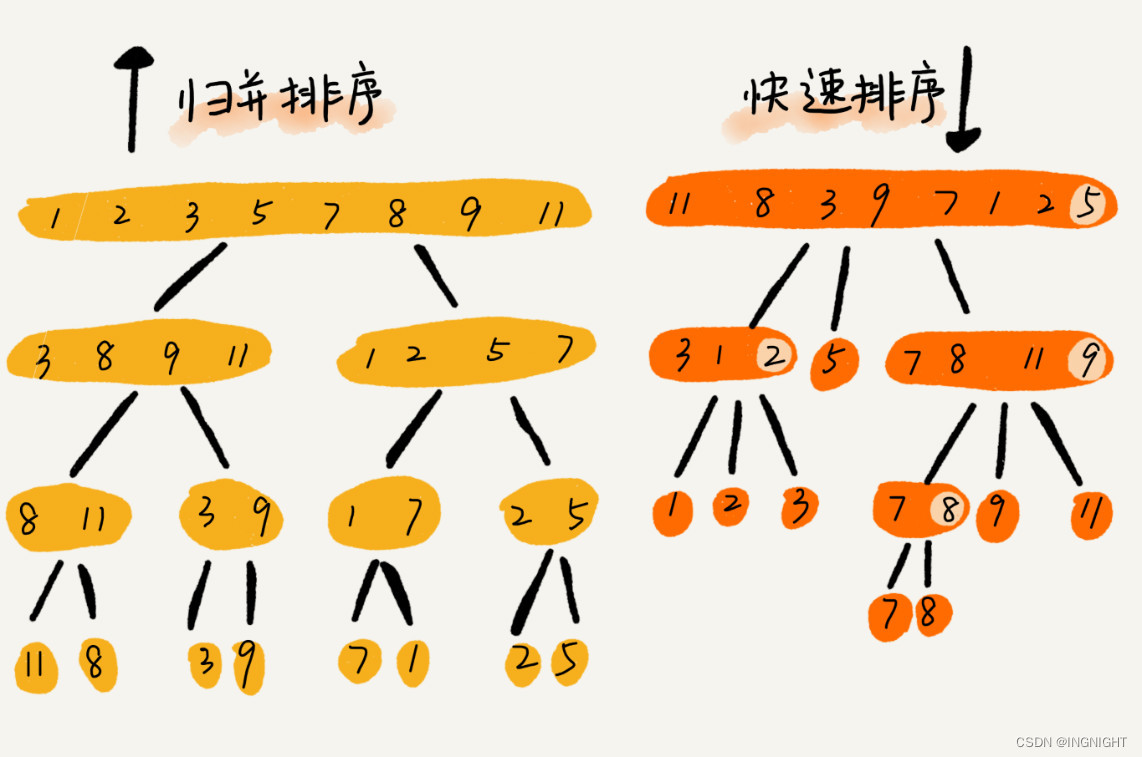
可以发现,归并排序的处理过程是由下到上的,先处理子问题,然后再合并。而快排正好相反,它的处理过程是由上到下的,先分区,然后再处理子问题。归并排序虽然是稳定的、时间复杂度为 O(nlogn) 的排序算法,但是它是非原地排序算法。我们前面讲过,归并之所以是非原地排序算法,主要原因是合并函数无法在原地执行。快速排序通过设计巧妙的原地分区函数,可以实现原地排序,解决了归并排序占用太多内存的问题。
快速排序的性能分析
现在,我们来分析一下快速排序的性能。我在讲解快排的实现原理的时候,已经分析了稳定性和空间复杂度。快排是一种原地、不稳定的排序算法。现在,我们集中精力来看快排的时间复杂度。
快排也是用递归来实现的。对于递归代码的时间复杂度,我前面总结的公式,这里也还是适用的。如果每次分区操作,都能正好把数组分成大小接近相等的两个小区间,那快排的时间复杂度递推求解公式跟归并是相同的。所以,快排的时间复杂度也是 O(nlogn)。
|
| |
|
|
复制代码
但是,公式成立的前提是每次分区操作,我们选择的 pivot 都很合适,正好能将大区间对等地一分为二。但实际上这种情况是很难实现的。
我举一个比较极端的例子。如果数组中的数据原来已经是有序的了,比如 1,3,5,6,8。如果我们每次选择最后一个元素作为 pivot,那每次分区得到的两个区间都是不均等的。我们需要进行大约 n 次分区操作,才能完成快排的整个过程。每次分区我们平均要扫描大约 n/2 个元素,这种情况下,快排的时间复杂度就从 O(nlogn) 退化成了 O(n2)。
我们刚刚讲了两个极端情况下的时间复杂度,一个是分区极其均衡,一个是分区极其不均衡。它们分别对应快排的最好情况时间复杂度和最坏情况时间复杂度。那快排的平均情况时间复杂度是多少呢?
我们假设每次分区操作都将区间分成大小为 9:1 的两个小区间。我们继续套用递归时间复杂度的递推公式,就会变成这样:
|
| |
|
|
复制代码
这个公式的递推求解的过程非常复杂,虽然可以求解,但我不推荐用这种方法。实际上,递归的时间复杂度的求解方法除了递推公式之外,还有递归树,在树那一节我再讲,这里暂时不说。我这里直接给你结论:T(n) 在大部分情况下的时间复杂度都可以做到 O(nlogn),只有在极端情况下,才会退化到 O(n2)。而且,我们也有很多方法将这个概率降到很低,如何来做?我们后面章节再讲。
解答开篇
快排核心思想就是分治和分区,我们可以利用分区的思想,来解答开篇的问题:O(n) 时间复杂度内求无序数组中的第 K 大元素。比如,4, 2, 5, 12, 3 这样一组数据,第 3 大元素就是 4。
我们选择数组区间 A[0…n-1] 的最后一个元素 A[n-1] 作为 pivot,对数组 A[0…n-1] 原地分区,这样数组就分成了三部分,A[0…p-1]、A[p]、A[p+1…n-1]。
如果 p+1=K,那 A[p] 就是要求解的元素;如果 K>p+1, 说明第 K 大元素出现在 A[p+1…n-1] 区间,我们再按照上面的思路递归地在 A[p+1…n-1] 这个区间内查找。同理,如果 K<p+1,那我们就在 A[0…p-1] 区间查找。
我们再来看,为什么上述解决思路的时间复杂度是 O(n)?
第一次分区查找,我们需要对大小为 n 的数组执行分区操作,需要遍历 n 个元素。第二次分区查找,我们只需要对大小为 n/2 的数组执行分区操作,需要遍历 n/2 个元素。依次类推,分区遍历元素的个数分别为、n/2、n/4、n/8、n/16.……直到区间缩小为 1。
如果我们把每次分区遍历的元素个数加起来,就是:n+n/2+n/4+n/8+…+1。这是一个等比数列求和,最后的和等于 2n-1。所以,上述解决思路的时间复杂度就为 O(n)。
你可能会说,我有个很笨的办法,每次取数组中的最小值,将其移动到数组的最前面,然后在剩下的数组中继续找最小值,以此类推,执行 K 次,找到的数据不就是第 K 大元素了吗?
不过,时间复杂度就并不是 O(n) 了,而是 O(K * n)。你可能会说,时间复杂度前面的系数不是可以忽略吗?O(K * n) 不就等于 O(n) 吗?
这个可不能这么简单地划等号。当 K 是比较小的常量时,比如 1、2,那最好时间复杂度确实是 O(n);但当 K 等于 n/2 或者 n 时,这种最坏情况下的时间复杂度就是 O(n2) 了。
内容小结
归并排序和快速排序是两种稍微复杂的排序算法,它们用的都是分治的思想,代码都通过递归来实现,过程非常相似。理解归并排序的重点是理解递推公式和 merge() 合并函数。同理,理解快排的重点也是理解递推公式,还有 partition() 分区函数。
归并排序算法是一种在任何情况下时间复杂度都比较稳定的排序算法,这也使它存在致命的缺点,即归并排序不是原地排序算法,空间复杂度比较高,是 O(n)。正因为此,它也没有快排应用广泛。
快速排序算法虽然最坏情况下的时间复杂度是 O(n2),但是平均情况下时间复杂度都是 O(nlogn)。不仅如此,快速排序算法时间复杂度退化到 O(n2) 的概率非常小,我们可以通过合理地选择 pivot 来避免这种情况。
课后思考
现在你有 10 个接口访问日志文件,每个日志文件大小约 300MB,每个文件里的日志都是按照时间戳从小到大排序的。你希望将这 10 个较小的日志文件,合并为 1 个日志文件,合并之后的日志仍然按照时间戳从小到大排列。如果处理上述排序任务的机器内存只有 1GB,你有什么好的解决思路,能“快速”地将这 10 个日志文件合并吗?
欢迎留言和我分享,我会第一时间给你反馈。
我已将本节内容相关的详细代码更新到 GitHub,戳此即可查看。

© 版权归极客邦科技所有,未经许可不得传播售卖。 页面已增加防盗追踪,如有侵权极客邦将依法追究其法律责任。
上一篇
11 | 排序(上):为什么插入排序比冒泡排序更受欢迎?
下一篇
13 | 线性排序:如何根据年龄给100万用户数据排序?
写留言
精选留言(268)

峰 置顶
2018-10-17
54
每次从各个文件中取一条数据,在内存中根据数据时间戳构建一个最小堆,然后每次把最小值给写入新文件,同时将最小值来自的那个文件再出来一个数据,加入到最小堆中。这个空间复杂度为常数,但没能很好利用1g内存,而且磁盘单个读取比较慢,所以考虑每次读取一批数据,没了再从磁盘中取,时间复杂度还是一样O(n)。
展开

Light Lin
2018-10-17
222
伪代码反而看得费劲,可能还是对代码不够敏感吧
展开
作者回复: 那我以后还是写代码吧

你有资格吗...
2018-10-18
131
建议还是写源码吧,伪代码不能体现细节,基础不好的同学看起来也费劲,还有一个问题课后思考能不能在下一节课开头讲一下,因为感觉您每次留的课后思考都很精辟,想知道以您的维度怎么来思考和解决这个问题

李建辉
2018-10-28
116
先构建十条io流,分别指向十个文件,每条io流读取对应文件的第一条数据,然后比较时间戳,选择出时间戳最小的那条数据,将其写入一个新的文件,然后指向该时间戳的io流读取下一行数据,然后继续刚才的操作,比较选出最小的时间戳数据,写入新文件,io流读取下一行数据,以此类推,完成文件的合并, 这种处理方式,日志文件有n个数据就要比较n次,每次比较选出一条数据来写入,时间复杂度是O(n),空间复杂度是O(1),几乎不占用内存,这是我想出的认为最好的操作了,希望老师指出最佳的做法!!!
展开
作者回复: 你回答的不错 思路是正确的

王先统
2018-10-17
62
可以为每个文件分配一个40M的数组,再另外分配一个400M的数组储存归并结果,每个文件每次读取40M,对十个数组做归并排序直到其中某个数组的数据被处理完,这时将归并结果写入磁盘,处理完的数组继续读入40M继续参与归并,以此类推,直到所有文件都处理完
展开

侯金彪
2018-10-17
37
老师,有个问题没懂,在一个数组中找第k大的数这个问题中,为什么如果p+1=k,a[p]就是要查找的结果呢?
展开

www.xnsms...
2018-10-23
20
用java来写吧,估计这里90%都是java开发!伪代码看的蛋疼

周茜(Dian...
2018-10-26
19
看了十几节课,第一次留言竟然是支持老师写伪代码。捂脸。不希望被代表。另外希望总结的同学,尽量少写一点吧,翻着太累了。我也写总结,在自己的笔记应用里。默写。写完再查漏补缺。感觉效果很好,也能检查自己到底学进去多少。
展开

陈华应
2018-10-17
19
坚持初衷,死磕就行,不退缩,不放弃!
展开

曹源
2018-10-18
18
先取得十个文件时间戳的最小值数组的最小值a,和最大值数组的最大值b。然后取mid=(a+b)/2,然后把每个文件按照mid分割,取所有前面部分之和,如果小于1g就可以读入内存快排生成中间文件,否则继续取时间戳的中间值分割文件,直到区间内文件之和小于1g。同理对所有区间都做同样处理。最终把生成的中间文件按照分割的时间区间的次序直接连起来即可。
展开

我来也
2018-10-21
17
我觉得最后的思考题,[曹源]同学的策略是较优的。
该策略的最大好处是充分利用了内存。
但是我还是会这么做:
1.申请10个40M的数组和一个400M的数组。
2.每个文件都读40M,取各数组中最大时间戳中的最小值。
3.然后利用二分查找,在其他数组中快速定位到小于/等于该时间戳的位置,并做标记。
4.再把各数组中标记位置之前的数据全部放在申请的400M内存中,
5.在原来的40M数组中清除已参加排序的数据。[可优化成不挪动数据,只是用两个索引标记有效数据的起始和截止位置]
6.对400M内存中的有效数据[没装满]做快排。
将排好序的直接写文件。
7.再把每个数组尽量填充满。从第2步开始继续,知道各个文件都读区完毕。
这么做的好处有:
1.每个文件的内容只读区一次,且是批量读区。比每次只取一条快得多。
2.充分利用了读区到内存中的数据。曹源 同学在文件中查找那个中间数是会比较困难的。
3.每个拷贝到400M大数组中参加快排的数据都被写到了文件中,这样每个数只参加了一次快排。展开

sherry
2018-10-21
16
还是觉得伪代码更好,理解思路然后可以写成自己写练练手,看完代码后就没啥想写的欲望了。
作者回复: 真是众口难调啊😢

Lx
2018-10-23
15
合并函数借助哨兵简化方法
传入的后两个数组各在尾部多放一个和原有最后值相同的值。
循环改为:
while i<=q or j<=r do{
if A[i] <= A[j] and i<=q {
tmp[k++] = A[i++]
}
else{
tmp[k++] = A[j++]
}
}
可以在while循环里完成两个数组的清空,不需要专用部分完成。展开

冷笑的花猫
2018-10-17
13
老师您好,最后的思考题思路基本都是先拆成小文件,然后取出topK,最后再合并。疑惑的是内存不够,怎么读到内存中。如果不读到内存中该怎么实现,读不读到内存中的标准是什么?如果每个文件都是3g,内存只有1g,思路类似。老师能提供下详细的代码吗?相信绝大部分同学都有疑惑,谢谢。
展开

见贤思齐
2018-10-19
12
我测试出,伪代码中
'
partition(A, p, r) {
pivot := A[r]
i := p
for j := p to r-1 do {
if A[j] < pivot {
swap A[i] with A[j]
i := i+1
}
}
swap A[i] with A[r]
return i
'
' for j := p to r-1 do '
中的 r-1 应该是 r展开

yaya
2018-10-17
11
以前写快排的时候总是喜欢用第一个元素作为k值,partion喜欢用找到左右不符合规则的元素再对调,第k大总是纠结于,下次递归应该是第几大,😂这些其实只要把最后一个元素作为key就可以简化代码了。这门课让我懂了以前好多不懂得小细节。应该说曾经认为自己懂了吧,尤其是排序这里。
思考题,由于本来十个部分就是有序的,利用十个index,把这十个读入内存比较,在里面选择最小的一个index增1,如果一个部分放完了,就继续放剩下的九个部分,直到只剩一个部分,再复制。展开

The Sword...
2018-11-01
9
王道考研书上看到的快排算法,利用哨兵减少了交换两个元素的复杂步骤,效果更好一些
private static void quickSort(int[] a, int head, int tail) {
int low = head;
int high = tail;
int pivot = a[low];
if (low < high) {
while (low<high) {
while (low < high && pivot <= a[high]) high--;
a[low] = a[high];
while (low < high && pivot >= a[low]) low++;
a[high]=a[low];
}
a[low] = pivot;
if(low>head+1) quickSort(a,head,low-1);
if(high<tail-1) quickSort(a,high+1,tail);
}
}展开

oldman
2018-10-22
9
我用python实现了归并排序和快速排序,代码如下:
归并排序:https://github.com/lipeng1991/testdemo/blob/master/45_merge_sort.py
快速排序: https://github.com/lipeng1991/testdemo/blob/master/23_quick_sort.py
欢迎一起探讨。今天又回想了一下上一节的三个排序和今天的两个排序,自己又动手画了一下图,实现了一下代码,确切来讲,要想很深的掌握这些东西是需要不断的回想,不断的训练来加深印象的,想想以前学习算法为什么会感觉那么的难,其实就是练的不够,不要太着急的一下子把所有的算法都实现一遍,温故而知新,跟着老师的这个专栏来,一点一点的啃,啃着现在的复习前面的,你会越来越有成就感,你会越来越自信,这就是建立在不断的训练的基础上的。展开

朱月俊
2018-10-17
9
假设这十个文件都在本地,同时打开这十个文件,每个文件加一个offset,每次比较十个文件中每个文件最新的一条日志,按照时间戳获取时间戳最小的一条日志,然后对应文件offset加1,按照这种方法可以把在内存很小的情况下读完文件,积累一定大小记录在内存后flush到磁盘。
展开

姜威
2018-10-22
8
三、快速排序
1.算法原理
快排的思想是这样的:如果要排序数组中下标从p到r之间的一组数据,我们选择p到r之间的任意一个数据作为pivot(分区点)。然后遍历p到r之间的数据,将小于pivot的放到左边,将大于pivot的放到右边,将povit放到中间。经过这一步之后,数组p到r之间的数据就分成了3部分,前面p到q-1之间都是小于povit的,中间是povit,后面的q+1到r之间是大于povit的。根据分治、递归的处理思想,我们可以用递归排序下标从p到q-1之间的数据和下标从q+1到r之间的数据,直到区间缩小为1,就说明所有的数据都有序了。
递推公式:quick_sort(p…r) = quick_sort(p…q-1) + quick_sort(q+1, r)
终止条件:p >= r
2.代码实现(参见下一条留言)
3.性能分析
1)算法稳定性:
因为分区过程中涉及交换操作,如果数组中有两个8,其中一个是pivot,经过分区处理后,后面的8就有可能放到了另一个8的前面,先后顺序就颠倒了,所以快速排序是不稳定的排序算法。比如数组[1,2,3,9,8,11,8],取后面的8作为pivot,那么分区后就会将后面的8与9进行交换。
2)时间复杂度:最好、最坏、平均情况
快排也是用递归实现的,所以时间复杂度也可以用递推公式表示。
如果每次分区操作都能正好把数组分成大小接近相等的两个小区间,那快排的时间复杂度递推求解公式跟归并的相同。
T(1) = C; n=1 时,只需要常量级的执行时间,所以表示为 C。
T(n) = 2*T(n/2) + n; n>1
所以,快排的时间复杂度也是O(nlogn)。
如果数组中的元素原来已经有序了,比如1,3,5,6,8,若每次选择最后一个元素作为pivot,那每次分区得到的两个区间都是不均等的,需要进行大约n次的分区,才能完成整个快排过程,而每次分区我们平均要扫描大约n/2个元素,这种情况下,快排的时间复杂度就是O(n^2)。
前面两种情况,一个是分区及其均衡,一个是分区极不均衡,它们分别对应了快排的最好情况时间复杂度和最坏情况时间复杂度。那快排的平均时间复杂度是多少呢?T(n)大部分情况下是O(nlogn),只有在极端情况下才是退化到O(n^2),而且我们也有很多方法将这个概率降低。
3)空间复杂度:快排是一种原地排序算法,空间复杂度是O(1)
四、归并排序与快速排序的区别
归并和快排用的都是分治思想,递推公式和递归代码也非常相似,那它们的区别在哪里呢?
1.归并排序,是先递归调用,再进行合并,合并的时候进行数据的交换。所以它是自下而上的排序方式。何为自下而上?就是先解决子问题,再解决父问题。
2.快速排序,是先分区,在递归调用,分区的时候进行数据的交换。所以它是自上而下的排序方式。何为自上而下?就是先解决父问题,再解决子问题。
五、思考
1.O(n)时间复杂度内求无序数组中第K大元素,比如4,2,5,12,3这样一组数据,第3大元素是4。
我们选择数组区间A[0...n-1]的最后一个元素作为pivot,对数组A[0...n-1]进行原地分区,这样数组就分成了3部分,A[0...p-1]、A[p]、A[p+1...n-1]。
如果如果p+1=K,那A[p]就是要求解的元素;如果K>p+1,说明第K大元素出现在A[p+1...n-1]区间,我们按照上面的思路递归地在A[p+1...n-1]这个区间查找。同理,如果K<p+1,那我们就在A[0...p-1]区间查找。
时间复杂度分析?
第一次分区查找,我们需要对大小为n的数组进行分区操作,需要遍历n个元素。第二次分区查找,我们需要对大小为n/2的数组执行分区操作,需要遍历n/2个元素。依次类推,分区遍历元素的个数分别为n、n/2、n/4、n/8、n/16......直到区间缩小为1。如果把每次分区遍历的元素个数累加起来,就是等比数列求和,结果为2n-1。所以,上述解决问题的思路为O(n)。
2.有10个访问日志文件,每个日志文件大小约为300MB,每个文件里的日志都是按照时间戳从小到大排序的。现在需要将这10个较小的日志文件合并为1个日志文件,合并之后的日志仍然按照时间戳从小到大排列。如果处理上述任务的机器内存只有1GB,你有什么好的解决思路能快速地将这10个日志文件合并?展开








![蓝桥杯刷题 深度优先搜索-[NewOJ P1158]N皇后(C++)](https://img-blog.csdnimg.cn/img_convert/f23b0934bc3f31c4a5b3a5966f41919d.png)

