目录

1，熟悉简单的矩阵输入

1.1，创建矩阵

1.2，在命令行调用文件中的变量

1.3，ones函数

1.4，who和whos的使用

2，绘制信号曲线 

2.1，实指数信号 

2.2，频率为50Hz的周期方波信号

2.3，信号卷积 *

2.4，产生从-4π到4π的Sa(t)函数

2.5，阶跃信号u(t)

2.6，g(t)=u(t)-u(t-1)

2.7，冲激信号δ(t)

1）stem函数

2.8，u(n-3)

2.9  冲击序列δ(n)

---

1，熟悉简单的矩阵输入

1.1，创建矩阵

在命令窗口输入矩阵A=[123;456;789]或A=[1,2,3;4,5,6;7,8,9]观察输出结果。

  

观察结果，可知：

经观察可以发现，在创建矩阵的时候如果不在每列数字中间加上逗号或者是空格，那么每一列都会很紧凑的挨在一起。如果不想要使用逗号的话，可以直接使用空格键，让每列分开。

用回车代替矩阵里面的分号，观察输出结果。

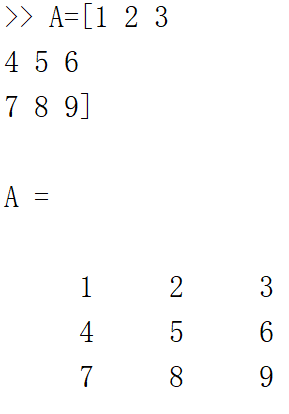
观察结果，可知：

输出依旧能够实现矩阵的样式，且更加方便，不用写分号。唯一不足就是定义矩阵的时候占用的行过多，不利于观察。我还是比较喜欢使用分号来分开每一行。

1.2，在命令行调用文件中的变量

选择Filenew菜单中的M-file，输入B=[9,8,7;6,5,4;3,2,1]

保存为B1.m文件，退出编辑环境。此时在命令窗口中使用B1命令就

可调出B矩阵。

需要注意的是，变量名和脚本名不能同名，不然就会无法识别。

如果B1.m文件不在project工程目录下，就会有如下结果：

这个时候可以直接使用window自带的拖拽功能，直接将文件拖拽到project目录下即可。

1.3，ones函数

输入x=ones(3,4),观察输出结果。

观察结果：

Ones有1的意思，在创建矩阵时，会用1来填充矩阵的所有行和列。

1.4，who和whos的使用

输入who和whos观察结果，了解其作用。

 观察结果并了解到其作用：

who只是简单的列出了同一个工程下所有文件的变量名。

whos相比于who列出的信息更详细，如：该变量的名字，大小，类型和所占的字节。

2，绘制信号曲线 

2.1，实指数信号 

%f(t)=3e-t;
%(t>0(取适当的△t)
dt=0.01;
t=0:dt:5;
y=3*exp(-t);
plot(t,y);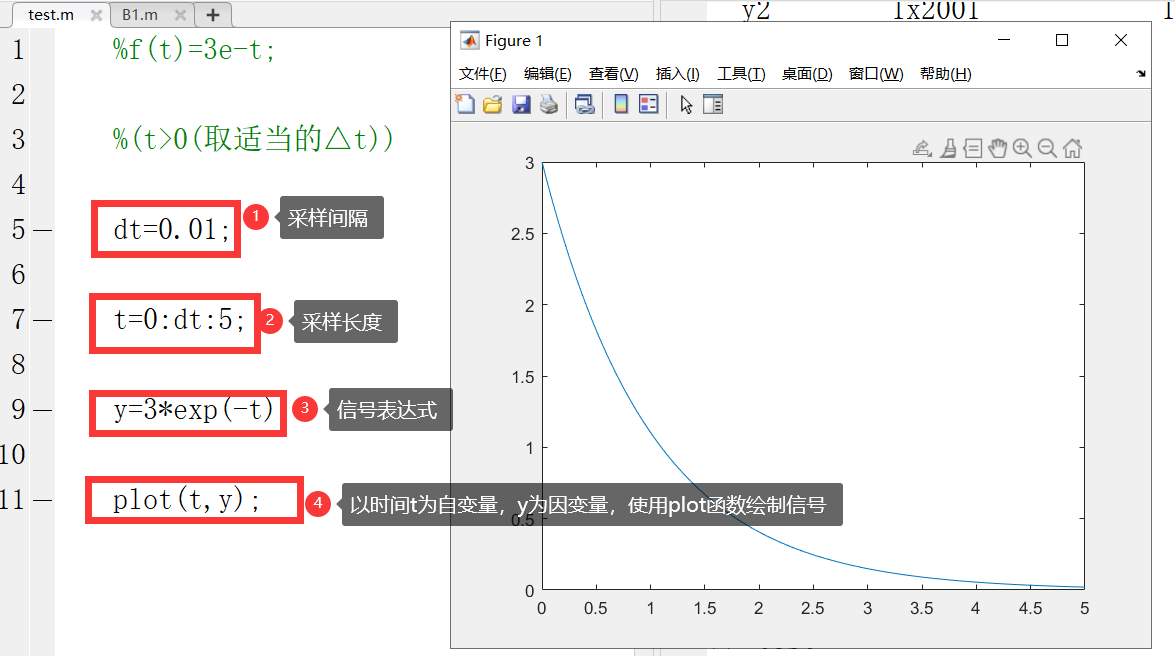

 产生3-e^(-t)的信号

%f(t)=3-e-t;
%(t>0(取适当的△t)
dt=0.01;
t=0:dt:5;
y=3-exp(-t);   % exp表示以常数e为底的指数函数
plot(t,y);

2.2，频率为50Hz的周期方波信号

dt=0.001;    % 采样间隔为0.001s
t=0:dt:1;
y=square(2*pi*50*t);
plot(t,y);
axis([0,0.1,-1.1,1.1]);
title('·½²方波');
xlabel('时间/s');
ylabel('幅度/db');
axis manual;

axis - 设置坐标轴范围和纵横比。此 MATLAB 函数 指定当前坐标区的范围。以包含 4 个、6 个或 8 个元素的向量形式指定范围。

2.3，信号卷积 *

%f(t)=e^(-t)  % 实指数信号
%sin(2лt)(0<t<3)
dt=0.01;
t=0:dt:5;
y=exp(-t).*sin(2*pi*t);  % exp表示以常数e为底的指数函数
plot(t,y);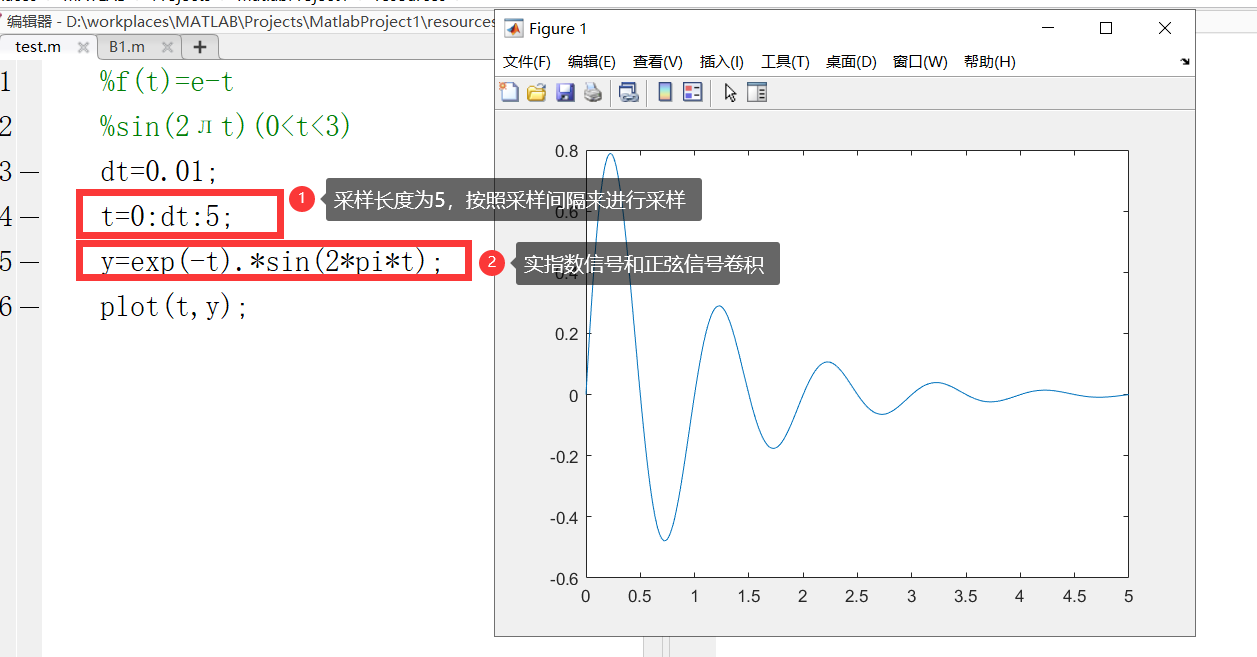

2.4，产生从-4π到4π的Sa(t)函数

%f(t)=sa(t); 样本函数
%(t>0(取适当的△t)
dt=0.001;
t=-4*pi:dt:4*pi;
y=sin(t)./t;
plot(t,y);

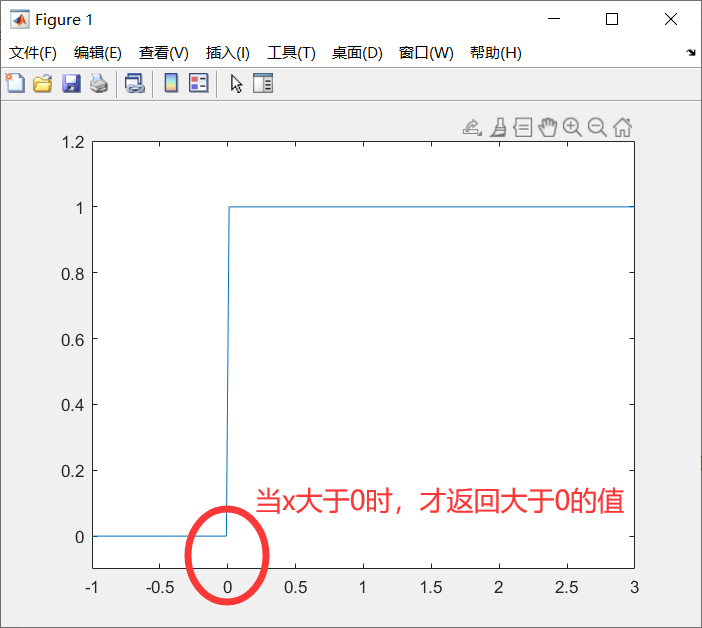
2.5，阶跃信号u(t)

t=-1:0.01:3;
f=heaviside(t);
plot(t,f);
axis([-1 3 -0.1 1.2]);

在Matlab中，heaviside函数用于计算阶跃函数。这个函数以0为分界点，当函数的自变量小于0时返回0，当自变量等于0时返回0.5，当自变量大于0时返回1。例如，heaviside(2)返回1,heaviside(-3)返回0， heaviside(0)返回0.5。 

2.6，g(t)=u(t)-u(t-1)

依旧可以使用heaviside函数来生成u(t-1)，如下👇 

t=0:0.01:3;
f1=heaviside(t);  % u(t)
f2=heaviside(t-1);% u(t-1)
g=f1-f2;          % u(t)-u(t-1)
plot(t,g);
axis([0 3 -2 2]);

 如果想要绘制u(t-2)的信号，可以用heaviside（t-2）。

2.7，冲激信号δ(t)

t = (-1:0.0001:1);  % 中间的0.0001是采样间隔，也可以理解为采样周期，采样周期越小，采样频率就会越大，得到的图像就越是我们想要的结果
impulse = t==0;     % 冲击信号只有在t=0时才有取值，其它部分值为0
plot(t,impulse);

1）stem函数

stem函数主要用于绘制离散序列，而plot用于绘制连续信号。如下，我先用stem函数来绘制离散的正弦信号，👇 

x=0:0.1:2*pi;
y=sin(x);
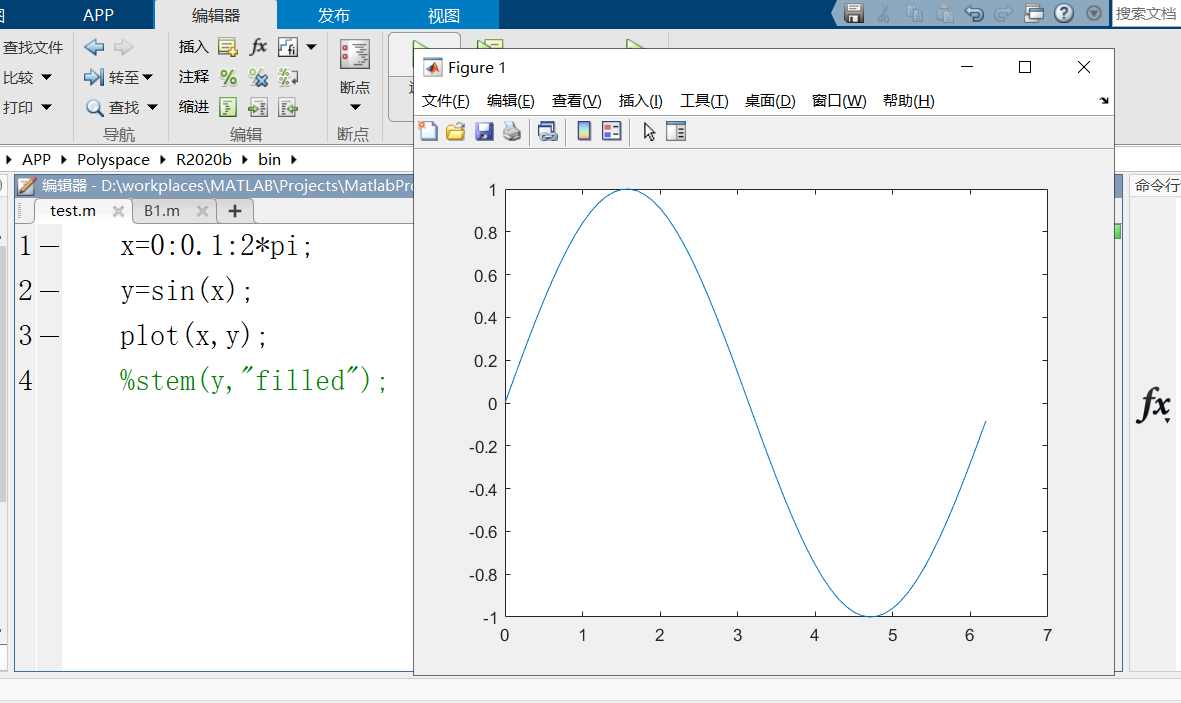
stem(y,"filled");

 对应的效果如下图：

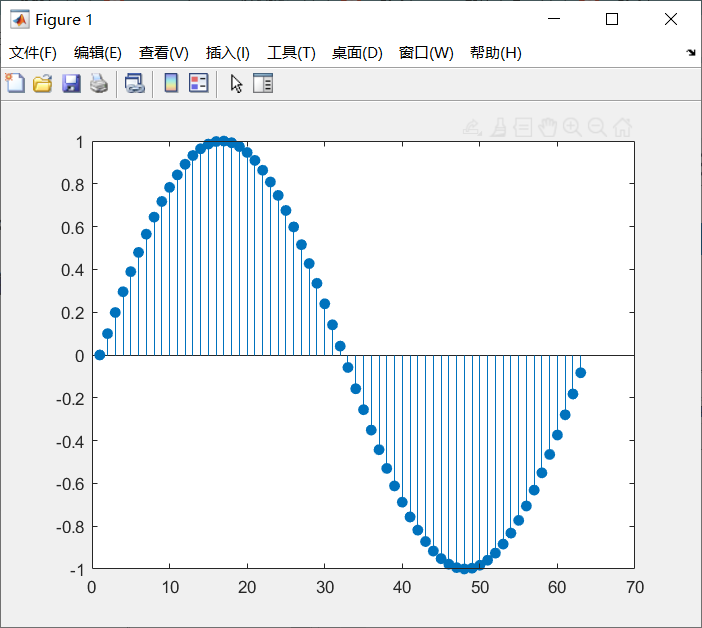
 如果我用plot函数来代替stem函数，得到的就是下图：

2.8，u(n-3)

绘制u(x-3)延迟阶跃信号有两种方法，一种是使用heaviside函数，另外一种就是使用表达式，如下，都可以得到图中的信号图👇

t=0:0.001:6;
y=heaviside(t-3);  % 使用heaviside函数绘制阶跃信号
%y=(t>3);  % 阶跃信号只有在指定初始位置之后才有值，之前的值为0
plot(t,y);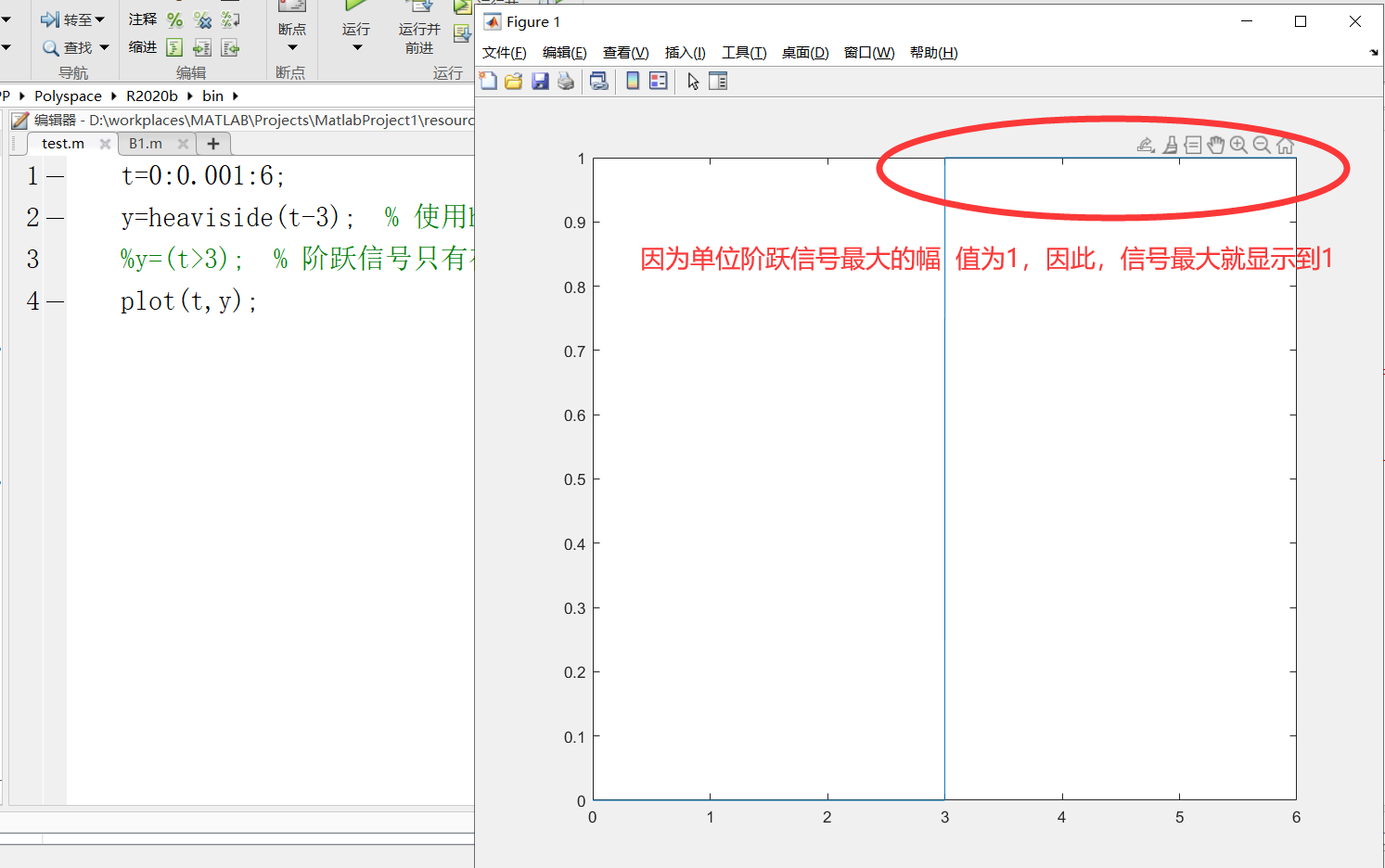

如果觉得y轴太“矮”，想要自定义高度，也可以，我就需要使用到之前的axis坐标轴函数来设置x和y相应的坐标，如下👇

t=0:0.01:6;
%y=heaviside(t-3);  % 使用heaviside函数绘制阶跃信号
y=(t>=3);  % 阶跃信号只有在指定初始位置之后才有值，之前的值为0
plot(t,y);
axis([-1 6 0 2]);

如果想要离散的时间序列，可以将plot函数替换成stem函数，如下👇

n=0:0.001:6;
y=heaviside(n-3);  % 使用heaviside函数绘制阶跃信号
%y=(n>3);  % 阶跃信号只有在指定初始位置之后才有值，之前的值为0
%plot(n,y);
stem(n,y);  % 绘制离散序列

因为在对连续时间信号进行抽样时，我使用的是按照采样周期0.001来进行采样，所以，就会显示出有无数多个单位冲击序列组成的单位阶跃序列，如果放大蓝色区域就可以看到冲击序列，如下图👇

如果不想要那么密集的显示，可以将采样周期删除掉，如下图👇

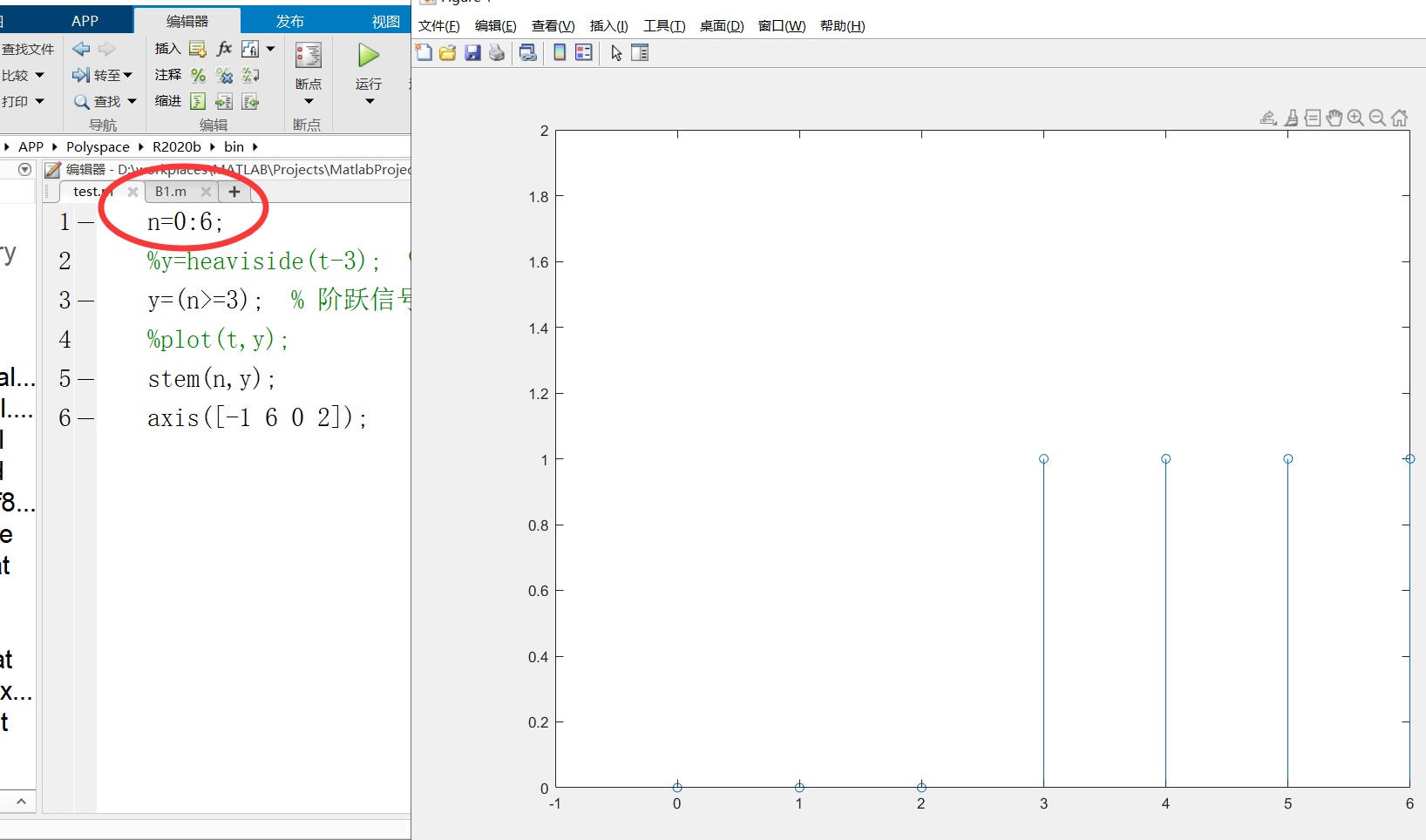
2.9  冲击序列δ(n)

n=-1:3;
y=(n==0);
stem(n,y);

有问题请在评论区留言或者是私信我，一天8h在线。