一文搞懂从爬楼梯到最小花费（力扣70,746）

news2024/11/27 3:43:23

文章目录

题目
前知
- 动态规划简介
- 动态规划模版
爬楼梯
- 一、思路
- 二、解题方法
- 三、Code
使用最小花费爬楼梯
- 一、思路
- 二、解题方法
- 三、Code
总结

在计算机科学中，动态规划是一种强大的算法范例，用于解决多种优化问题。本文将介绍动态规划的核心思想，并通过两个经典的力扣题目展示其应用：爬楼梯（LeetCode 70）和使用最小花费爬楼梯（LeetCode 746）

题目

Problem: 70. 爬楼梯
Problem: 746. 使用最小花费爬楼梯

爬楼梯
假设你正在爬楼梯。需要 n 阶你才能到达楼顶。每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢？

示例 1：

输入：n = 2
输出：2
解释：有两种方法可以爬到楼顶。

1 阶 + 1 阶
2 阶

示例 2：

输入：n = 3
输出：3
解释：有三种方法可以爬到楼顶。

1 阶 + 1 阶 + 1 阶
1 阶 + 2 阶
2 阶 + 1 阶

使用最小花费爬楼梯
给你一个整数数组 cost ，其中 cost[i] 是从楼梯第 i个台阶向上爬需要支付的费用。一旦你支付此费用，即可选择向上爬一个或者两个台阶。
你可以选择从下标为 0 或下标为 1 的台阶开始爬楼梯。请你计算并返回达到楼梯顶部的最低花费。

示例 1：

输入：cost = [10,15,20]
输出：15
解释：你将从下标为 1 的台阶开始。

支付 15 ，向上爬两个台阶，到达楼梯顶部。
总花费为 15 。

示例 2：

输入：cost = [1,100,1,1,1,100,1,1,100,1]
输出：6
解释：你将从下标为 0 的台阶开始。

支付 1 ，向上爬两个台阶，到达下标为 2 的台阶。
支付 1 ，向上爬两个台阶，到达下标为 4 的台阶。
支付 1 ，向上爬两个台阶，到达下标为 6 的台阶。
支付 1 ，向上爬一个台阶，到达下标为 7 的台阶。
支付 1 ，向上爬两个台阶，到达下标为 9 的台阶。
支付 1 ，向上爬一个台阶，到达楼梯顶部。
总花费为 6 。

前知

动态规划简介

动态规划算法（Dynamic Programming）是一种解决多阶段决策过程最优化问题的方法。它将问题分解为相互重叠的子问题，并通过解决子问题来解决整个问题。这种方法通常用于具有重叠子问题和最优子结构性质的问题。

动态规划的基本思想是将原问题分解为相互重叠的子问题，并在解决这些子问题时进行存储，以避免重复计算。通过这种方式，可以大大减少计算量，提高算法效率。动态规划算法通常涉及两个关键步骤：定义状态和状态转移方程。

定义状态：确定问题中的状态变量，并定义状态之间的关系。状态变量描述问题的当前情况，是动态规划算法的关键。
状态转移方程：建立状态之间的转移关系，描述如何从一个状态转移到另一个状态。这个方程描述了问题的最优子结构，是动态规划算法的核心。

动态规划算法通常用于解决一些优化问题，例如最长公共子序列、最短路径、背包问题等。在实际应用中，动态规划常常能够以较高效率解决一些复杂的问题，但需要注意的是，有时需要权衡时间和空间复杂度。

与贪心算法的区别：

最优子结构性质：

动态规划：动态规划问题具有最优子结构性质，即问题的最优解可以通过子问题的最优解来构造。在解决动态规划问题时，通常需要考虑所有可能的子问题，并选择其中最优的解进行组合。
贪心算法：贪心算法也寻求问题的最优解，但它通常通过在每个步骤中选择当前状态下的局部最优解来构造全局最优解。贪心算法没有最优子结构性质，它只关注当前状态下的最优选择，而不考虑后续状态的影响。

状态的存储与重复计算：

动态规划：动态规划算法通常利用存储来避免重复计算子问题，因此可以在解决问题时节省计算时间。通过记忆化搜索或者建立动态规划表格，可以将子问题的解存储起来，以便后续使用。
贪心算法：贪心算法通常不需要存储中间状态或者解决方案，因为它只关注当前状态下的最优选择。这意味着贪心算法通常需要更少的存储空间。

适用范围：

动态规划：动态规划通常适用于具有重叠子问题和最优子结构性质的问题，例如最长公共子序列、最短路径、背包问题等。这些问题通常需要考虑多阶段决策过程，而动态规划能够有效地处理这种情况。
贪心算法：贪心算法通常适用于具有贪心选择性质的问题，即每个步骤都可以做出局部最优选择，并且这些局部最优选择能够导致全局最优解。贪心算法通常更简单、更高效，但只适用于部分问题，因为它没有考虑全局的影响。

动态规划模版

与之前讲的递归三部曲还有回溯三部曲都是类似的

动规五部曲：在这里面dp数组是非常重要的，一定要搞清楚dp数组的含义究竟是什么含义

在这里插入图片描述

确定dp数组（dp table）以及下标的含义
确定递推公式
dp数组如何初始化
确定遍历顺序
举例推导dp数组

爬楼梯

一、思路

第二层可以由第一层爬一个楼梯上来或者由第零层爬两个楼梯上来，二层以上都可以这样推出来，于是只要求出第零层和第一层的上楼方法就可以了

二、解题方法

动规五部曲

确定dp数组及下标i的含义：到达i层有dp[i]种不同的方法
确定递推公式：dp[i] = dp[i-1] + dp[i-2]，第2层由第零层dp[0]或第一层dp[1]下一步得出，在推导dp[i]的时候，一定要时刻想着dp[i]的定义，否则容易跑偏。这体现出确定dp数组以及下标的含义的重要性！
dp数组如何初始化：两层之后都可以由dp[0]和dp[1]得出
确定遍历顺序：从递推公式dp[i] = dp[i - 1] + dp[i - 2];中可以看出，遍历顺序一定是从前向后遍历的
举例推导dp数组：当n=5时dp数组应该是这样的：

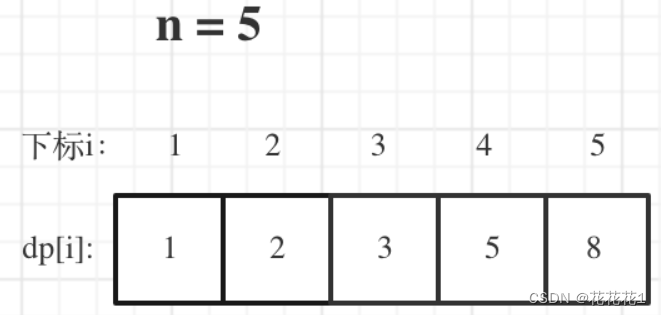
在这里插入图片描述

三、Code

class Solution {
    public int climbStairs(int n) {
        int[] dp =new int[n+1];
        dp[0] = 1;
        dp[1] = 1;
        for(int i=2;i<=n;i++){
            dp[i] = dp[i-1] + dp[i-2];
        }
        return dp[n];
    }
}

使用最小花费爬楼梯

一、思路

此题在上一题的基础上进行了爬楼梯需要耗费cost数组所需的体力，才能够向上爬，而站在起点0或起点1是不需要耗费体力的

二、解题方法

动规五部曲

确定dp数组及下标i的含义：到达第i个台阶所需要的最小花费为dp[i]
确定递推公式：因为可以一次跳一个或两个台阶，所以dp[i]有两种方式得到，由dp[i-1]加上离开这层所需花费的cost[i-1]或者由dp[i-2]加上离开这层所需花费的cost[i-2]，从两种情况中选最小的那个，所以要用Math.min(...,...)对两个结果进行比较得到dp[i]
dp数组如何初始化：只需要初始化dp[0]和dp[1]即可，其它dp都可以由这两个推出来，题目说可以选择从下标为 0 或下标为 1 的台阶开始爬楼梯，所以dp[0]和dp[1]都为0，不需要花费
确定遍历顺序：从前到后遍历cost数组
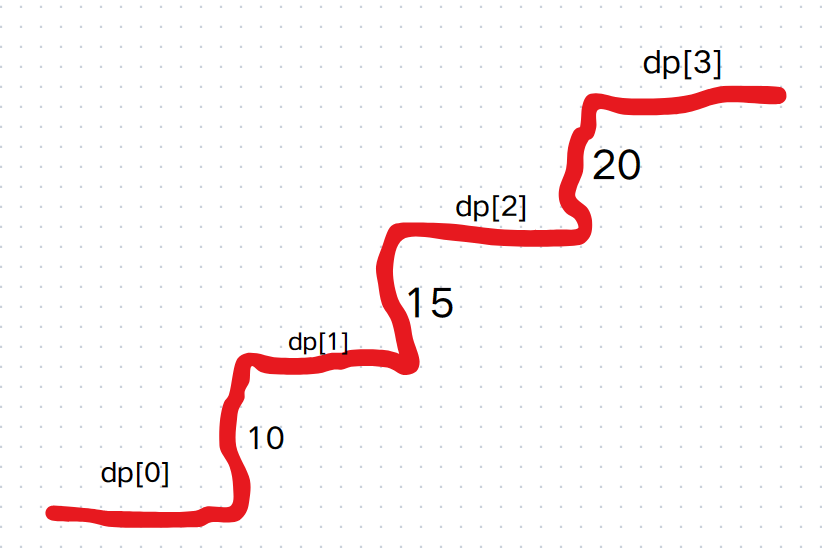
举例推导dp数组：用题目给的实例1进行举例，cost = [10,15,20]，可以推出dp[0]=0，dp[1]=0，dp[2]=dp[0]+cost[0]=10，dp[3]=dp[1]+cost[1]=15。最后输出的确实是dp[3]=15。如下图所示：

三、Code

class Solution {
    public int minCostClimbingStairs(int[] cost) {
        // 到达第i层的最小花费dp[i]
        int[] dp = new int[cost.length + 1];

        dp[0] = 0;
        dp[1] = 0;
        // 最上面还有一层，台阶cost数组有三个，但是有四层楼梯
        for (int i = 2; i <= cost.length; i++) {
            dp[i] = Math.min(dp[i - 1] + cost[i - 1], dp[i - 2] + cost[i - 2]);
        }
        return dp[cost.length];
    }
}