Deformable Convolutional Networks论文阅读
- Abstract
- 1. Introduction
- 2. Deformable Convolutional Networks
- 2.1. Deformable Convolution
- 2.2. Deformable RoI Pooling
- 总结
文章信息:

原文链接:https://arxiv.org/abs/1703.06211
源代码:https://github.com/msracver/Deformable-ConvNets
Abstract
这项工作介绍了两个新模块,以增强卷积神经网络(CNNs)的变换建模能力,分别是可变形卷积(deformable convolution)和可变形RoI池化(deformable RoI pooling)。这两个模块的基本思想是在模块中增加额外的偏移量,从而增强空间采样位置的变换能力,并从目标任务中学习这些偏移量,无需额外的监督。这些新模块可以直接替换现有CNNs中的普通模块,并且可以通过标准的反向传播方法轻松进行端到端的训练,从而产生可变形卷积网络(deformable convolutional networks)。大量实验证实了我们方法的性能。我们首次展示,在深度CNNs中学习密集空间变换对于复杂的视觉任务,如目标检测和语义分割,是有效的。该代码已发布在https://github.com/msracver/Deformable-ConvNets。
1. Introduction
视觉识别中的一个关键挑战是如何适应对象尺度、姿态、视点和部分变形的几何变化,或者模拟几何变换。一般来说,有两种方法。第一种方法是构建具有足够所需变化的训练数据集。这通常通过对现有数据样本进行增广来实现,例如通过仿射变换。可以从数据中学习到稳健的表示,但通常以昂贵的训练成本和复杂的模型参数为代价。第二种方法是使用具有变换不变性的特征和算法。这一类别涵盖了许多众所周知的技术,例如SIFT(尺度不变特征变换)[42]和基于滑动窗口的对象检测范式。
上述方法存在两个缺点。首先,假设几何变换是固定且已知的。这种先验知识被用来增广数据,并设计特征和算法。这种假设阻止了对具有未知几何变换的新任务的泛化,因为这些未知变换没有得到合适的建模。其次,手工设计不变特征和算法可能会对过于复杂的变换变得困难或不可行,即使这些变换是已知的。
最近,卷积神经网络(CNNs)[35] 在视觉识别任务中取得了显著的成功,例如图像分类[31]、语义分割[41]和目标检测[16]。然而,它们仍然具有上述两个缺点。它们对于建模几何变换的能力主要来自于大量的数据增强、大模型容量以及一些简单的手工设计模块(例如,用于小平移不变性的最大池化[1])。
简而言之,卷积神经网络(CNNs)固有地受限于对大型、未知变换的建模能力。这种限制源于CNN模块的固定几何结构:卷积单元在固定位置对输入特征图进行采样;池化层以固定比例减少空间分辨率;RoI(感兴趣区域)池化层将感兴趣区域分割成固定的空间区域,等等。缺乏内部机制来处理几何变换。这导致了明显的问题。举一个例子,同一CNN层中所有激活单元的感受野大小都相同。这对于编码空间位置上的语义的高级CNN层来说是不可取的。因为不同位置可能对应着具有不同尺度或变形的对象,因此在需要进行精细定位的视觉识别中,例如使用全卷积网络进行语义分割[41],适应性地确定尺度或感受野大小是可取的。举另一个例子,尽管目标检测最近取得了显著而迅速的进展[16, 52, 15, 47, 46, 40, 7],但所有方法仍然依赖于基于原始边界框的特征提取。这显然是次优的,尤其是对于非刚性对象。
在这项工作中,我们引入了两个新模块,大大增强了CNNs对建模几何变换的能力。
第一个是可变形卷积。它在标准卷积中的常规网格采样位置上添加了2D偏移量。这样可以自由地对采样网格进行形变。如图1所示。这些偏移量是通过额外的卷积层从前面的特征图中学习到的。因此,变形是根据输入特征以局部、密集和自适应的方式进行条件化的。
第二个模块是可变形RoI池化。它在前一个RoI池化[15, 7]的常规bin分区中为每个bin位置添加了一个偏移量。类似地,这些偏移量是通过前面的特征图和RoIs学习到的,从而实现了对具有不同形状的对象进行自适应的部分定位。
这两个模块都是轻量级的。它们只添加了少量的参数和计算用于偏移量的学习。它们可以轻松地替换深度CNNs中的普通模块,并且可以通过标准的反向传播方法进行端到端的训练。由此产生的CNNs被称为可变形卷积网络,或称为可变形ConvNets。
我们的方法与空间变换网络[26]和可变形部件模型[11]在高层次上有类似的精神。它们都具有内部的变换参数,并且纯粹从数据中学习这些参数。可变形ConvNets的一个关键区别在于,它们以简单、高效、深度和端到端的方式处理密集空间变换。在第3.1节中,我们详细讨论了我们的工作与之前工作的关系,并分析了可变形ConvNets的优越性。
2. Deformable Convolutional Networks
CNNs中的特征图和卷积是3D的。可变形卷积和RoI池化模块都在2D空间域上操作。在通道维度上,操作保持不变。为了符号清晰,这里对模块进行了2D描述,但可以轻松地扩展到3D。
2.1. Deformable Convolution
2D卷积由两个步骤组成:
1)使用规则网格
R
\mathcal{R}
R在输入特征图
x
x
x上进行采样;
2)对采样值按权重
w
w
w进行求和。网格
R
\mathcal{R}
R定义了感受野大小和膨胀率。例如,

定义了一个具有膨胀率为1的3 × 3内核。
对于输出特征图
y
y
y上的每个位置
p
0
p_0
p0,我们有
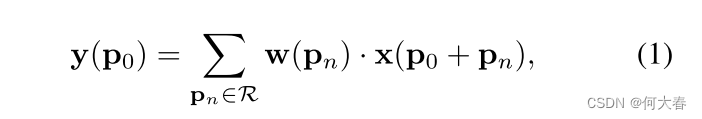
其中
p
n
p_n
pn枚举
R
\mathcal{R}
R中的位置。
在可变形卷积中,常规网格 R \mathcal{R} R被增加了偏移量 { Δ p n ∣ n = 1 , . . . , N } \{\Delta\mathbf{p}_n|n=1,...,N\} {Δpn∣n=1,...,N},其中 N = ∣ R ∣ N=|\mathcal{R}| N=∣R∣。方程(1)变为
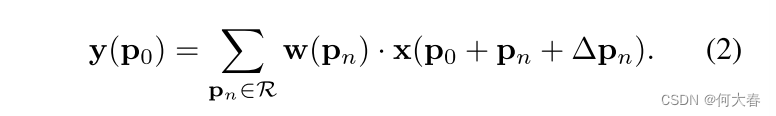
现在,采样是在不规则和偏移位置
p
n
+
Δ
p
n
\mathbf{p}_n+\Delta\mathbf{p}_n
pn+Δpn上进行的。由于偏移
Δ
p
n
\Delta\mathbf{p}_n
Δpn通常是分数,因此方程(2)是通过双线性插值来实现的,如下所示:
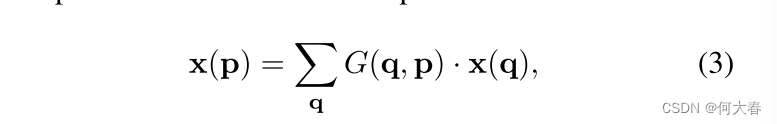
其中,p表示任意(分数)位置(对于方程(2),p =
p
0
+
p
n
+
Δ
p
n
\mathbf{p}_0+\mathbf{p}_n+\Delta\mathbf{p}_n
p0+pn+Δpn),q枚举特征图x中的所有整数空间位置,而
G
(
⋅
,
⋅
)
G(\cdot,\cdot)
G(⋅,⋅)是双线性插值核函数。请注意,
G
G
G是二维的。它被分解为两个一维核函数,如下所示:
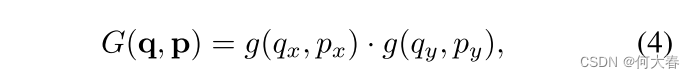
其中
g
(
a
,
b
)
=
max
(
0
,
1
−
∣
a
−
b
∣
)
。
方程
(
3
)
的计算速度
较快,因为只有少数
q
s
的
G
(
q
,
p
)
非零。
\begin{aligned}&\mathrm{其中~}g(a,b) = \max(0,1 - |a - b|)。 \mathrm{方程~(3)~的计算速度}\\&\mathrm{较快,因为只有少数\mathbf{qs}的}G(\mathbf{q},\mathbf{p})\mathrm{非零。}\end{aligned}
其中 g(a,b)=max(0,1−∣a−b∣)。方程 (3) 的计算速度较快,因为只有少数qs的G(q,p)非零。
如图2所示,偏移量是通过对同一输入特征图应用卷积层获得的。卷积核的空间分辨率和膨胀率与当前卷积层相同(例如,图2中也是3×3膨胀率为1的卷积核)。输出偏移场具有与输入特征图相同的空间分辨率。通道维度2N对应于N个二维偏移量。在训练期间,用于生成输出特征和偏移量的卷积核都同时进行学习。为了学习偏移量,梯度通过方程(3)和方程(4)中的双线性操作进行反向传播。详情请参见附录A。
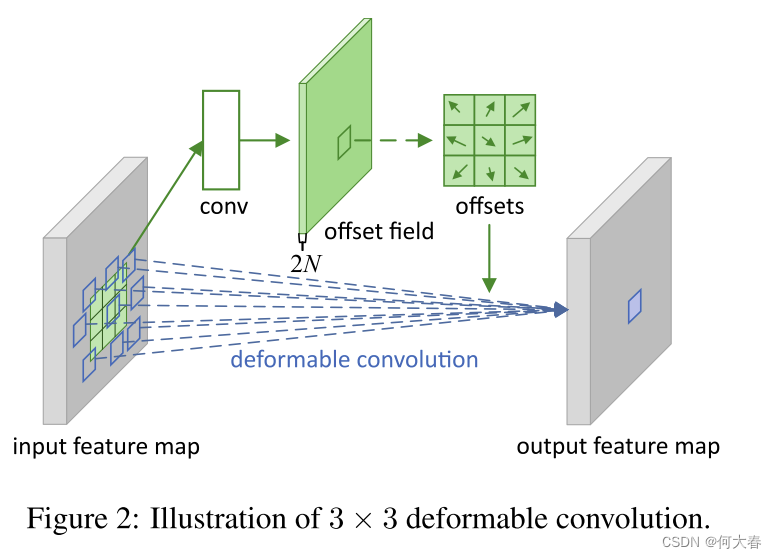
2.2. Deformable RoI Pooling
RoI池化在所有基于区域提议的目标检测方法中都被使用[16, 15, 47, 7]。它将任意大小的输入矩形区域转换为固定大小的特征。
RoI池化[15]:给定输入特征图
x
x
x和大小为
w
×
h
w\times h
w×h且左上角为
p
0
p_0
p0的RoI,RoI池化将RoI划分为
k
×
k
k\times k
k×k(
k
k
k是一个自由参数)个bin,并输出一个
k
×
k
k\times k
k×k的特征图
y
y
y。对于第
(
i
,
j
)
(i, j)
(i,j)个bin(
0
≤
i
,
j
<
k
0 \leq i, j < k
0≤i,j<k),我们有
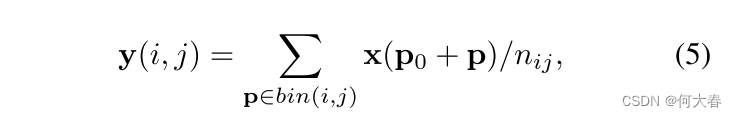
其中
n
i
j
是该bin中像素的数量。第
(
i
,
j
)
-个
bin跨越的范围为
⌊
i
w
k
⌋
≤
p
x
<
⌈
(
i
+
1
)
w
k
⌉
和
⌊
j
h
k
⌋
≤
p
y
<
⌈
(
j
+
1
)
h
k
⌉
。
\begin{aligned}&\text{其中 }n_{ij}\text{ 是该bin中像素的数量。第}(i,j)\text{-个}\\&\text{bin跨越的范围为 }\lfloor i\frac wk\rfloor \leq p_x < \lceil(i + 1)\frac wk\rceil\text{ 和 }\lfloor j\frac hk\rfloor \leq p_y <\\&\lceil(j+1)\frac hk\rceil。\end{aligned}
其中 nij 是该bin中像素的数量。第(i,j)-个bin跨越的范围为 ⌊ikw⌋≤px<⌈(i+1)kw⌉ 和 ⌊jkh⌋≤py<⌈(j+1)kh⌉。
类似于方程(2),在可变形RoI池化中,将偏移量
{
Δ
p
i
j
∣
0
≤
i
,
j
<
k
}
\{\Delta\mathbf{p}_{ij}|0\leq i,j<k\}
{Δpij∣0≤i,j<k}添加到空间分bin的位置上。方程(5)变为:
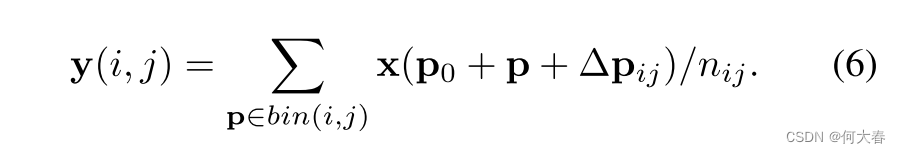
通常, Δ p i j \Delta\mathbf{p}_{ij} Δpij是分数。方程(6)通过方程(3)和(4)通过双线性插值来实现。
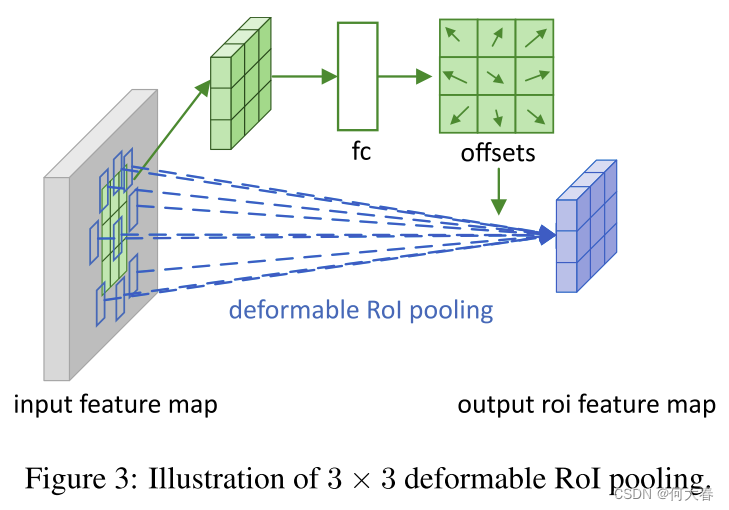
图 3 \color{red}{3} 3说明了如何获取偏移量。首先,RoI池化(方程(5))生成池化的特征图。从这些特征图中,一个全连接层生成了归一化的偏移量 Δ p ^ i j \Delta\widehat{\mathbf{p}}_{ij} Δp ij,然后通过逐元素乘积与RoI的宽度和高度,将其转换为方程(6)中的偏移量 Δ p i j \Delta\mathbf{p}_{ij} Δpij,即 Δ p i j = γ ⋅ Δ p ^ i j ∘ ( w , h ) \Delta\mathbf{p}_{ij}=\gamma\cdot\Delta\widehat{\mathbf{p}}_{ij}\circ(w,h) Δpij=γ⋅Δp ij∘(w,h)。这里 γ \gamma γ是一个预定义的标量,用于调节偏移量的大小。经验上设定 γ = 0.1 \gamma=0.1 γ=0.1。偏移量的归一化是必要的,以使偏移量学习对RoI大小不变。全连接层通过反向传播进行学习,详细内容请参见附录A。
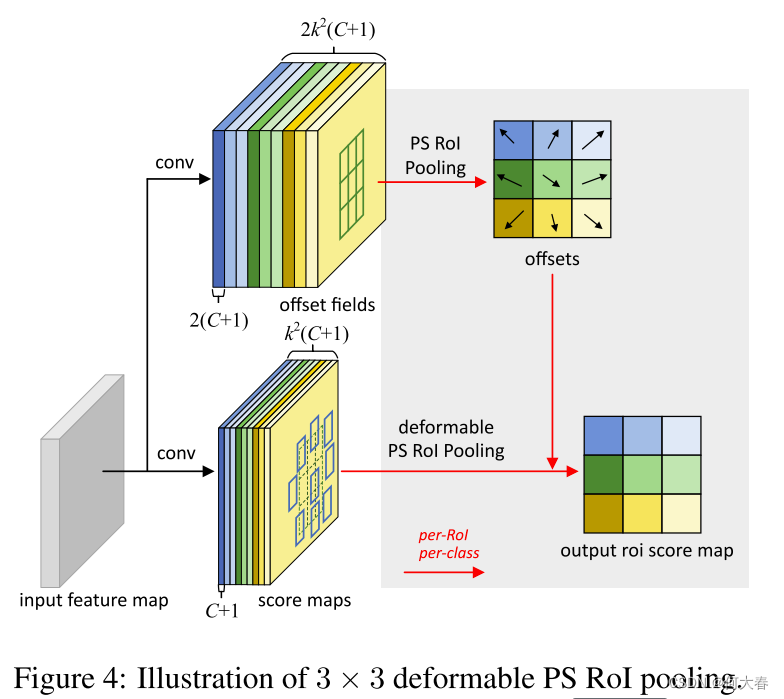
位置敏感(PS)RoI池化[7]是完全卷积的,与RoI池化不同。通过一个卷积层,所有输入特征图首先被转换为每个对象类别(总共 C + 1 C+1 C+1个,其中 C C C个是对象类别)的 k 2 k^2 k2个得分图,如图 4 \color{red}{4} 4底部分支所示。不需要区分类别,这些得分图被表示为 { x i , j } \{\mathbf{x}_{i,j}\} {xi,j},其中 ( i , j ) (i,j) (i,j)枚举所有的bin。在这些得分图上进行池化。 ( i , j ) (i,j) (i,j)-th bin的输出值通过从对应于该bin的一个得分图 x i , j \mathbf{x}_{i,j} xi,j中进行求和而获得。简而言之,与方程(5)中的RoI池化的不同之处在于,通用特征图 x x x被替换为特定的位置敏感得分图 x i , j \mathbf{x}_{i,j} xi,j。
在可变形PS RoI池化中,方程(6)中唯一的改变是 x x x也被修改为 x i , j \mathrm{x}_{i,j} xi,j。然而,偏移量的学习是不同的。它遵循[7]中的“完全卷积”精神,如图 4 \color{red}{4} 4所示。在顶部分支中,一个卷积层生成全空间分辨率的偏移场。对于每个RoI(也是每个类别),PS RoI池化被应用在这些字段上以获得 n o r m a l i z e d normalized normalized偏移量 Δ p ^ i j \Delta\widehat{\mathbf{p}}_{ij} Δp ij,然后将它们以与上述描述的可变形RoI池化相同的方式转换为真实的偏移量 Δ p i j \Delta\mathbf{p}_{ij} Δpij。
总结
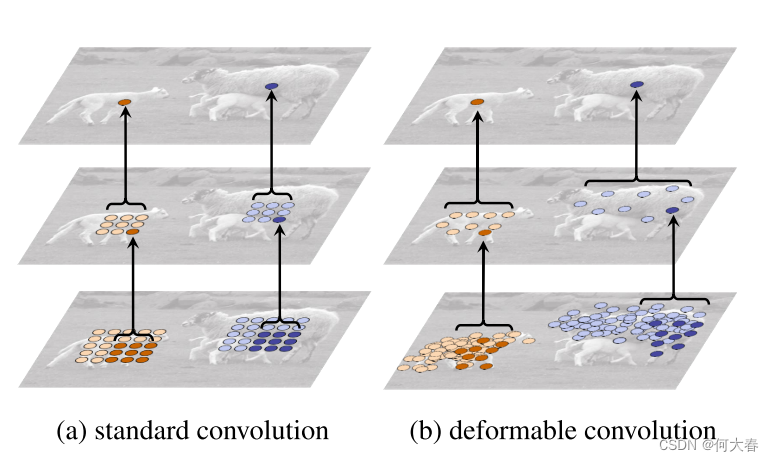
卷积不是固定的,由上图可知,每个点的感受范围不再是一个正方形的3x3的范围,而是“不规则”的卷积,当然,这个不规则是通过训练而学习得到的,在原来的基础上学习到了偏移量,就使卷积变成可形变的卷积了。









![[计算机网络] 当输入网址到网页](https://img-blog.csdnimg.cn/direct/a7d5320262c5455b9d45b4620c23c4f1.png)
