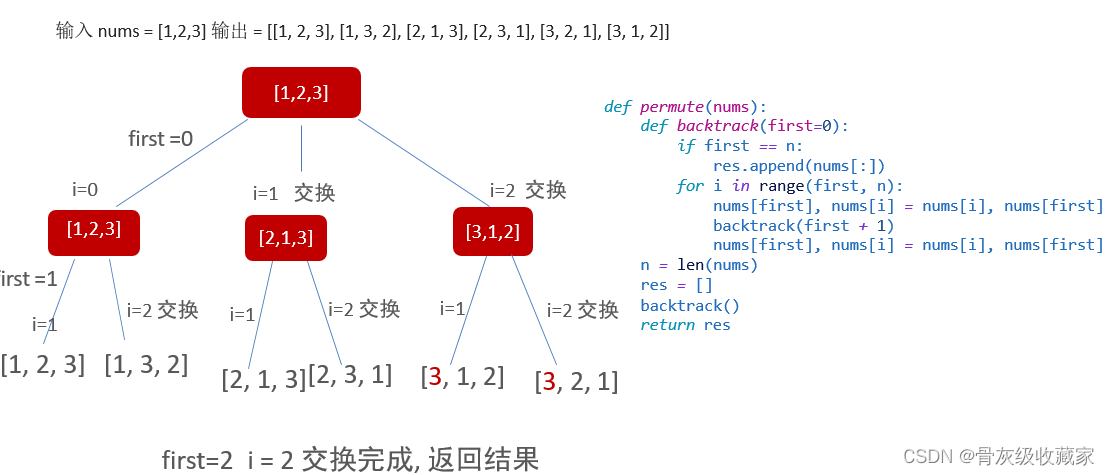
1. 链表
- 线性表的链式存储结构就是用一组任意的存储单元(可以是不连续的)存储线性表的数据元素。
- 采用链式存储结构的表示的线性表简称链表。
- 链式存储方式可用于表示线性结构,也可用于表示非线性结构。
链表通常有两个域
- data域——存放结点值的数据域
- next域——存放结点的直接后继的地址,需要指针类型表示

2.单链表的表示方式
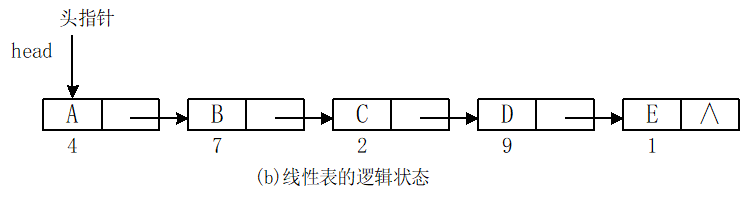
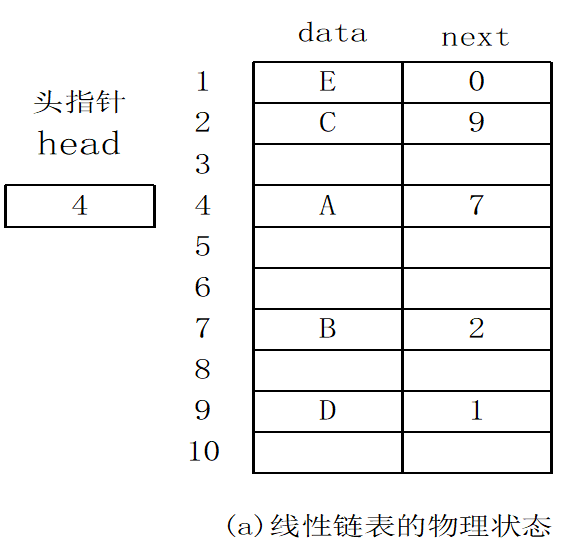
3.链表的存储结构
- 由于线性表中各元素间存在着线性关系,每一个元素有一个直接前驱和一个直接后继。
- 用链式存储结构表示线性表中的一个元素时至少需要两部分信息,一部分用于存放数据元素值,称为数据域;另一部分用于存放直接前驱或直接后继结点的地址(指针),称为指针域,称这种存储单元为结点。
4.链表的分类
- 单链表:只设置一个指向后继结点地址的指针域;
- 循环链表:链表首尾相接构成一个环状结构;
- 双向链表:单链表中增加一个指向前驱的指针。
5.单链表的基本运算与实现示例

#include"stdio.h"
#include"malloc.h"
typedef struct
{
int no;
int score;
}DataType;
typedef struct node
{
DataType data;
struct node *next;
}ListNode;
//线性表的创建 //头插法
ListNode * CreatList()
{
ListNode *L,*q;
DataType x; //x为dataType类型的结构体变量
L=(ListNode *)malloc(sizeof(ListNode)); //头结点
L->next=NULL;
printf("请输入学号和成绩,以学号-1为结束:\n");
scanf("%d",&x.no);
while(x.no!=-1)
{
scanf("%d",&x.score);
q=(ListNode *)malloc(sizeof(ListNode));
q->data=x;
q->next=L->next; //头结点所存地址保存于新建结点的指针域中//
L->next=q; //新建结点的地址保存于头结点的指针域中
scanf("%d",&x.no);
}
return L;
}
//初始化
ListNode * InitList()
{
ListNode *L;
L=(ListNode*)malloc(sizeof(ListNode));
L->next=NULL;
return L;
}
void PrintList(ListNode * L)
{
ListNode *p;
p=L->next;
while(p!=NULL)
{
printf("[%d,%d]\n",p->data.no,p->data.score);
p=p->next;
}
printf("\n");
}
int GetLength(ListNode *L)
{
int num=0;
ListNode *p;
p=L->next;
while(p!=NULL)
{ num++;
p=p->next;
}
return(num);
}
void InsertList(ListNode *L,int i,DataType x)
{
ListNode *p,*q,*s;
int j=1;
p=L;
if(i<1||i>GetLength(L)+1)
printf("error!\n");
s=(ListNode *)malloc(sizeof(ListNode));
s->data=x;
while(j<=i)
{
q=p;
p=p->next;
j++;
} /*找到插入位置*/
s->next=q->next;//=p
q->next=s;
}
//按序号取元素
ListNode *GetNode(ListNode *L,int i)
{
ListNode *p;
int j=1;
if(i<1 || i>GetLength(L))
{
printf("error!\n");
}
p=L->next;
while(p!=NULL&&j<i)
{
p=p->next;
j++;
}
return p;
}
//查找运算
int LocateList(ListNode *L,DataType x)
{
int k=1;
ListNode *p;
p=L->next;
while(p&&p->data.no!=x.no)
{
p=p->next;
k++;
}
if(p==NULL)
return 0;
else
return k;
}
//修改第i个元素
void EditList(ListNode *p,int i,DataType e)
{
int k=1;
if(i<1 ||i>GetLength(p))
{
printf("position error\n");
}
while(k<=i)
{
p=p->next;
k++;
}
p->data=e;
}
void DeleteList(ListNode *L,int i)
{
ListNode *p,*q;
int j=1;
p=L;
if(i<1 || i>GetLength(L))
{
printf("error!\n");
}
while(j<i)
{
p=p->next;
j++;
}
q=p->next;
p->next=q->next;
free(q);
}
//排序
void SortList(ListNode *L)
{
ListNode *p,*q,*pmin;
DataType e;
for(p=L->next;p->next!=NULL;p=p->next) //选择排序
{
pmin=p;
for(q=p->next;q!=NULL;q=q->next)
if(q->data.score>pmin->data.score)
pmin=q;
if(pmin!=p)
{
e=p->data;
p->data=pmin->data;
pmin->data=e;
}
}
}
void main()
{
ListNode *head,*p;
DataType e;
// head=InitList();
//创建
head=CreatList();
PrintList(head);
printf("The length of linklist is %d\n",GetLength(head));
//插入
e.no=9; e.score=80;
InsertList(head,GetLength(head)+1,e);
printf("插入后:\n");
PrintList(head);
printf("The length of linklist is %d\n",GetLength(head));
//查询
e.no=3;
int k=LocateList(head,e);
p=GetNode(head,k);
if(k>0)
printf("学号为3的记录:[%d %d]\n",p->data.no,p->data.score);
else
printf("不存在的\n");
//修改
e.no=3; e.score=100;
int m=LocateList(head,e);
EditList(head,m,e);
printf("修改后:\n");
PrintList(head);
//删除
e.no=2;
int n=LocateList(head,e);
DeleteList(head,n);
printf("删除学号为2的记录后:\n");
PrintList(head);
printf("The length of linklist is %d\n",GetLength(head));
//排序
printf("排序后:\n");
SortList(head);
PrintList(head);
}
6.循环链表
在单链表中,最后一个结点的指针域为空。访问单链表中任何数据只能从链表头开始顺序访问,而不能进行任何位置的随机查询访问。如要查询的结点在链表的尾部则需遍历整个链表。所以单链表的应用受到一定的限制。对单链表进行改进:
它将单链表中最后一个结点的指针指向链表的头结点,使整个链表头尾相接形成一个环形。
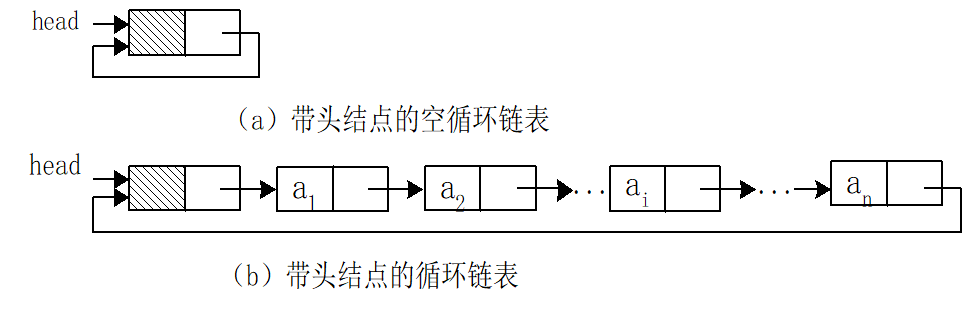
7.双向链表
双向链表用两个指针表示结点间的逻辑关系。 其增加了一个指向直接前驱的指针域,这样形成的链表有两条不同方向的链,前驱和后继,因此称为双链表。
双向链表结点的结构:
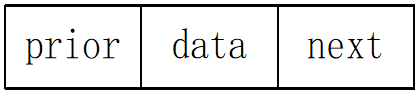
双向链表结点的定义如下:
typedef struct dlistnode{
DataType data;
struct dlistnode *prior,*next;
}DListNode;
双向链表结构示意图:
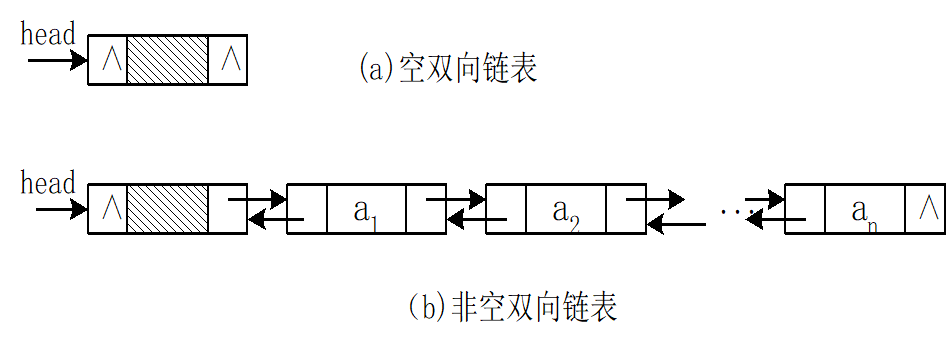
双向链表的插入操作:

关键语句指针操作序列既不是唯一也不是任意的。操作①必须在操作③之前完成,否则*p的前驱结点就丢掉了。
双向链表的删除操作:
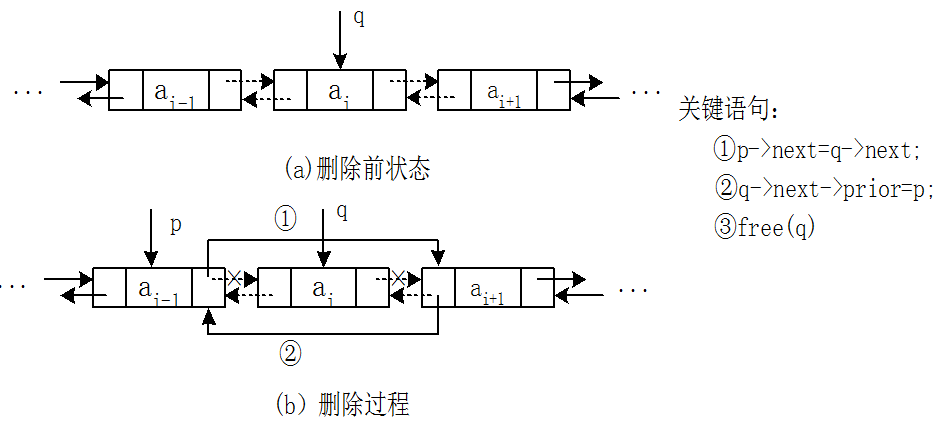
另一种写法:
void DDeleteNode(DListNode *p)
{
p->prior->next = p->next;
p->next->prior = p->prior;
free(p);
}补:循环双链表
循环链表+双向链表的结合
带头结点且有n个结点的循环双链表
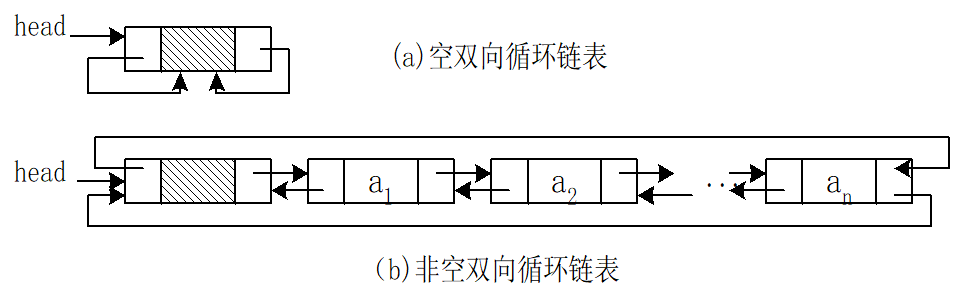
链式存储结构的特点:
优点:
- 结点空间可以动态申请和释放;
- 它的数据元素的逻辑次序靠结点的指针来指示,进行数据插入或删除时不需要移动数据元素。
不足:
- 每个结点中的指针域需额外占用存储空间,当每个结点的数据域所占字节不多时,指针域所占存储空间的比重就显得很大;
- 链式存储结构是一种非随机存储结构。对任一结点的操作都要从指针链查找到该结点,这增加了算法的复杂度。