红黑树深度解析：RB-DELETE操作的理论与实践

news2024/11/28 6:28:58

红黑树深度解析：RB-DELETE操作的理论与实践

  • 一、前言
  • 二、红黑树的核心性质
  • 三、RB-DELETE的过程
  • 四、RB-DELETE的实现细节
  • 五、RB-DELETE的复杂性分析
  • 六、维护红黑树性质的重要性
  • 七、代码示例
    • 7.1 伪代码
    • 7.2 C代码示例
  • 八、结论

一、前言

在现代计算机科学中，红黑树作为一种高效的自平衡二叉搜索树，在众多领域扮演着重要角色。它的高效性源于其能够在插入和删除操作后快速恢复平衡，从而保持了对数据的高效访问。本文将深入探讨红黑树的删除操作——RB-DELETE，分析其过程、复杂性以及如何维护红黑树的五个关键性质。
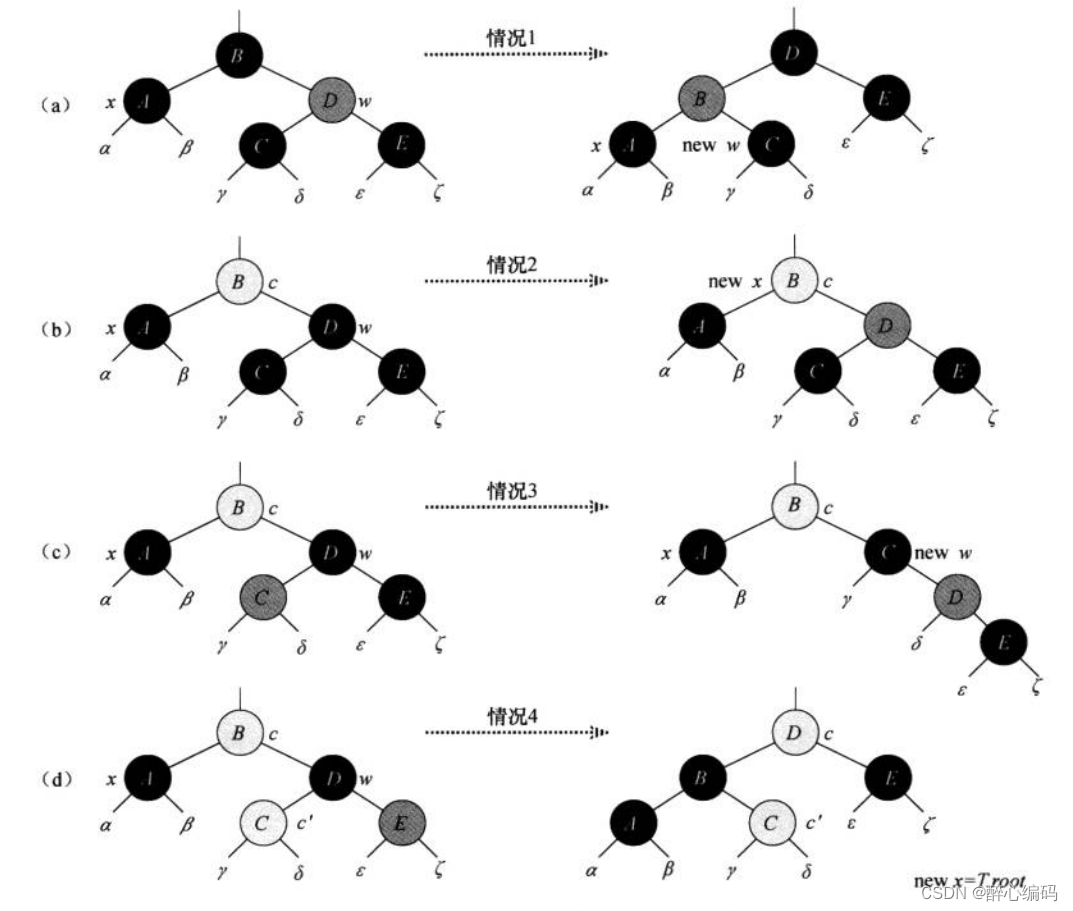
在这里插入图片描述

二、红黑树的核心性质

在深入了解RB-DELETE之前，我们必须回顾红黑树的五个核心性质：

  1. 性质1：每个结点要么是红色，要么是黑色。
  2. 性质2：根结点总是黑色的。
  3. 性质3：所有NIL结点（叶子结点）都是黑色的。
  4. 性质4：如果一个结点是红色的，则它的两个子结点都是黑色的（即红色结点不能相邻）。
  5. 性质5：从根结点到每个NIL结点的所有路径上，黑色结点的数量是相同的。

这些性质确保了红黑树在最坏情况下的平衡性，从而保证了操作的对数复杂度。

三、RB-DELETE的过程

RB-DELETE的过程是在红黑树中删除一个结点的步骤。与插入操作相比，删除操作更为复杂，因为它可能破坏上述性质。RB-DELETE的过程可以分为以下几个阶段：

  1. 找到并删除结点：首先，我们需要找到要删除的结点。如果结点有两个子结点，我们需要找到它的后继结点，并将其值复制到要删除的结点中。然后，我们实际上是在删除一个最多有一个子结点的结点。
  2. 替换和移植：接下来，我们需要用其后继结点或前驱结点替换要删除的结点。这个过程涉及到RB-TRANSPLANT操作，它会将替换结点的子结点移植到被删除结点的位置。
  3. 修正红黑性质：删除操作可能会破坏性质4和性质5。为了恢复这些性质，我们需要执行RB-DELETE-FIXUP过程，该过程通过重新着色和旋转来修复树。

四、RB-DELETE的实现细节

RB-DELETE的实现涉及到多个辅助函数，每个函数都有其特定的作用。以下是这些函数的简要描述：

  • RB-TRANSPLANT：这个函数将结点v移植到结点u的位置。它处理结点u的所有子结点，并更新它们的父指针。
  • TREE-MINIMUM：这个函数找到给定结点的最小后继结点，即没有更小关键字的子结点。
  • RB-DELETE-FIXUP：这个关键函数负责恢复红黑树的性质。它从被删除结点的位置开始，向上遍历树，直到根结点或遇到一个红色结点。

五、RB-DELETE的复杂性分析

RB-DELETE的复杂性主要取决于树的高度和删除操作后需要进行的修复工作。在最好的情况下，删除的结点没有子结点或者只有一个子结点，这时操作的时间复杂度是O(log n)。在最坏的情况下，删除的结点有两个子结点，我们需要找到其后继结点，并可能需要进行多次旋转和重新着色操作。尽管如此，RB-DELETE的总体复杂性仍然是O(log n)，这是因为红黑树的高度始终保持在O(log n)。

六、维护红黑树性质的重要性

在整个RB-DELETE过程中，维护红黑树的五个性质至关重要。这些性质不仅确保了树的平衡性，还保证了操作的效率。特别是性质4和性质5，它们在删除操作中最容易被破坏。RB-DELETE-FIXUP过程通过精心设计的旋转和重新着色步骤来修复这些性质，确保了树在删除操作后仍然保持平衡。

七、代码示例

为了更好地理解红黑树的删除操作，我们将首先提供RB-DELETE的完整伪代码，然后给出对应的C代码示例。

7.1 伪代码

RB-TRANSPLANT(T, u, v)
    if u.p == T.nil
        T.root = v
    else if u == u.p.left
        u.p.left = v
    else
        u.p.right = v
    if v != T.nil
        v.p = u.p

RB-DELETE(T, z)
    y = x
    y_original_color = y.color
    if z.left == T.nil
        x = z.right
        RB-TRANSPLANT(T, z, z.right)
    else if z.right == T.nil
        x = z.left
        RB-TRANSPLANT(T, z, z.left)
    else
        y = TREE-MINIMUM(z.right)
        y_original_color = y.color
        if y != y.p.left
            x = y.right
            RB-TRANSPLANT(T, y, y.right)
            y.right = z.right
            if y.right != T.nil
                y.right.p = y
        RB-TRANSPLANT(T, z, y)
        if y_original_color == BLACK
            RB-DELETE-FIXUP(T, x)

RB-DELETE-FIXUP(T, x)
    while x != T.root and x.color == BLACK
        if x == x.p.left
            w = x.p.right
            if w.color == RED
                w.color = BLACK
                x.p.color = RED
                LEFT-ROTATE(T, x.p)
                w = x.p.right
            if w.left.color == BLACK and w.right.color == BLACK
                parent_color = x.p.color
                x.p.color = BLACK
                w.left.color = BLACK
                w.right.color = BLACK
                x = T.root
            else if w.right.color == BLACK
                parent_color = x.p.color
                x.p.color = BLACK
                w.right.color = RED
                RIGHT-ROTATE(T, x.p)
                w = x.p.right
        else
            // Similar cases for x == x.p.right, with "left" and "right" exchanged
    x.color = BLACK
    T.root.color = BLACK

7.2 C代码示例

#include <stdio.h>
#include <stdlib.h>

// 假设已经有了红黑树结点的定义和相关操作的实现

// 定义旋转函数，这里只展示左旋作为示例
void LEFT_ROTATE(RedBlackTree T, Node *x) {
    Node *y = x->right;
    Node *Tnil = T->nil; // T->nil 是哨兵结点，始终为黑色

    // 执行旋转
    x->right = y->left;
    if (y->left != Tnil) {
        y->left->parent = x;
    }
    y->parent = x->parent;
    if (x->parent == T->root) {
        T->root = y;
    } else if (x == x->parent->left) {
        x->parent->left = y;
    } else {
        x->parent->right = y;
    }
    y->left = x;
    x->parent = y;
}

// RB-TRANSPLANT 函数的 C 语言实现
void RB_TRANSPLANT(RedBlackTree T, Node *u, Node *v) {
    if (u == T->root) {
        T->root = v;
    } else if (u == u->parent->left) {
        u->parent->left = v;
    } else {
        u->parent->right = v;
    }
    if (v != T->nil) {
        v->parent = u->parent;
    }
}

// RB-DELETE 函数的 C 语言实现
void RB_DELETE(RedBlackTree T, Node *z) {
    Node *y, *x, *Tnil = T->nil;
    Color y_original_color;

    if (z->left == Tnil) {
        x = z->right;
        RB_TRANSPLANT(T, z, z->right);
    } else if (z->right == Tnil) {
        x = z->left;
        RB_TRANSPLANT(T, z, z->left);
    } else {
        y = TREE_MINIMUM(z->right);
        y_original_color = y->color;
        if (y->right != Tnil) {
            x = y->right;
            RB_TRANSPLANT(T, y, y->right);
            y->right = z->right;
            if (y->right != Tnil) {
                y->right->parent = y;
            }
        }
        RB_TRANSPLANT(T, z, y);
        if (y->color == BLACK) {
            RB_DELETE_FIXUP(T, x);
        }
    }
}

// RB-DELETE-FIXUP 函数的 C 语言实现
void RB_DELETE_FIXUP(RedBlackTree T, Node *x) {
    Node *w, *parent;

    while (x != T->root && x->color == BLACK) {
        if (x == x->parent->left) {
            w = x->parent->right;
            if (w->color == RED) {
                w->color = BLACK;
                x->parent->color = RED;
                LEFT_ROTATE(T, x->parent);
                w = x->parent->right;
            }
            if (w->left->color == BLACK && w->right->color == BLACK) {
                parent->color = x->parent->color;
                x->parent->color = BLACK;
                w->left->color = BLACK;
                w->right->color = BLACK;
                x = T->root;
            } else if (w->right->color == BLACK) {
                parent->color = x->parent->color;
                x->parent->color = BLACK;
                w->right->color = RED;
                RIGHT_ROTATE(T, w);
                w = x->parent->right;
            }
        } else {
            // 类似的处理，但是是对于 x->parent->right 的情况
        }
    }
    x->color = BLACK;
    T->root->color = BLACK;
}

// 主函数或其他相关函数可以调用 RB_DELETE 来删除红黑树中的结点
int main() {
    // 红黑树的初始化和删除操作的代码
    // ...
    // 删除红黑树中的结点 z
    RB_DELETE(tree, z);
    // ...
    return 0;
}

在上述C代码中，我们定义了红黑树的旋转操作、RB-TRANSPLANT、RB-DELETE和RB-DELETE-FIXUP过程。注意，这里省略了一些细节，比如结点颜色的更改和旋转操作的具体实现，因为在实际应用中，这些操作需要结合具体的红黑树结点定义和内存管理来实现。

八、结论

通过上述代码，我们可以看到RB-DELETE过程中的详细步骤，以及如何通过RB-DELETE-FIXUP来修复删除操作可能破坏的红黑树性质。这些代码示例为理解和实现红黑树的删除操作提供了一个清晰的框架。

红黑树的RB-DELETE操作是数据结构领域的一个重要研究课题。通过本文的分析，我们可以看到，尽管删除操作比插入操作更为复杂，但通过精心设计的算法和辅助函数，我们可以有效地维护红黑树的平衡性和效率。RB-DELETE的实现不仅展示了红黑树的强大功能，也体现了计算机科学家在设计自平衡数据结构方面的智慧和创造力。随着计算机科学的发展，红黑树及其变种将继续在各种应用中发挥重要作用。

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1577005.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

备忘，LangChain建立本地知识库的几个要点

备忘，LangChain建立本地知识库的几个要点

本地知识库可以解决本地资源与AI结合的问题&#xff0c;为下一步应用管理已有资产奠定基础。 本地知识库的建立可参考LangChain结合通义千问的自建知识库 &#xff08;二&#xff09;、&#xff08;三&#xff09;、&#xff08;四&#xff09; 本文主要记录两个方面的问题 1 搭…
阅读更多...
抖音引流私域转化模式1.0现场视频，从抖音源源不断把人加到私域买单

抖音引流私域转化模式1.0现场视频，从抖音源源不断把人加到私域买单

抖音-引流私域转化模式1.0现场视频&#xff0c;从抖音源源不断把人加到私域&#xff0c;让加到私域的粉丝买单 课程内容&#xff1a;抖音引流私域转化模式1.0现场视频&#xff0c;从抖音源源不断把人加到私域买单 - 百创网-源码交易平台_网站源码_商城源码_小程序源码 01.第一…
阅读更多...
武汉星起航：运营经验打造行业标杆，形成可持续稳健业务增长路径

武汉星起航：运营经验打造行业标杆，形成可持续稳健业务增长路径

在跨境电商的浪潮中&#xff0c;武汉星起航电子商务有限公司以其专注于提供一站式解决方案而在行业内崭露头角&#xff0c;成为创业者成功进入市场的得力伙伴。公司不仅仅是服务提供商&#xff0c;更是创业者的导航者&#xff0c;通过全方位的支持和专业指导&#xff0c;致力于…
阅读更多...
javaWeb影视创作论坛的设计与实现

javaWeb影视创作论坛的设计与实现

摘要 随着时代的发展&#xff0c;互联网的出现&#xff0c;给传统影视行业带来的最大便利就是&#xff0c;方便了影视从业人员以及爱好者的交流和互动&#xff0c;而为用户提供一个书写影评&#xff0c;阅读影评以及回复影评的平台&#xff0c;以影评为载体来使用户感受影评、…
阅读更多...
android-自定义TextView在文字内容末尾添加图片icon、可以添加间距

android-自定义TextView在文字内容末尾添加图片icon、可以添加间距

样式示意图 自定义属性 style.xml <declare-styleable name"IconLabelTextView"><attr name"iconSrc" format"reference"/><attr name"iconPaddingStart" format"dimension"/><attr name"iconPad…
阅读更多...
小红不想做模拟题 线段树

小红不想做模拟题 线段树

无脑线段树 #include<iostream> using namespace std; const int N 1e510; int a[N],b[N];struct Segment{int l,r;int s,s1,s2;int lz1,lz2; }tr[N<<2];void pushdown(int u){if(tr[u].lz1){tr[u<<1].lz1 tr[u<<1|1].lz1 1;tr[u].lz1 0;tr[u<&…
阅读更多...
2024/4/1—力扣—两数相除

2024/4/1—力扣—两数相除

代码实现&#xff1a; 思路&#xff1a;用减法模拟除法 // 用减法模拟除法 int func(int a, int b) { // a、b均为负数int ans 0;while (a < b) { // a的绝对值大于等于b&#xff0c;表示此时a够减int t b;int count 1; // 用来计数被减的次数// t > INT_MIN / 2:防止…
阅读更多...
ArcGISPro 如何升级某项Python库且不影响其运行

ArcGISPro 如何升级某项Python库且不影响其运行

升级包scipy 可以看出scipy当前版本是1.6.2 利用不依赖包升级 pip install --upgrade scipy --no-deps 结果 但是显示还是之前的版本
阅读更多...
使用高德微信小程序插件实现精准获取打卡位置

使用高德微信小程序插件实现精准获取打卡位置

由于微信小程序的 getFuzzyLocation 误差太大 不得不改用高德微信sdk 使用方法&#xff1a; 一、下载 sdk 相关下载-微信小程序插件 | 高德地图API 二、引入 sdk //引入 var amapFile require(../../libs/amap-wx.js); Page({onLoad: function() {var that this;va…
阅读更多...
go的orm框架-Gorm

go的orm框架-Gorm

官网文档 特点 全功能 ORM 关联 (拥有一个&#xff0c;拥有多个&#xff0c;属于&#xff0c;多对多&#xff0c;多态&#xff0c;单表继承) Create&#xff0c;Save&#xff0c;Update&#xff0c;Delete&#xff0c;Find 中钩子方法 支持 Preload、Joins 的预加载 事务&…
阅读更多...
Vue.js【组件基础（上）】

Vue.js【组件基础（上）】

选项式API和组合式API 选项式API 选项式API是一种通过包含多个选项的对象来描述组件逻辑的API&#xff0c;其常用的选项包括data、methods、computed、watch等。 组合式API 相比于选项式API&#xff0c;组合式API是将组件中的数据、方法、计算属性、侦听器等代码全部组合在…
阅读更多...
sigmoid函数实例

sigmoid函数实例

sigmoid实例案例&#xff1a;&#xff08;sigmoid作用就是把传统线性回归中的z 投射到分类问题&#xff08;0&#xff0c;1&#xff09;的概率中&#xff09; 交叉熵损失函数扩充解释&#xff1a; 为什么二分类和多分类的不一样 因为在二分类问题中 每个样本得值是0或1 一组数据…
阅读更多...
使用spring模拟转账，并实现异常事务回滚

使用spring模拟转账，并实现异常事务回滚

1、数据库准备 使用配置类配置数据源、模板、事务回滚 package cn.edu.aaa.utils;import java.beans.PropertyVetoException;import javax.sql.DataSource;import org.springframework.beans.factory.annotation.Autowired; import org.springframework.beans.factory.annotati…
阅读更多...
iterrows方法使dataframe显示完整

iterrows方法使dataframe显示完整

这样一个excel文件&#xff0c;由于行数太多显示不全。 直接读取显示&#xff1a; 该如何处理&#xff1f;方法有很多&#xff0c;这次讲解用dataframe.iterrows()方法。 DataFrame.iterrows()方法&#xff1a; 返回值是一个由索引和Series组成的元组。 关于这个方法的两个注…
阅读更多...
程序汪10万接的多平台视频分发项目，模拟人工发视频

程序汪10万接的多平台视频分发项目，模拟人工发视频

本项目来自程序汪背后的私活小团队&#xff0c;开发了一个多平台分发视频项目&#xff0c;给粉丝分享一下解决方案和具体项目分开情况付款情况等等细节&#xff0c;希望给想接私活的朋友一些经验参考 程序汪10万接的多平台视频分发项目&#xff0c;模拟人工发视频 视频版本 在 …
阅读更多...
【网站项目】自助购药小程序

【网站项目】自助购药小程序

&#x1f64a;作者简介&#xff1a;拥有多年开发工作经验&#xff0c;分享技术代码帮助学生学习&#xff0c;独立完成自己的项目或者毕业设计。 代码可以私聊博主获取。&#x1f339;赠送计算机毕业设计600个选题excel文件&#xff0c;帮助大学选题。赠送开题报告模板&#xff…
阅读更多...
VSCODE目录树缩进调整

VSCODE目录树缩进调整

VSCode默认的缩进太小了&#xff0c;简直看不出来&#xff0c;很容易弄混目录。在设置里修改就行了。 修改后效果&#xff1a;
阅读更多...
代码随想录算法训练营第48天|198.打家劫舍|213.打家劫舍II| 337.打家劫舍III

代码随想录算法训练营第48天|198.打家劫舍|213.打家劫舍II| 337.打家劫舍III

代码随想录算法训练营第48天|198.打家劫舍|213.打家劫舍II| 337.打家劫舍III 今天就是打家劫舍的一天&#xff0c;这个系列不算难&#xff0c;大家可以一口气拿下。 198.打家劫舍 视频讲解&#xff1a;https://www.bilibili.com/video/BV1Te411N7SX https://programmercarl.c…
阅读更多...
合并主分支到子分支

合并主分支到子分支

参考&#xff1a;【Git】合并分支出现 Please enter a commit message to explain why this merge is necessary.-CSDN博客 git 如何将主分支(master)合并到子分支上_git 将主分支合并到子分支-CSDN博客 1、先切换到主分支master git checkout master 2、把主分支代码拉到本地…
阅读更多...
T-Mamba：用于牙齿 3D CBCT 分割的频率增强门控长程依赖性

T-Mamba：用于牙齿 3D CBCT 分割的频率增强门控长程依赖性

T-Mamba&#xff1a;用于牙齿 3D CBCT 分割的频率增强门控长程依赖性 摘要Introduction方法T-Mamba architectureTim block T-Mamba: Frequency-Enhanced Gated Long-Range Dependendcy for Tooth 3D CBCT Segmentation 摘要 三维成像中的高效牙齿分割对于正畸诊断至关重要&am…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023