3D渲染器原理及Python朴素实现

最近，我发现自己需要为即将进行的项目提供一些来自不同角度的低多边形 3D 模型的低分辨率精灵。像这样的东西：

获得它们的可能方法包括：

学习一点 Blender
在 WebGL 中制作
编写我自己的渲染器

我对 Blender 的短暂经历已经让我受到了创伤，而且 WebGL 的 API 有点令人困惑。还有什么比在我自己的 3D 引擎中进行一些 3D 变换更好的机会来温习线性代数呢？

这是 Github 存储库的链接。

NSDT工具推荐： Three.js AI纹理开发包 - YOLO合成数据生成器 - GLTF/GLB在线编辑 - 3D模型格式在线转换 - 可编程3D场景编辑器 - REVIT导出3D模型插件 - 3D模型语义搜索引擎 - Three.js虚拟轴心开发包 - 3D模型在线减面 - STL模型在线切割

1、3D 对象是如何表示的

3D 图形超简短介绍：所有 3D 对象都由 3D 空间中的三角形表示。这意味着每个三角形由 3 个点组成，每个点包含 3 个变量：x、y 和 z。

我们的目标是将这些点、颜色等的数组转换为漂亮的 .png 图片，我们可以将其用作精灵。

你看到的大多数 3D 图形都是透视投影，因此距离相机较远的物体看起来较小。但我们只会关注并非如此的正交投影。无论物体距离相机有多远，它的大小都不会改变。

所以我们将在这里构建的是：

✔️ 功能强大的 3D 渲染器，可调节相机方向
✔️ Z 缓冲可准确表示重叠三角形
✔️基本定向着色

我们不会介绍的内容（至少目前）：

❌物体投射到其他物体上的阴影
❌ 纹理化
❌透视投影

而且它也不能在 GPU 上运行。效率不会很高。实时渲染复杂的场景（甚至可能是简单的场景）是不够的。但这会很有趣并且令人满意，至少对我来说是这样。

2、第一张图片

安装依赖项，我们将使用 numpy 进行矩阵运算，并使用 Pillow 将数组转换为图像。

pip install Pillow numpy

在 renderer.py 文件中创建 Object3D 类来存储各个模型。

# renderer.py

import numpy as np
from PIL import Image


class Object3D:
    def __init__(self, points, triangles, colors):
        self.points = points
        self.triangles = triangles
        self.colors = colors

points：包含 3D 对象中点坐标的数组
triangles：包含组成三角形的点索引的数组
colors：每个三角形的 RGB 值数组（例如白色 = [255, 255, 255]）

渲染器类：

# renderer.py

class Renderer:
    def __init__(
        self,
        objects,
        viewport,
        resolution,
        camera_angle=0.0,
        camera_pitch=0.0,
    ):
        self._objects = objects
        self._viewport = viewport
        self._resolution = resolution
        self._camera_angle = camera_angle
        self._camera_pitch = camera_pitch

        resolution_x, resolution_y = self._resolution
        self._screen = np.ones((resolution_y, resolution_x, 3), "uint8") * 120

        x_min, y_min, x_max, y_max = self._viewport
        self._range_x = np.linspace(x_min, x_max, resolution_x)
        self._range_y = np.linspace(y_max, y_min, resolution_y)

    def render_scene(self, output_path):
        for object_3d in self._objects:
            self._render_object(object_3d)
        im = Image.fromarray(self._screen)
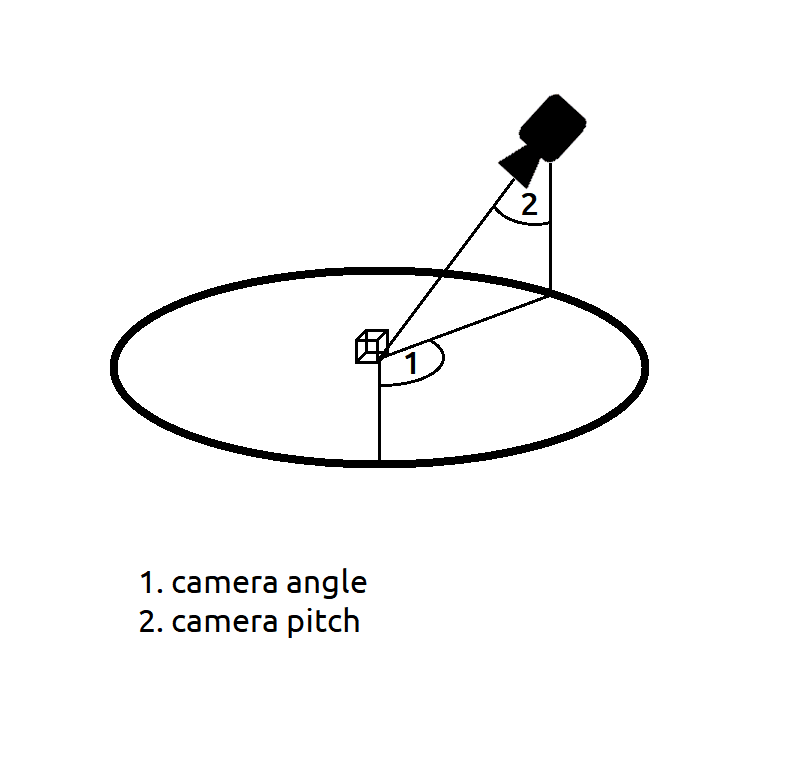
        im.save(output_path)

_objects：场景中的 3D 对象列表
_viewport：可见区域，形式为（min_x，min_y，max_x，max_y）
_resolution：输出图像分辨率，(80, 48) 表示图像宽 80px，高 48px。
_camera_angle 和 _camera_pitch 定义相机的位置和方向，如下图所示
_screen：表示输出图像的RGB位图的数组
_range_x， _range_y：表示每行/每列像素的 x 和 y 世界坐标的数组

到目前为止，没有什么太花哨的。现在我们将实现 _render_object。

# renderer.py

class Renderer:
    ...
    def _render_object(self, object_3d):
        projected_points = self._get_object_projected_points(object_3d)
        projected_triangles = projected_points[object_3d.triangles]

        for triangle_points, color in zip(projected_triangles, object_3d.colors):
            self._render_triangle(triangle_points, color)

首先，我们需要使用 _get_object_projected_points 将世界坐标转换为相机坐标：

class Renderer:
    ...
    def _get_object_projected_points(self, object_3d):
            return (
                object_3d.points
                @ _get_z_rotation_matrix(self._camera_angle)
                @ _get_x_rotation_matrix(self._camera_pitch)
            )


def _get_x_rotation_matrix(angle):
    return np.array(
        [
            [1, 0, 0],
            [0, np.cos(angle), -np.sin(angle)],
            [0, np.sin(angle), np.cos(angle)],
        ]
    )


def _get_z_rotation_matrix(angle):
    return np.array(
        [
            [np.cos(angle), -np.sin(angle), 0],
            [np.sin(angle), np.cos(angle), 0],
            [0, 0, 1],
        ]
    )

为此，我们首先在 Z 轴上将对象坐标旋转 _camera_angle，然后在 X 轴上旋转 _camera_pitch。你可以在维基百科上找到每个轴的旋转矩阵。

现在让我们编写一个渲染单个三角形的方法：

# renderer.py

class Renderer:
    ...
    def _render_triangle(self, points, color):
        bounding_box = _get_bounding_box(points)

        for screen_x, scene_x in enumerate(self._range_x):
            if scene_x < bounding_box[0, 0] or scene_x > bounding_box[1, 0]:
                continue
            for screen_y, scene_y in enumerate(self._range_y):
                if scene_y < bounding_box[0, 1] or scene_y > bounding_box[1, 1]:
                    continue
                if not _point_in_triangle(np.array([scene_x, scene_y, 0]), points):
                    continue
                self._screen[screen_y, screen_x, :] = color


def _get_bounding_box(points):
    return np.array(
        [
            [np.min(points[:, 0]), np.min(points[:, 1])],
            [np.max(points[:, 0]), np.max(points[:, 1])],
        ]
    )

screen_x：[0，分辨率[0]]范围内的整数
scene_x：在范围 [视口 [0]，视口 [2]] 内浮动

如果当前点不在三角形的边界框内，我们将迭代每个像素并跳过。否则，我们检查点是否在三角形内，如果是，则对当前像素着色。

检查点是否在三角形内实际上并不是一个小问题。我从这个 stackoverflow 帖子中复制粘贴了解决方案。

# renderer.py

def _sign(p1, p2, p3):
    return (p1[0] - p3[0]) * (p2[1] - (p3[1])) - (p2[0] - p3[0]) * (p1[1] - p3[1])


def _point_in_triangle(p, triangle):
    a, b, c = triangle
    d1 = _sign(p, a, b)
    d2 = _sign(p, b, c)
    d3 = _sign(p, c, a)

    has_neg = (d1 < 0) or (d2 < 0) or (d3 < 0)
    has_pos = (d1 > 0) or (d2 > 0) or (d3 > 0)

    return not (has_neg and has_pos)

无需过多讨论细节，我们检查该点是否位于由三角形顶点构造的三个半平面中的每一个的同一侧。如果是，则表示该点在三角形内。此方法适用于顺时针和逆时针三角形。

现在让我们创建一个简单的场景并在 main.py 中渲染它：

# main.py

import numpy as np

from renderer import Renderer, Object3D

WHITE = [255, 255, 255]
YELLOW = [200, 200, 0]
GREEN = [0, 200, 0]
BLUE = [0, 0, 200]
RED = [200, 0, 0]
ORANGE = [200, 100, 0]


cube_points = np.array(
    [
        [-1, -1, -1],
        [-1, 1, -1],
        [1, 1, -1],
        [1, -1, -1],
        [-1, -1, 1],
        [-1, 1, 1],
        [1, 1, 1],
        [1, -1, 1],
    ]
)

cube_triangles = np.array(
    [
        # bottom
        [0, 2, 1],
        [0, 3, 2],
        # top
        [4, 5, 6],
        [4, 6, 7],
        # back
        [1, 2, 6],
        [1, 6, 5],
        # front
        [0, 4, 7],
        [0, 7, 3],
        # left
        [0, 1, 5],
        [0, 5, 4],
        # right
        [3, 7, 6],
        [3, 6, 2],
    ]
)

cube_colors = np.array(
    [
        YELLOW,
        YELLOW,
        WHITE,
        WHITE,
        ORANGE,
        ORANGE,
        RED,
        RED,
        GREEN,
        GREEN,
        BLUE,
        BLUE,
    ]
)

cube = Object3D(cube_points, cube_triangles, cube_colors)

renderer = Renderer(
    [cube],
    (-2, -2, 2, 2),
    (300, 300),
    camera_angle=np.deg2rad(45),
    camera_pitch=np.deg2rad(60),
)
renderer.render_scene("scene.png")

让我们运行该脚本：

看起来还不像立方体，因为我们可以看到面是按某种随机顺序绘制的，并且以不可预测的方式相互重叠。

我们还可以看到绘制了橙色脸部（背面）和绿色脸部（左侧），尽管从相机方向看不到它们。 3D 引擎中的三角形只有一个可见边，以避免不必要的计算。我们将首先解决它。

3、删除不面向相机的三角形

让我们向 Renderer 添加另一个属性：

# renderer.py

class Renderer:
    def __init__(
        ...
    ):
        ...
        self._camera_dir = np.array([0, 0, -1])

并修改 _render_object：

class Renderer:
    ...
    def _render_object(self, object_3d):
        projected_points = self._get_object_projected_points(object_3d)
        projected_triangles = projected_points[object_3d.triangles]

        visible_mask = self._get_screen_dot_products(projected_triangles) < 0
        if not any(visible_mask):
            return

        for triangle_points, color in zip(
            projected_triangles[visible_mask], object_3d.colors[visible_mask]
        ):
            self._render_triangle(triangle_points, color)

    def _get_screen_dot_products(self, triangles):
        normals = np.cross(
            (triangles[:, 0] - triangles[:, 1]),
            (triangles[:, 2] - triangles[:, 1]),
        )
        return (self._camera_dir * normals).sum(axis=1)

我们如何知道三角形是否可见？

我们首先需要找到三角形的表面向量，它是向量 ab 和 ac 的叉积。

点积是衡量两个向量对齐程度的指标（根据它们指向的方向）。因此，让我们计算相机方向和三角形表面向量的点积。值小于 0 表示三角形可见，大于 0 表示不可见，0 表示两个向量垂直（也表示三角形不可见）。

现在运行脚本我们可以看到类似魔方的东西：

但我们的渲染器仍然缺乏一个非常基本的能力。如果我们尝试渲染彼此堆叠的三角形，我们将根据 Object3D.triangles 中定义的三角形的顺序获得结果。

尽管在摄像机和世界坐标中绿色三角形堆叠在红色三角形之上，但绿色三角形是在红色三角形之前绘制的。

我们可以找到一种方法对三角形进行排序，并按照从距离相机最远的到最近的顺序渲染它们。但对三角形进行排序实际上并不是一件容易的事。我们还会遇到两个或多个三角形相交的情况，或者在不将三角形分割成更小的三角形的情况下无法准确对三角形进行排序的情况。

4、✨Z 缓冲✨

这就是 Z 缓冲的用武之地。我们不是对整个三角形进行操作，而是计算位图上绘制的每个像素的 Z 值并将其存储在不同的数组中。每个单元格将被初始化为无穷大，然后在对像素`_screen` 着色之前，我们将比较三角形上当前点的深度和 _z_buffer 数组中该像素的存储深度。

如何计算三角形平面上已知X和Y坐标的点的Z坐标？我们需要求解简单的线性系统以获得 X 轴和 Y 轴上的 Delta Z 值。

对于三角形 ABC，我们首先计算向量 AB 和 AC。

v1 = B - A
v2 = C - A

然后，计算 Z：

v1.x + v1.y = v1.z
v2.x + v2.y = v2.z

代码如下：

# renderer.py

def _calculate_delta_z(points):
    v_ab = points[1] - points[0]
    v_ac = points[2] - points[0]
    slope = np.array([v_ab[:2], v_ac[:2]])
    zs = np.array([v_ab[2], v_ac[2]])
    return np.linalg.solve(slope, zs)

当我们有了 delta Z (dz) 并选择三角形的任意顶点 (a) 时，我们可以计算任意点 (p) 的深度：

v_pa = a - p
depth = a.z + v_pa * dz

让我们添加 z 缓冲区数组并修改 _render_triangle 方法：

# renderer.py

class Renderer:
    def __init__(
        ...
    ):
        ...
        self._z_buffer = np.ones((resolution_y, resolution_x)) * -np.inf

    ...
    def _render_triangle(self, points, color):
        bounding_box = _get_bounding_box(points)
        # np.linalg.solve can throw an error so we need to handle it
        try:
            delta_z = _calculate_delta_z(points)
        except np.linalg.LinAlgError:
            return

        for screen_x, scene_x in enumerate(self._range_x):
            if scene_x < bounding_box[0, 0] or scene_x > bounding_box[1, 0]:
                continue
            for screen_y, scene_y in enumerate(self._range_y):
                if scene_y < bounding_box[0, 1] or scene_y > bounding_box[1, 1]:
                    continue
                if not _point_in_triangle(np.array([scene_x, scene_y, 0]), points):
                    continue
                depth = (
                    points[0][2]
                    + (np.array([scene_x, scene_y]) - points[0][:2]) @ delta_z
                )
                if depth <= self._z_buffer[screen_y, screen_x]:
                    continue
                self._screen[screen_y, screen_x, :] = color
                self._z_buffer[screen_y, screen_x] = depth

现在，无论 Object3D.triangles 的顺序如何，堆叠的三角形都可以正确渲染。

渲染器仍然缺乏一项基本且美观的功能，那就是着色。目前，每个像素都使用为特定三角形定义的颜色进行着色。所以我们会添加定向照明来让渲染的图像更加赏心悦目。

5、基本定向照明

我们将使用与确定三角形是否可见的方式类似的方式来确定三角形获得的光线量。但这一次我们不仅需要知道点积是大于还是小于 0，还需要精确的值，因此我们将对单位向量进行操作，单位向量是单个长度单位的向量。要将向量转换为单位向量，你需要计算其长度，然后乘以 1/长度：

# 计算向量A的单位向量
length = sqrt(A.x^2 + A.y^2 + A.z^2)
unit_A = A * 1 / length

代码如下：

# renderer.py

def _normalize_vector(p):
    return 1 / np.sqrt((p**2).sum()) * p

这将产生 -1（指向相反方向）和 1（指向完全相同的方向）之间的值。

将光线方向作为属性添加到 Renderer 对象：

# renderer.py

class Renderer:
    def __init__(
        ...
    ):
        ...
        self._light_dir = _normalize_vector(np.array([1, -1, -1]))

    def _calculate_color(self, points, color):
        v_ba = points[0] - points[1]
        v_bc = points[2] - points[1]
        surface_unit_vector = _normalize_vector(np.cross(v_ba, v_bc))
        factor = 1 - (np.dot(self._light_dir, surface_unit_vector) + 1) / 2

        r, g, b = color
        r = int(factor * r)
        g = int(factor * g)
        b = int(factor * b)
        return np.array([r, g, b], "uint8")

我会将点积归一化为 [0, 1] 范围，并将 RGB 值乘以 1 减去它，但你可以使用更高级的函数来实现。

📢免责声明📢
我选择将光线的方向与相机的位置/方向绑定。要使其独立，你需要执行相同的步骤，但不使用三角形的投影点，而是使用其未变换的世界坐标。

现在让我们修改 _render_triangle：

class Renderer:
    ...
    def _render_triangle(self, points, color):
        shaded_color = self._calculate_color(points, color)
        ...
        for screen_x, scene_x in enumerate(self._range_x):
            ...
            for screen_y, scene_y in enumerate(self._range_y):
                ...
                self._screen[screen_y, screen_x, :] = shaded_color
                self._z_buffer[screen_y, screen_x] = depth

将立方体的颜色更改为白色以更好地看到差异：