一,快速排序
快速排序是一种比较复杂的排序算法,它总共有4种实现方式,分别是挖坑法,左右"指针"法,前后"指针"法,以及非递归的快速排序,并且这些算法中也会涉及多种优化措施,比如三数取中,小区间优化,下面都会一一介绍。
由于它效率极高的缘故,快速排序也是日常开发中使用最多的,最重要的排序算法。
1. 挖坑法
1.1 基本思想:
任取待排序元素序列中的某元素(一般选最左边或最右边的元素)作为基准值(也叫做 key 关键字),按照该排序码将待排序集合分割成两子序列,左子序列中所有元素均小于基准值,右子序列中所有元素均大于基准值,然后左右子序列重复该过程,直到所有元素都排列在相应位置上为止。
1.2 一趟排序图解如下:
给定一无序数组,选第一个元素为关键字 key = 6
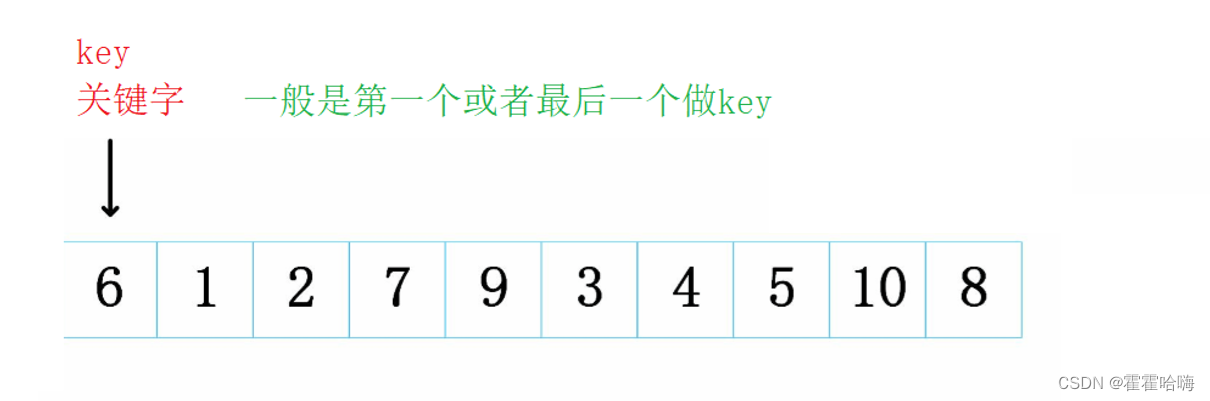
我们选定关键字 key = 6后,就说明6的位置就可以被覆盖了,所以我们就说左边形成了一个****坑,用pivot 表示。

左边有坑,右边的 end 要从最后一个元素开始找比 key 小的数,找到后放到左边的坑里,所以5放进了坑中
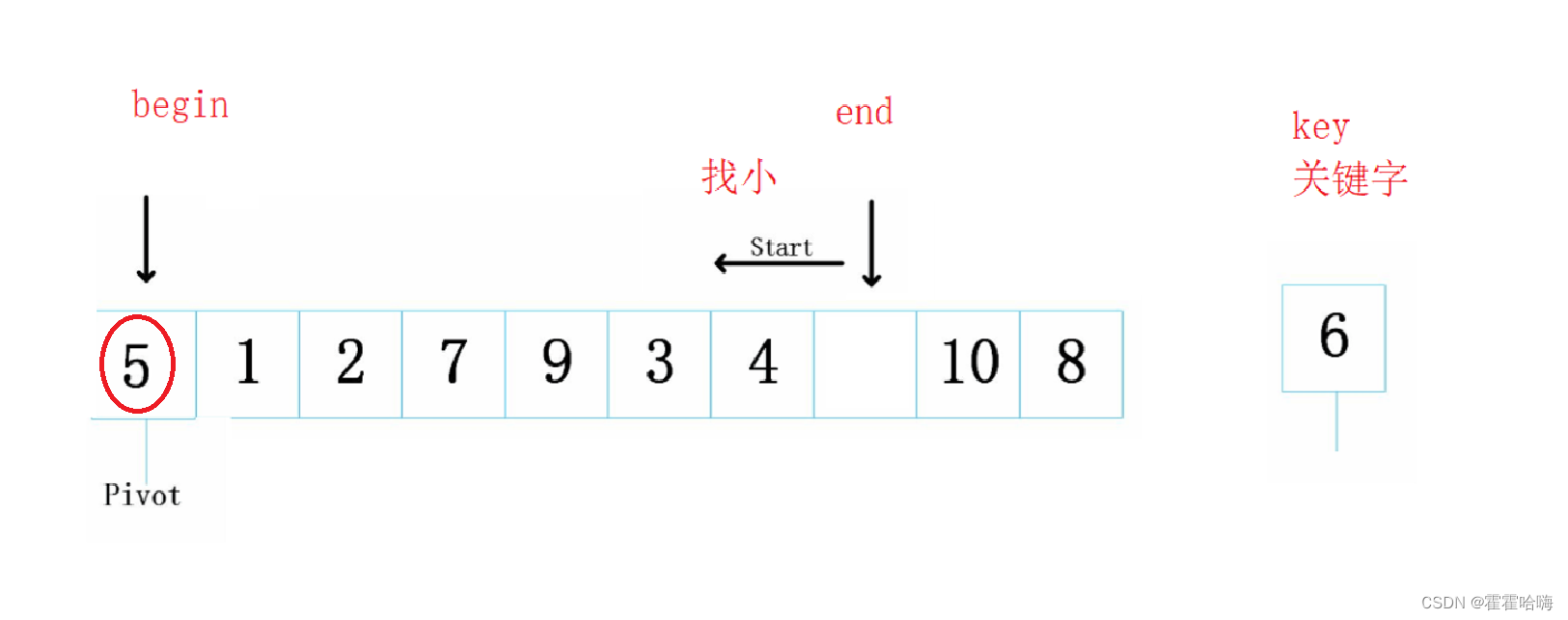
5被拿走之后,右边它原来所在的位置就形成了一个新坑,此时,左边的 begin 要开始找比 key 大的数,找到后放到右边的坑里,所以7放进了坑中
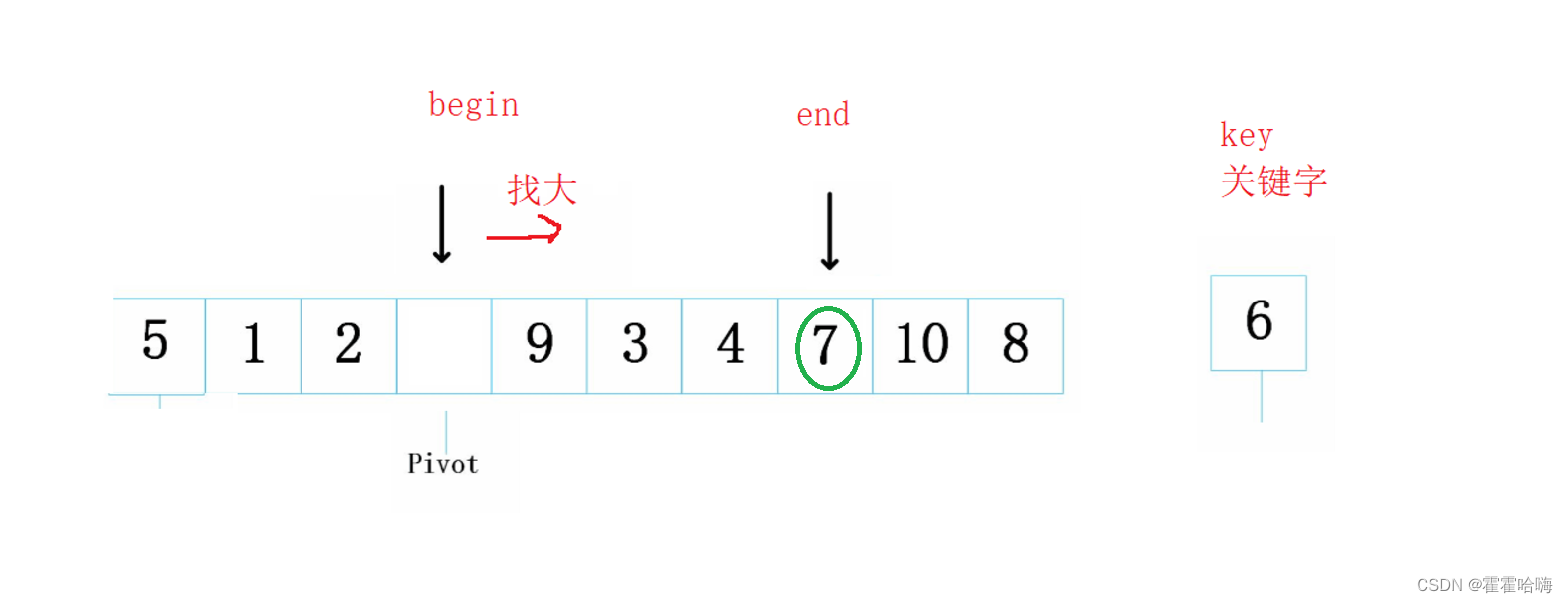
7被拿走后,左边又形成了一个新坑,此时,end 又要开始找比 key 小的数放到左边的坑里,所以4放进了坑中
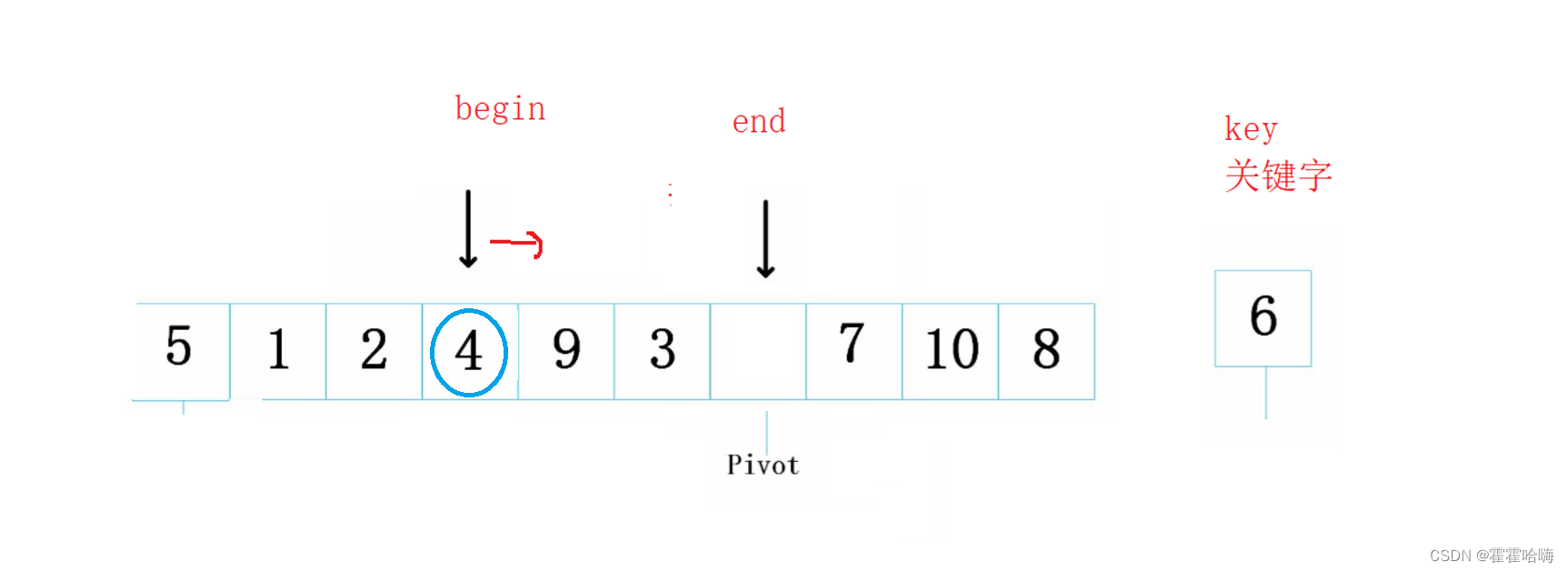
此时,右边又形成了新坑,begin 要开始找比 key 大的数,找到后放到右边的坑里,所以9放进了坑中
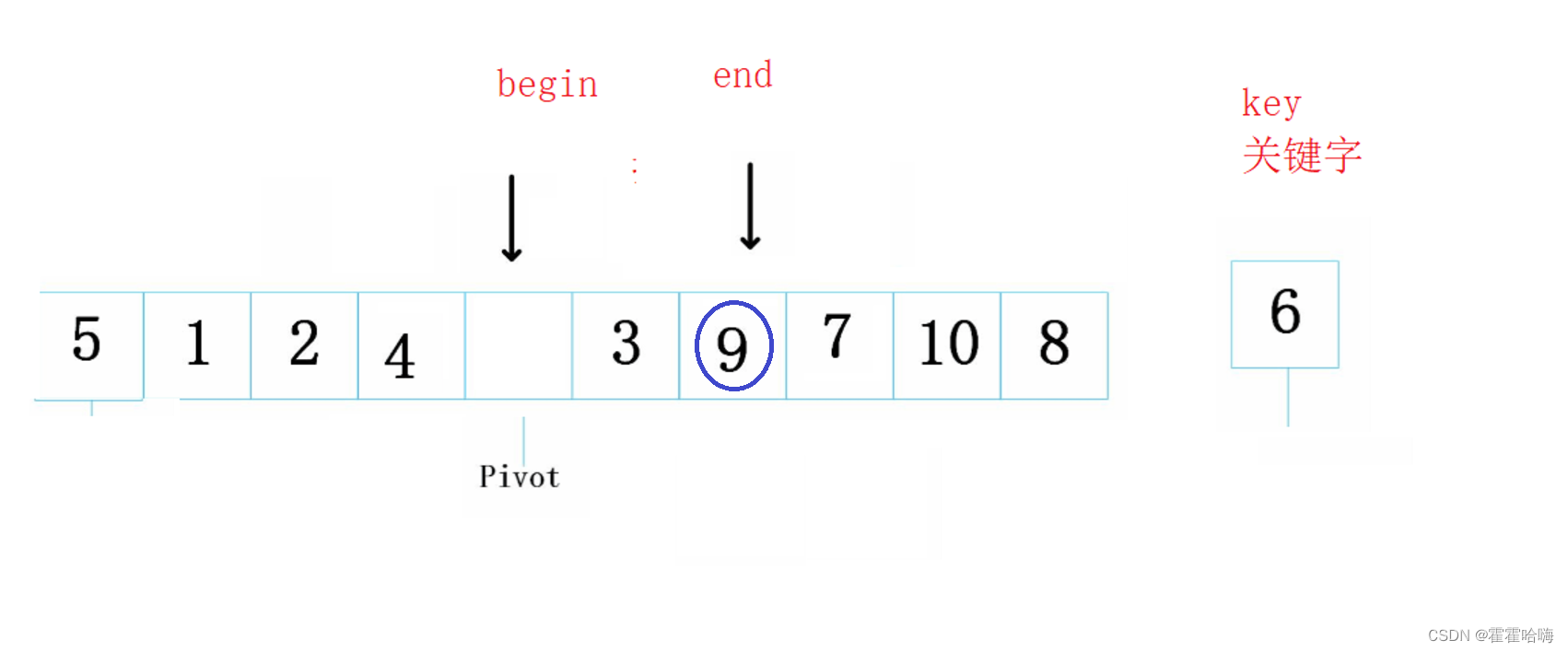
左边又形成了坑,右边 end 开始找,找到了3,放入坑中
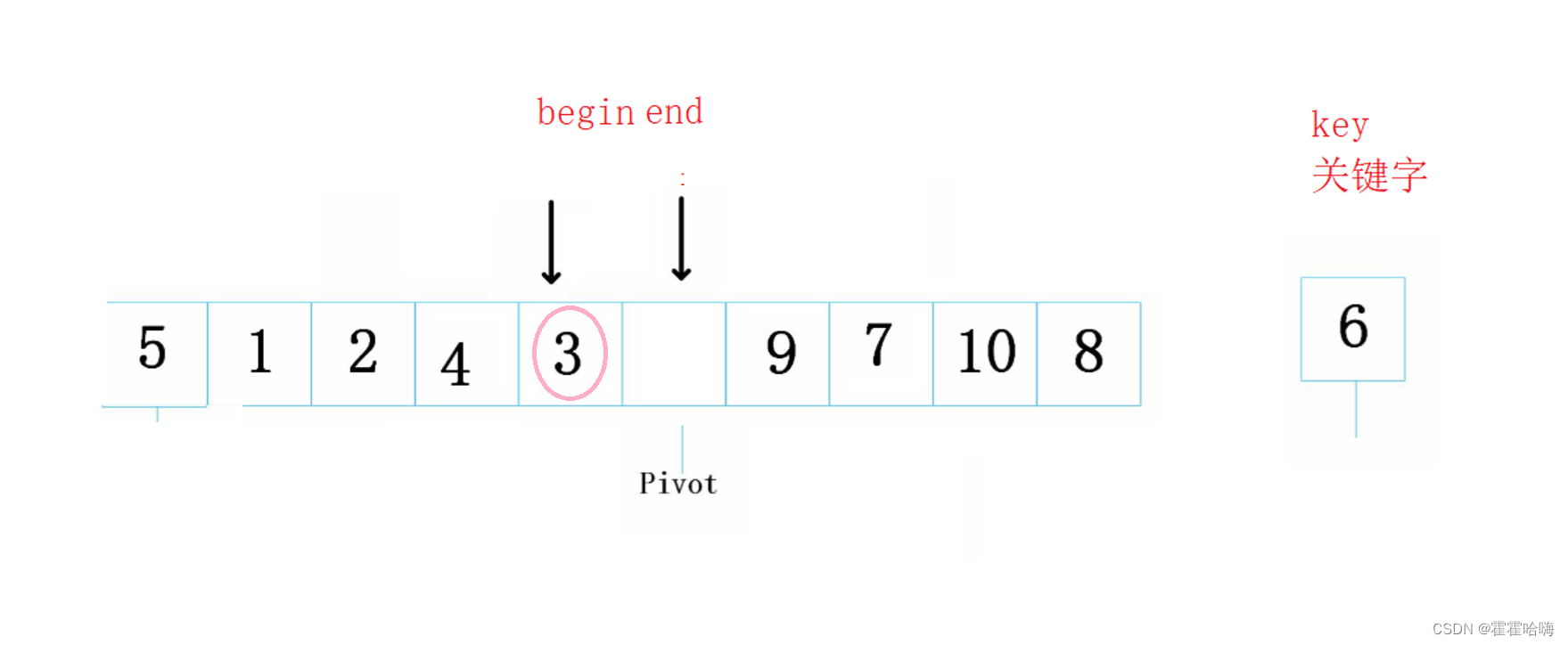
最后一次 begin++ 后,begin 和 end 重叠了,并且它们一定相遇在坑中,此时,把 key 放入坑中即可。
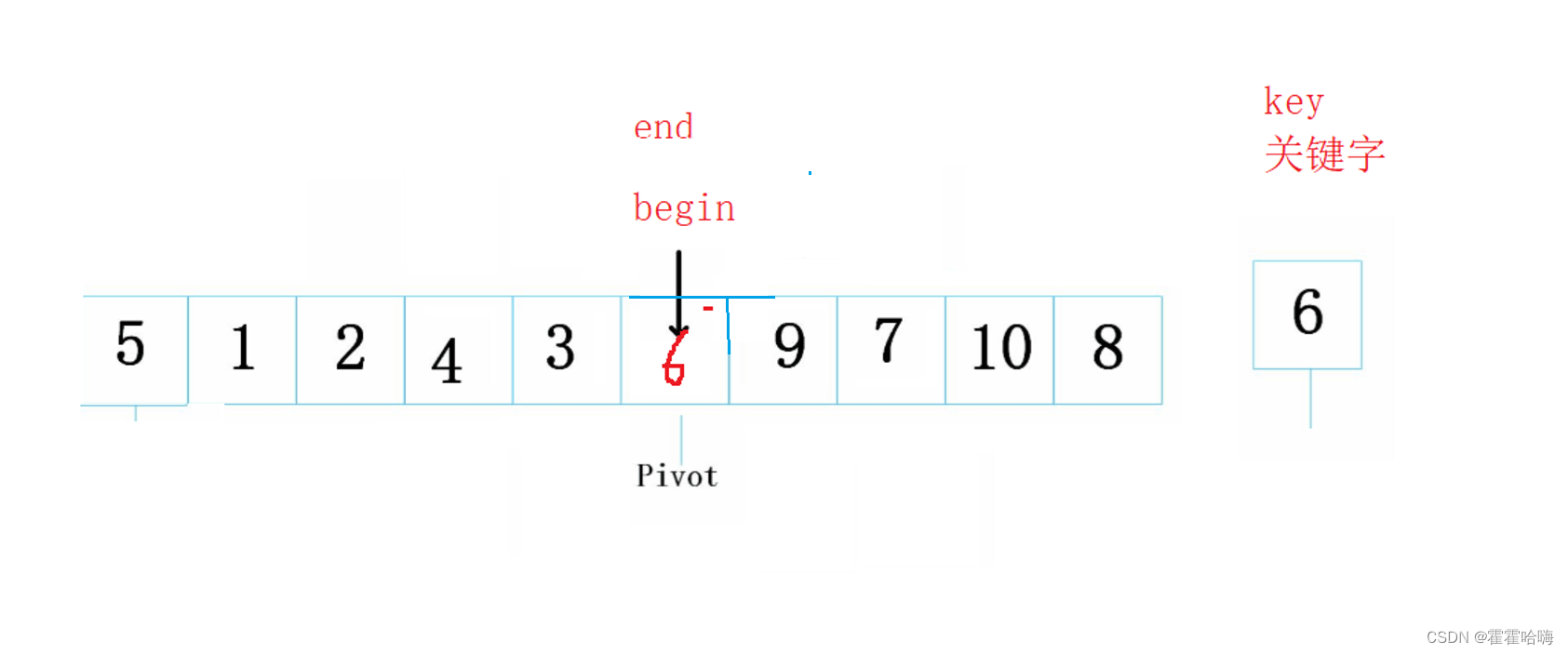
上述操作只是第一趟排序,只排好了一个数,此时第一个基准 key = 6已经在它合适的位置上了(排好序后的位置),后面对左右子序列排序时6不动。并且已经把数组分成了两个子序列,以 key 为基准,左边的元素都比它小,右边的元素都比它大。
1.3 单趟排序的代码实现如下:
注意:第二个和第三个 while 中的 begin < end 不能缺少,要防止在找大和找小的时候 begin 和 end 错开或是在极端情况下(比如已经升序时)end一直减导致越界。
int PartSort1(int* arr, int sz)
{
int begin = 0;
int end = sz -1;
int key = arr[begin];
int pivot = begin;
//这是排一趟,只排好了一个数
while (begin < end)
{
//左边有坑,右边end找比key小的
while (begin < end && arr[end] > key)
{
end--;
}
//小的放到了左边的坑里,右边end自己形成了新的坑
arr[pivot] = arr[end];
pivot = end;
//右边有坑,左边end找比key大的
while (begin < end && arr[begin] < key)
{
begin++;
}
//大的放到右边的坑里,左边begin自己形成新的坑
arr[pivot] = arr[begin];
pivot = begin;
}
//最后begin和end相遇了,把key放入该位置
pivot = begin;
arr[begin] = key;
}
1.4 整体排序
要利用分治递归思想。第一趟排序把整个数组分割成了左子序列和右子序列,如果左右子序列都有序了,那么整个数组就有序了,所以再递归使用前面的挖坑算法,再找出关键字,再把左右子序列分割成子序列…… 直到关键字的左右两边只有一个数据不可再递归,或者是关键字的左序列,右序列都是有序,那么整体就有序了。
如图所示:
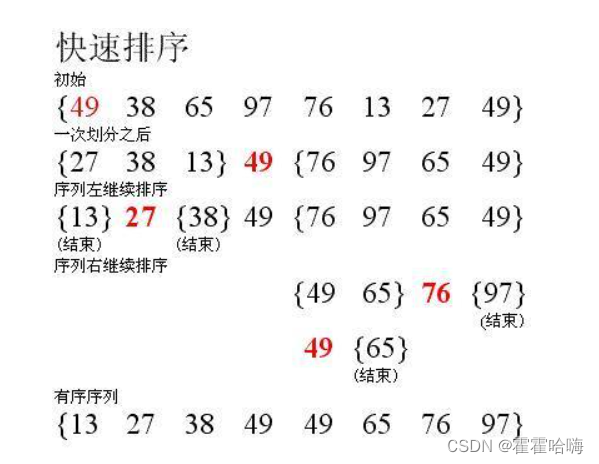
1.5 整体排序过程代码实现如下:
注意:因为是左右子序列,所以要控制一个区间。
void QuickySort(int* arr, int left,int right)
{
//当左右子区间不存在,或只有一个元素时,
//就不需要递归了,排序完成
if (left >= right)
{
return;
}
int begin = left;
int end = right;
int key = arr[begin];
int pivot = begin;
//这是排一趟,只排好了一个数
while (begin < end)
{
//左边有坑,右边end找比key小的
while (begin < end && arr[end] > key)
{
end--;
}
//小的放到了左边的坑里,右边end自己形成了新的坑
arr[pivot] = arr[end];
pivot = end;
//右边有坑,左边end找比key大的
while (begin < end && arr[begin] < key)
{
begin++;
}
//大的放到右边的坑里,左边begin自己形成新的坑
arr[pivot] = arr[begin];
pivot = begin;
}
//最后begin和end相遇了,把key放入该位置
pivot = begin;
arr[begin] = key;
//[left] pivot [right]
// [left pivot-1] pivot [pivot+1 right]
//左子区间和右子区间有序,整体就有序了
QuickySort(arr, left, pivot-1);
QuickySort(arr, pivot+1, right);
}
2. 快速排序的优化
2.1 三数取中
上文快排的算法思想有一个致命的缺陷:那就是当数据为有序时,其时间复杂度为O(N*N)。
原因:这是因为在取关键字 key 的值时,一直都是选最左边(或最右边)的数据。当数组本为升序时,每次关键字的右子序列的值都比它大,再次递归调用时,右子序列的子序列也是如此(降序同理)。
所以这个缺陷的原因就是 key 的取值。
那该如何取 key的值呢?一个比较好的方法是三数取中。
三数取中:并不是指取所有数据中间的那数,而是指在三个数中取那个不大不小的中间数,这个数可能在最左边,也可能在最右边。
通过这种类似随机选数的方法,就能保证一定不是数据中最大或最小的值做 key。
2.1.1 三数取中的代码的实现:
//三数取中
int GetMidIndex(int* arr, int left, int right)
{
//右移有除2的效果
int mid = (left + right) >> 1;
if (arr[mid] > arr[left])
{
if (arr[mid] < arr[right])
{
return mid;
}
else if(arr[left]>arr[right])
{
return left;
}
else
{
return right;
}
}
else //arr[mid] < arr[left]
{
if (arr[mid] > arr[right])
{
return mid;
}
else if (arr[left] < arr[right])
{
return left;
}
else
{
return right;
}
}
}
但是挖坑算法中我们习惯拿 begin 作为 key ,为了保持挖坑算法不被改变,我们把 begin 指向的值和通过三数取中选出的数的指向的值进行交换,确保 key 仍是begin指向的值。
代码实现为:
void Swap(int* p1, int* p2)
{
int tmp = *p1;
*p1 = *p2;
*p2 = tmp;
}
void QuickySort(int* arr, int left,int right)
{
//当左右子区间不存在,或只有一个元素时,
//就不需要递归了,排序完成
if (left >= right)
{
return;
}
int begin = left;
int end = right;
int index = GetMidIndex(arr, left, right);
Swap(&arr[index], &arr[left]);//交换一下,保证key还是最左边的数
int key = arr[begin];
int pivot = begin;
//这是排一趟,只排好了一个数
while (begin < end)
{
//左边有坑,右边end找比key小的
while (begin < end && arr[end] > key)
{
end--;
}
//小的放到了左边的坑里,右边end自己形成了新的坑
arr[pivot] = arr[end];
pivot = end;
//右边有坑,左边end找比key大的
while (begin < end && arr[begin] < key)
{
begin++;
}
//大的放到右边的坑里,左边begin自己形成新的坑
arr[pivot] = arr[begin];
pivot = begin;
}
//最后begin和end相遇了,把key放入该位置
pivot = begin;
arr[begin] = key;
// [left] pivot [right]
// [left pivot-1] pivot [pivot+1 right]
// 左子区间和右子区间有序,整体就有序了
QuickySort(arr, left, pivot-1);
QuickySort(arr, pivot+1, right);
}
2.2 小区间优化
我们知道在函数调用的过程中会在内存中建立栈帧,栈帧的建立也是需要时间和空间的。假设用上述代码排100W个数据,则大致有20层的递归调用,但是在最后几层中就大概调用了80多万次函数,它占用了栈帧的绝大多数空间和时间。
那么有人就会想,能不能把最后几层的函数递归调用消除呢?
官方给出的一种方法是小区间优化法,用于减少递归调用次数。
就是在排序的过程中当左右子序列中的数据个数大于某个数量时,不进行递归了,而是选用其他排序算法进行排序。这里一般用插入排序。
2.2.1 小区间优化的代码实现:
(注意:插入排序的算法这里没有给出,想要了解的请前往我的主页。)
//小区间优化法:减少递归调用次数
// keyindex - 1 - left 指子序列中的元素个数
// > 10是我们控制的一个界限
if (keyindex - 1 - left > 10)
{
QuickySort(arr, left, keyindex - 1);
}
else
{
// arr + left 是指这时的子序列不一定从第一个元素开始
//keyindex - 1 - left + 1 是指元素的个数
InsertSort(arr + left, keyindex - 1 - left + 1);
}
if (right - (keyindex + 1) > 10)
{
QuickySort(arr, keyindex + 1, right);
}
else
{
InsertSort(arr + keyindex + 1, right - (keyindex + 1) + 1);
}
但是由于小区间优化所带来的效率提升并不显著,而且它是与我们所控制的那个界限有关,所以平时并没有过于注重这个优化。
3.挖坑法的完整排序代码
void Swap(int* p1, int* p2)
{
int tmp = *p1;
*p1 = *p2;
*p2 = tmp;
}
//三数取中
int GetMidIndex(int* arr, int left, int right)
{
//右移有除2的效果
int mid = (left + right) >> 1;
if (arr[mid] > arr[left])
{
if (arr[mid] < arr[right])
{
return mid;
}
else if(arr[left]>arr[right])
{
return left;
}
else
{
return right;
}
}
else //arr[mid] < arr[left]
{
if (arr[mid] > arr[right])
{
return mid;
}
else if (arr[left] < arr[right])
{
return left;
}
else
{
return right;
}
}
}
//挖坑法
int PartSort1(int* arr, int left, int right)
{
int index = GetMidIndex(arr, left, right);
Swap(&arr[index], &arr[left]);//交换一下,保证key还是最左边的数
int begin = left;
int end = right;
int key = arr[begin];
int pivot = begin;
//这是排一趟,只排好了一个数
while (begin < end)
{
//左边有坑,右边end找比key小的
while (begin < end && arr[end] > key)
{
end--;
}
//小的放到了左边的坑里,右边end自己形成了新的坑
arr[pivot] = arr[end];
pivot = end;
//右边有坑,左边end找比key大的
while (begin < end && arr[begin] < key)
{
begin++;
}
//大的放到右边的坑里,左边begin自己形成新的坑
arr[pivot] = arr[begin];
pivot = begin;
}
//最后begin和end相遇了,把key放入该位置
pivot = begin;
arr[begin] = key;
return key;
}
void QuickySort(int* arr, int left,int right)
{
//当左右子区间不存在,或只有一个元素时,
//就不需要递归了,排序完成
if (left >= right)
{
return;
}
int keyindex = PartSort1(arr, left, right);
// [left] keyindex [right]
// [left keyindex -1] keyindex [keyindex +1 right]
// 左子区间和右子区间有序,整体就有序了
QuickySort(arr, left, keyindex - 1);
QuickySort(arr, keyindex + 1, right);
//或是
/*if (keyindex - 1 - left > 10)
{
QuickySort(arr, left, keyindex - 1);
}
else
{
// arr + left 是指这时的子序列不一定从第一个元素开始
//keyindex - 1 - left + 1 是指元素的个数
InsertSort(arr + left, keyindex - 1 - left + 1);
}
if (right - (keyindex + 1) > 10)
{
QuickySort(arr, keyindex + 1, right);
}
else
{
InsertSort(arr + keyindex + 1, right - (keyindex + 1) + 1);
}*/
排序结果为:
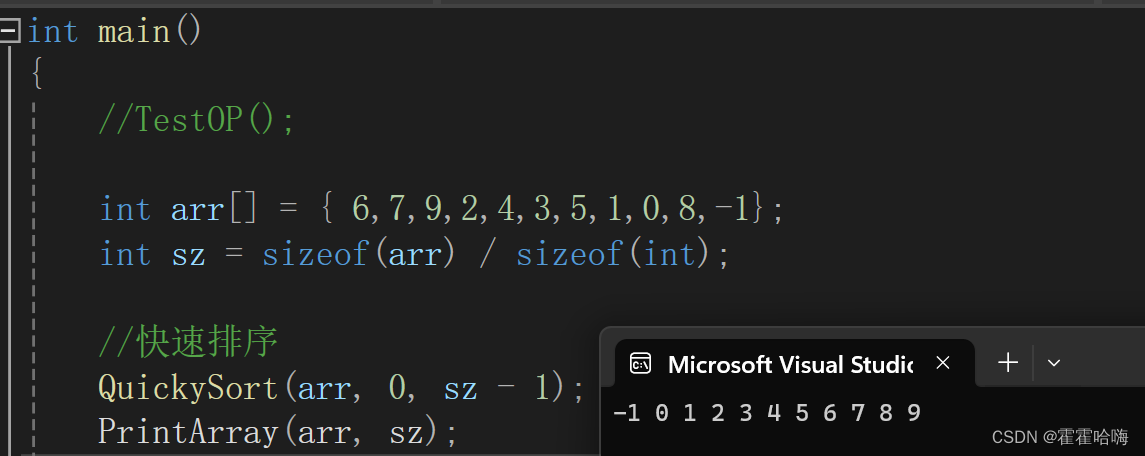
3.1 时间复杂度与稳定性
挖坑法的时间复杂度是O(N*logN),是不稳定的排序。
3. 左右"指针"法
3.1 算法思想:
与挖坑法类似,一般也要用三数取中法选一个关键字做 key,最终也是把整个数组分割成左右两个子序列,左子序列中所有元素均小于基准值,右子序列中所有元素均大于基准值。
只是实现的方式不同,左右"指针"法是分别从数组的最左边和最右边开始找数,左边的 begin 找比 key大的数,右边的 end 找比 key 小的数,找到后把这两个位置上的数交换,直到分割成左右两个子序列,然后左右子序列重复该过程,直到所有元素都排列在相应位置上为止。
3.2 单趟排序的图解如下:
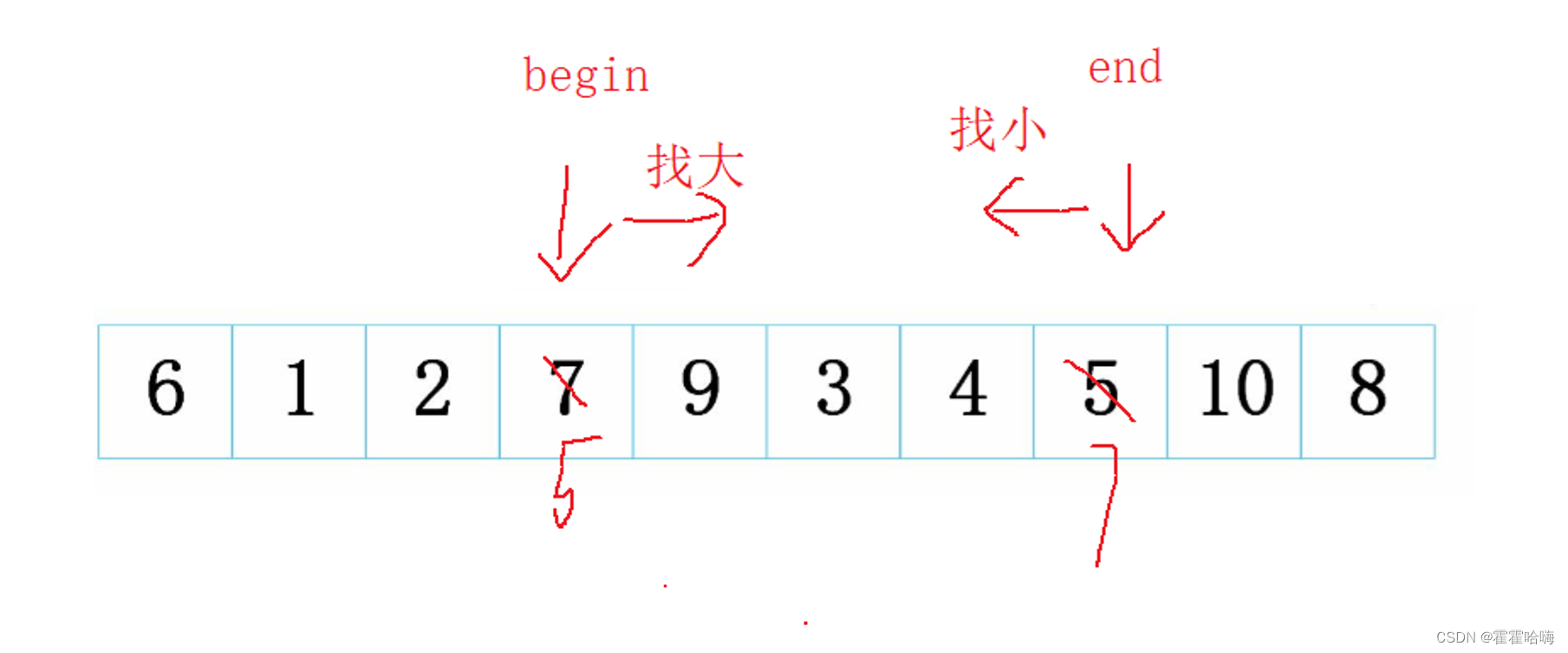
给定一无序数组,选第一个元素为关键字 keyi = 6,这里的keyi是数组的下标

begin++ 找比 keyi 大的数,end – 找比 keyi 小的数,找到后停下来交换
重复上述操作
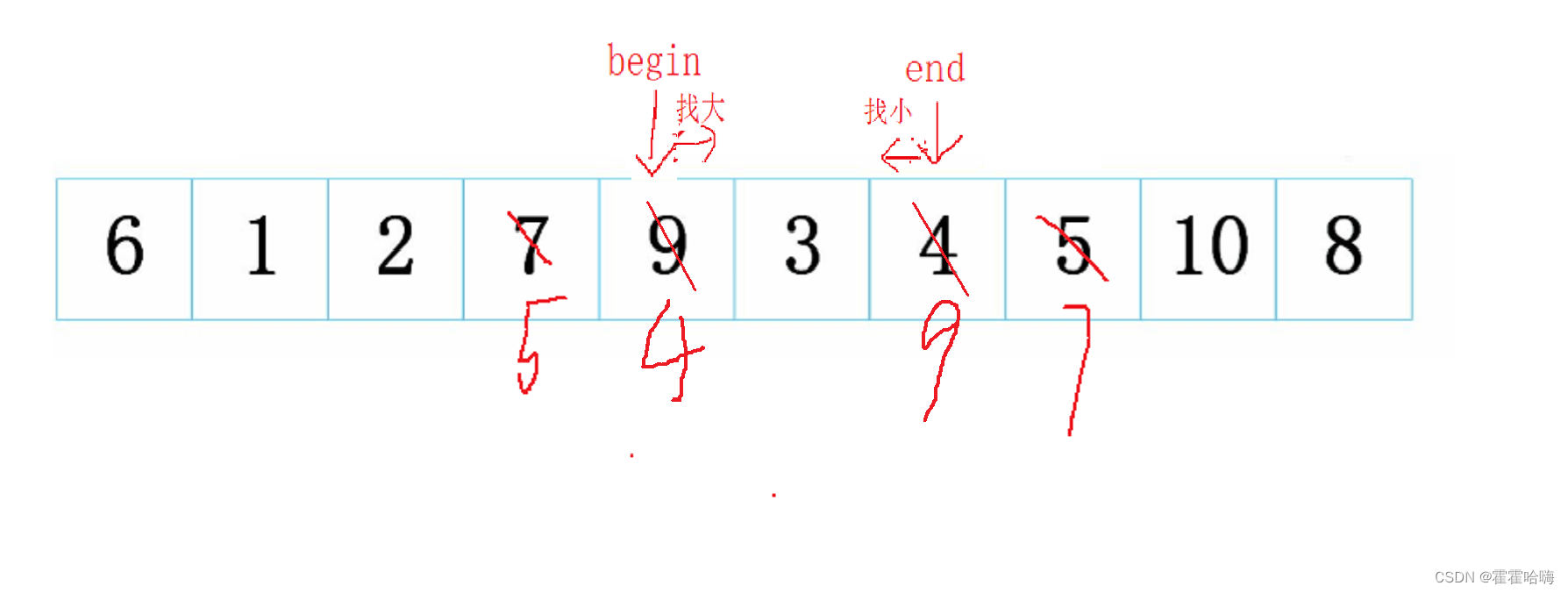
最后当 begin 和 end 相遇时,把相遇位置上的数与关键字 keyi所在位置的数 交换

最终排完第一趟后,以 keyi所指向的数6为基准,左边的元素都比它小,右边的元素都比它大。
3.3 单趟排序的代码实现:
注意:
1.代码中的三数取中函数与交换函数在上文,此处就直接调用
2.第二个和第三个while中的 begin < end 和 <= 中的等于号二者缺一不可。

//左右指针法
int PartSort2(int* arr, int left, int right)
{
int index = GetMidIndex(arr, left, right);
Swap(&arr[index], &arr[left]);//交换一下,保证key还是最左边的数
int begin = left;
int end = right;
int keyi = begin;//第一个元素的下标
while (begin < end)
{
//找比key小的
while (begin < end && arr[keyi] <= arr[end])
{
end--;
}
//找比key大的
while (begin < end && arr[keyi] >= arr[begin])
{
begin++;
}
Swap(&arr[begin], &arr[end]);
}
//当begin与end相遇时
Swap(&arr[begin], &arr[keyi]);
return begin;
}
4. 前后"指针"法
4.1 算法思想
与挖坑法类似,一般也要用三数取中法选一个关键字做 key,最终也是把整个数组分割成左右两个子序列,左子序列中所有元素均小于基准值,右子序列中所有元素均大于基准值。
只是实现方式不同,前后"指针"法是要定义两个前后变量( cur 和 prev,其中 cur 在前,prev 在后)分别指向数组的前两个元素,前面的 cur 先往前走,prev 后走,cur 找到比key 小的值,每次找到就停下来,prev++,再交换 prev 和 cur 所在位置的值。
直到分割成左右两个子序列,然后左右子序列重复该过程,直到所有元素都排列在相应位置上为止
4.2 单趟排序的部分图解如下:
给定一无序数组,选第一个元素为关键字 keyi = 6,这里的keyi是数组的下标
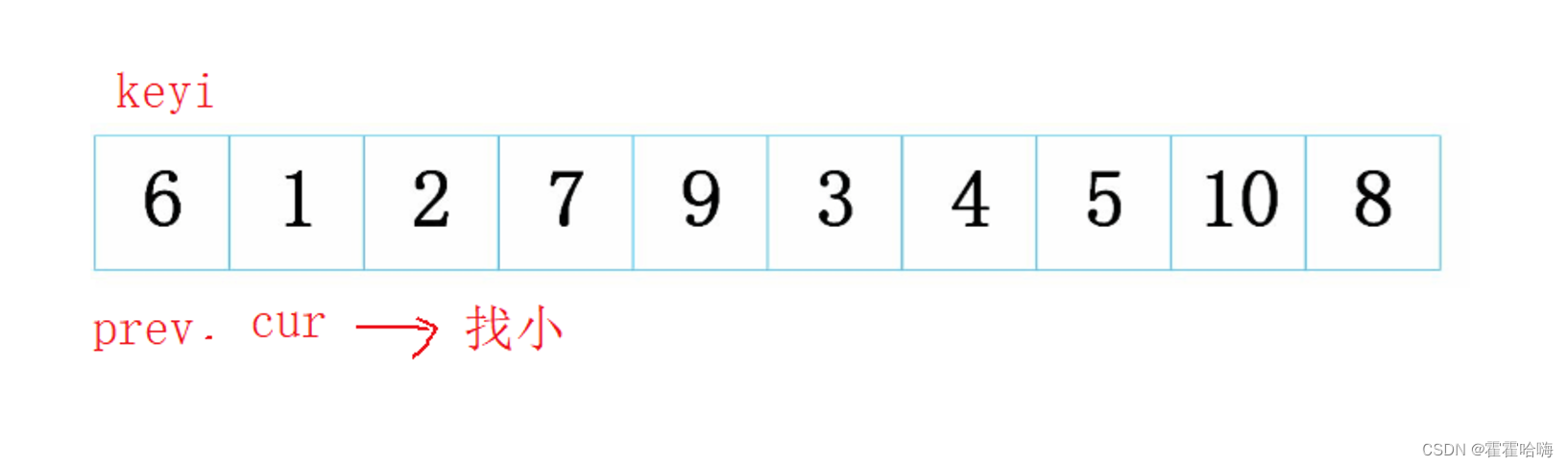
前几个数 cur 和 prev 重叠,省略图解
当cur在3的位置上时,prev指向7,此时,交换两数
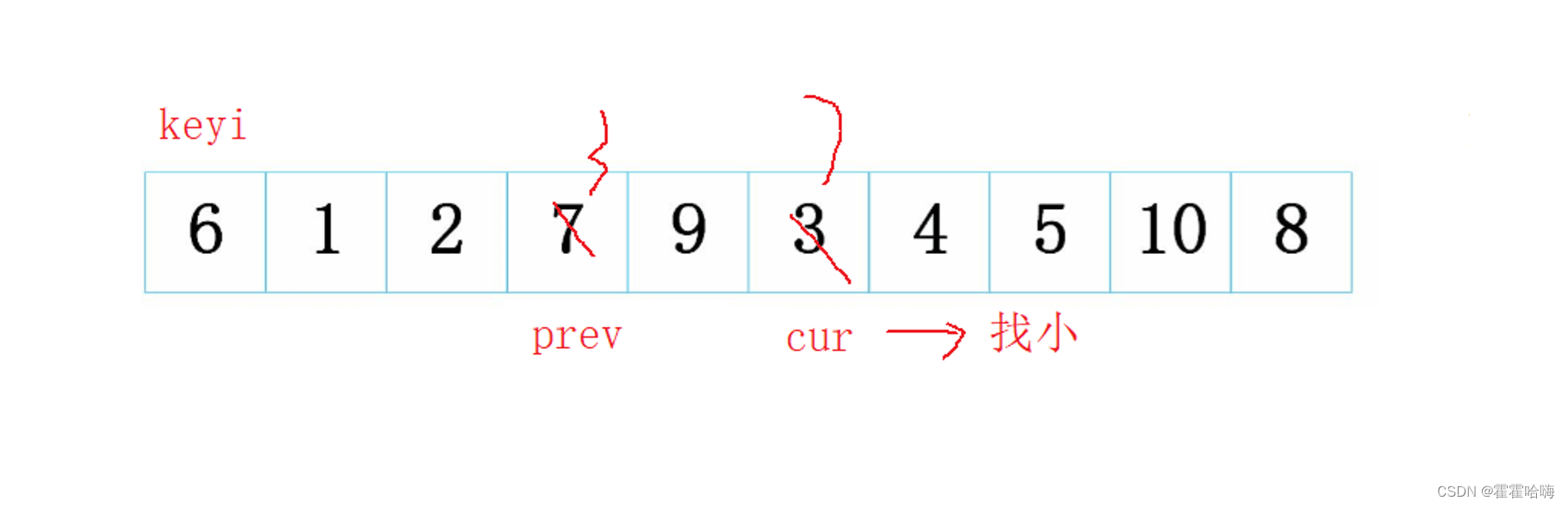
再cur++指向了4,停下,prev++指向了9,此时再交换
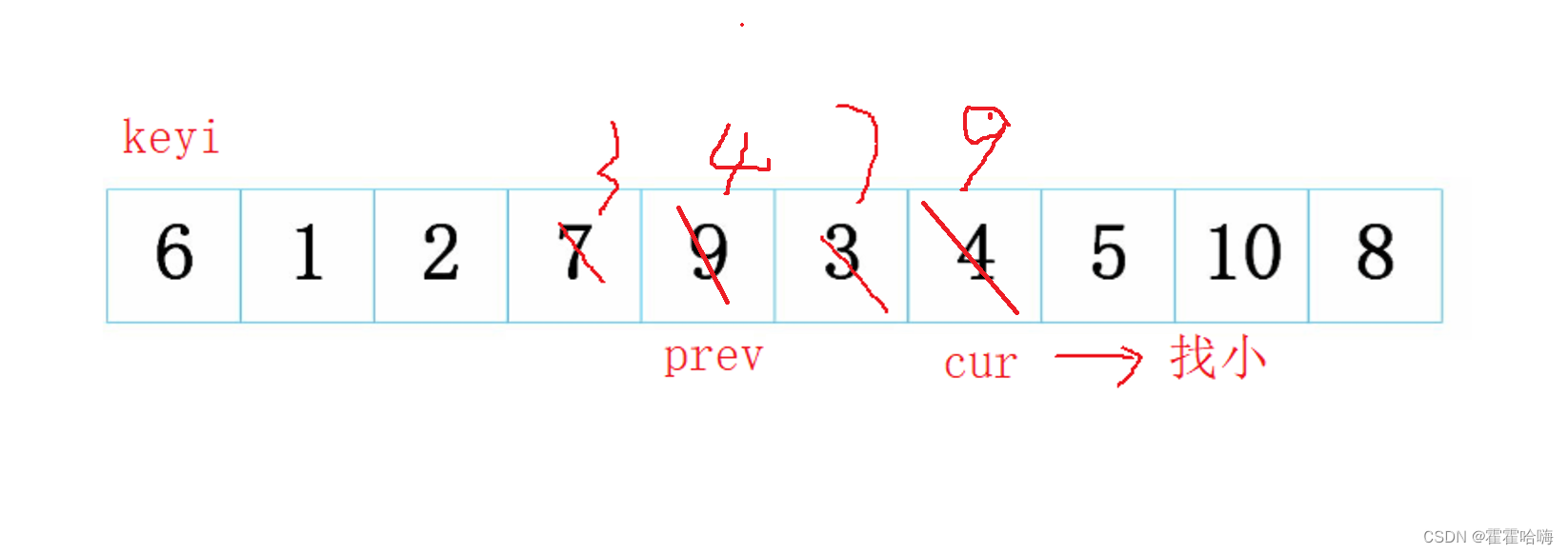
………………(重复上述操作)
当cur超出数组界限时,把此时 prev 所指向的值和 keyi 所指向的关键字交换,最终的结果是:
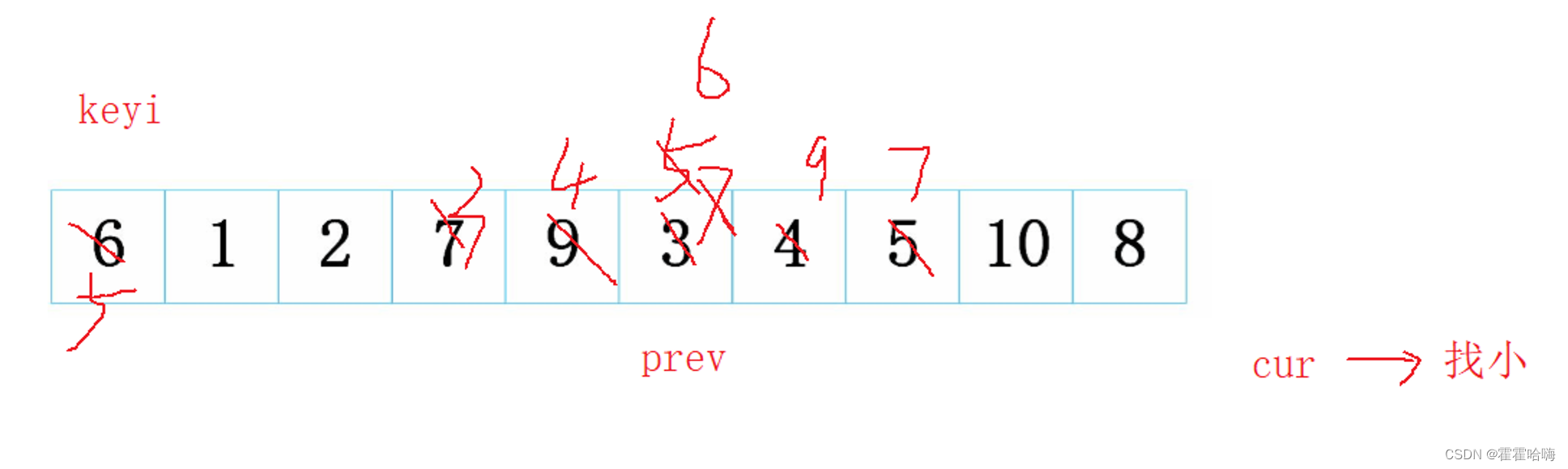
最终排完第一趟后,以 keyi所指向的数6为基准,左边的元素都比它小,右边的元素都比它大。
4.3 单趟排序的代码实现如下:
//前后指针法
int PartSort3(int* arr, int left, int right)
{
int index = GetMidIndex(arr, left, right);
Swap(&arr[index], &arr[left]);//交换一下,保证key还是最左边的数
int keyi = left;
int prev = left;
int cur = left + 1;
while (cur <= right)
{
if (arr[cur] < arr[keyi])
{
prev++;
Swap(&arr[cur], &arr[prev]);
}
cur++;
}
Swap(&arr[keyi], &arr[prev]);
return prev;
}
4.4 代码的小优化
通过上面的图解可知,当 cur 和 prev 重叠时,我们也进行了交换,但是这种自己和自己的交换其实是多于的。
优化代码如下:
在if判断条件中多了++prev != cur
int PartSort3(int* arr, int left, int right)
{
int index = GetMidIndex(arr, left, right);
Swap(&arr[index], &arr[left]);//交换一下,保证key还是最左边的数
int keyi = left;
int prev = left;
int cur = left + 1;
while (cur <= right)
{
//++prev != cur是指当cur和prev重合时不用多于的交换
if (arr[cur] < arr[keyi]&& ++prev != cur)
{
Swap(&arr[cur], &arr[prev]);
}
cur++;
}
Swap(&arr[keyi], &arr[prev]);
return prev;
}
二,快速排序总结:
- 快速排序的三种思想虽然实现方式不同,但是最终结果都是以key为基准值把整个数组分割成左右两个子序列,左子序列中所有元素均小于基准值,右子序列中所有元素均大于基准值。
- 在我们日常写快速排序算法时,那两种优化方式三数取中,最小区间优化并不是一定要有,可以根据情况自主添加。
1.比如没有优化的挖坑法的代码实现:
void QuickySort(int* arr, int left,int right)
{
//当左右子区间不存在,或只有一个元素时,
//就不需要递归了,排序完成
if (left >= right)
{
return;
}
int begin = left;
int end = right;
int key = arr[begin];
int pivot = begin;
//这是排一趟,只排好了一个数
while (begin < end)
{
//左边有坑,右边end找比key小的
while (begin < end && arr[end] > key)
{
end--;
}
//小的放到了左边的坑里,右边end自己形成了新的坑
arr[pivot] = arr[end];
pivot = end;
//右边有坑,左边end找比key大的
while (begin < end && arr[begin] < key)
{
begin++;
}
//大的放到右边的坑里,左边begin自己形成新的坑
arr[pivot] = arr[begin];
pivot = begin;
}
//最后begin和end相遇了,把key放入该位置
pivot = begin;
arr[begin] = key;
//[left] pivot [right]
// [left pivot-1] pivot [pivot+1 right]
//左子区间和右子区间有序,整体就有序了
QuickySort(arr, left, pivot-1);
QuickySort(arr, pivot+1, right);
}
void PrintArray(int* arr, int sz)
{
for (int i = 0; i < sz; i++)
{
printf("%d ", arr[i]);
}
printf("\n");
}
int main()
{
int arr[] = { 6,7,9,2,4,3,5,1,0,8,-1};
int sz = sizeof(arr) / sizeof(int);
//快速排序
QuickySort(arr, 0, sz - 1);
PrintArray(arr, sz);
}
2.比如没有优化的前后"指针"法的代码实现:
void Swap(int* p1, int* p2)
{
int tmp = *p1;
*p1 = *p2;
*p2 = tmp;
}
void QuickySort(int* arr, int left,int right)
{
//当左右子区间不存在,或只有一个元素时,
//就不需要递归了,排序完成
if (left >= right)
{
return;
}
int keyi = left;
int prev = left;
int cur = left + 1;
while (cur <= right)
{
//++prev != cur是指当cur和prev重合时不用多于的交换
if (arr[cur] < arr[keyi]&& ++prev != cur)
{
Swap(&arr[cur], &arr[prev]);
}
cur++;
}
Swap(&arr[keyi], &arr[prev]);
//[left] pivot [right]
// [left pivot-1] pivot [pivot+1 right]
//左子区间和右子区间有序,整体就有序了
QuickySort(arr, left, keyi-1);
QuickySort(arr, keyi+1, right);
}
void PrintArray(int* arr, int sz)
{
for (int i = 0; i < sz; i++)
{
printf("%d ", arr[i]);
}
printf("\n");
}
int main()
{
int arr[] = { 6,7,9,2,4,3,5,1,0,8,-1};
int sz = sizeof(arr) / sizeof(int);
//快速排序
QuickySort(arr, 0, sz - 1);
PrintArray(arr, sz);
}
三,冒泡排序
1.基本思想:
从序列的一端开始往另一端冒泡,依次比较相邻的两个数的大小。
设数组长度为N。
1.每轮比较相邻的前后两个数据,如果前面数据大于(或者小于)后面的数据,就将这两个个数据交换。
2.这样每轮对数组的第0个数据到N-1个数据进行一次遍历后,最大或者最小的一个数据就到数组第N-1个位置。
3.第一轮比较到下标为N-1的数据(最后一个),以后每次比较都-1。
2.图解冒泡排序:
以 [ 8,2,5,9,7 ] 这组数字来做示例:
从左往右依次冒泡,将小的往右移动(排降序)
第一轮冒泡:
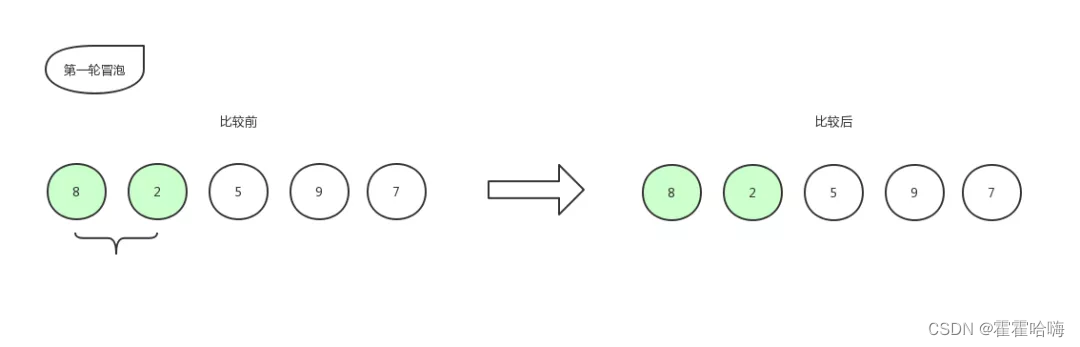
首先比较第一个数和第二个数的大小,我们发现 2 比 8 要小,那么保持原位,不做改动。位置还是 8,2,5,9,7 。指针往右移动一格,接着比较:
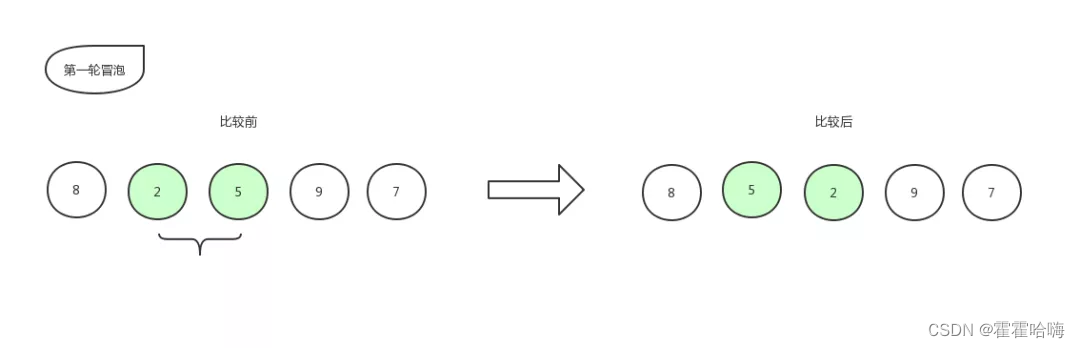
比较第二个数和第三个数的大小,发现 2 比 5 要小,所以位置交换,交换后数组更新为:[ 8,5,2,9,7 ]。
指针再往右移动一格,继续比较:
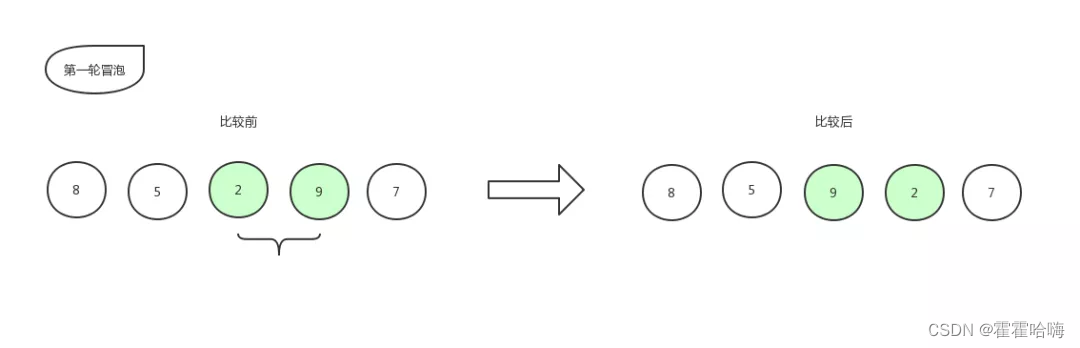
比较第三个数和第四个数的大小,发现 2 比 9 要小,所以位置交换,交换后数组更新为:[ 8,5,9,2,7 ]。同样,指针再往右移动,继续比较:
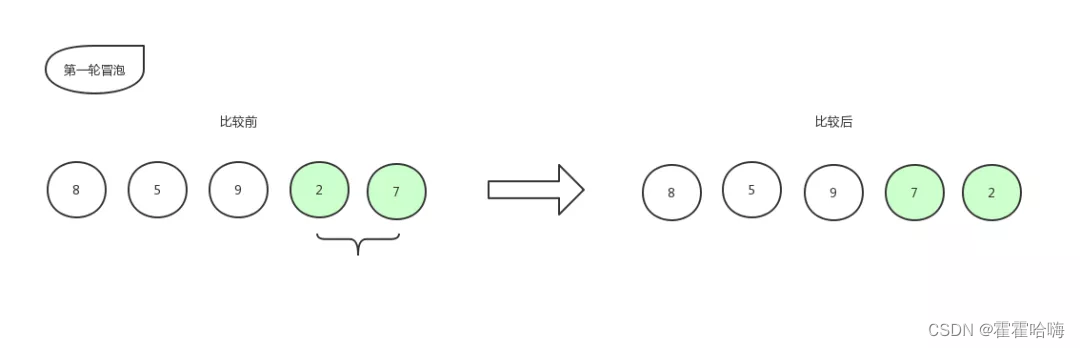
比较第 4 个数和第 5 个数的大小,发现 2 比 7 要小,所以位置交换,交换后数组更新为:[ 8,5,9,7,2 ]。
下一步,指针再往右移动,发现已经到底了,则本轮冒泡结束,处于最右边的 2 就是已经排好序的数字。
通过这一轮不断的对比交换,数组中最小的数字移动到了最右边。
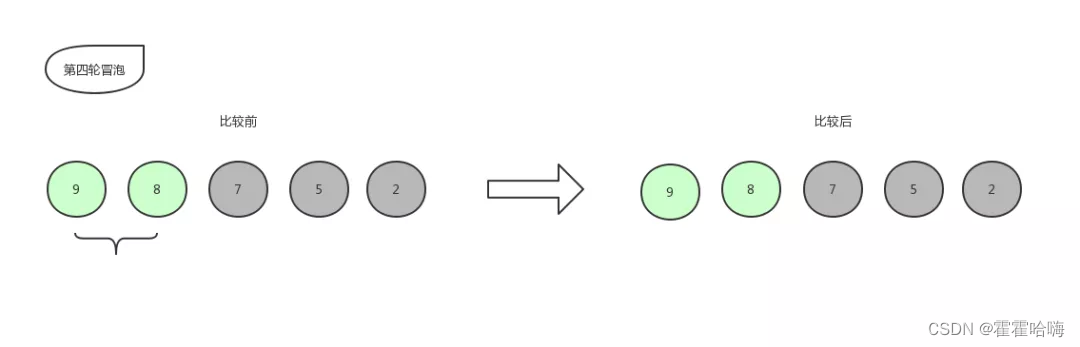
重复上述步骤,得到的最终结果是:
3.代码实现冒泡排序如下:
void Swap(int* p1, int* p2)
{
int tmp = *p1;
*p1 = *p2;
*p2 = tmp;
}
void BubbleSort(int* arr, int sz)
{
for (int j = 0; j < sz; j++)
{
//一趟排序
for (int i = 1; i < sz-j; i++)
{
if (arr[i - 1] < arr[i])
{
//前一个比后一个小,就交换
Swap(&arr[i - 1], &arr[i]);
}
}
}
}
4.冒泡排序的小优化:
假设我们要排降序,如果数组此时就是降序,那么在第一轮比较过后数据并没有发生交换,那就不要再进行多于的后续比较了,直接跳出循环即可。
void BubbleSort(int* arr, int sz)
{
for (int j = 0; j < sz; j++)
{
int exchange = 0;//默认是有序的
//一趟排序
for (int i = 1; i < sz-j; i++)
{
if (arr[i - 1] > arr[i])
{
//前一个比后一个大,就交换
Swap(&arr[i - 1], &arr[i]);
//如果不是有序的就发生了交换,exchange=1
exchange = 1;
}
}
//如果一趟比较过后发现是有序的,就直接跳出循环
if (exchange == 0)
{
break;
}
}
}
5.时间复杂度和稳定性的分析
最好:就是顺序时,时间复杂度为O(N)
乱序时:时间复杂度为O(N*N)
所以冒泡排序的时间复杂度是O(N*N)。
冒泡排序算法是稳定的。