算法思想-----数据结构

• 数据结构的存储方式 : 顺序存储(数组) , 链式存储(链表)

    顺序存储(数组) : 在内存中的存储空间是连续的 , 所以可以通过索引来获取存储的元素
    链式存储(链表) : 不是连续存储的 , 可能是这一个那一个的 .
    				 通常是由 数据域和指针域组成-->也就是data和next指针 (next指针指向下一个节点的地址)
  

• 数据结构底层逻辑

    所以啊 , 数据结构的那些东西(数组,链表,栈,队列,图,树,散列表等等)--->其实底层逻辑 都是数组或链表
  

• 数组和链表优缺点

  数组--->可以随机访问(通过索引) , 但是 需要考虑存储容量的问题
  链表--->没有存储容量的问题 , 但是不能随机访问元素
  

• 数据结构存在的意义

    数据结构存在的意义---->就是为了处理数据啊(增删改查)--->怎么增删改查呢?---->遍历+递归
    那为什么会有那么多种数据结构呢 ? ---->因为每种数据结构的应用场景不一样(灵活应用,优化代码嘛) 
  

动态规划(DP)

0.题目特点

• 1.计数（问：how many ways。。。）
  • a.有多少种方式 走到右下角
  • b.有多少种方法 选出k个数使得和是sum
• 2.求最大值、最小值（最大的一个解题类型）
  • a.从左上角走到右下角 路径的最大数字和
  • b.最长上升子序列的长度
• 3.求存在性
  • a.取石子游戏，先手是否必胜
  • b.能不能选出k个数 使得和是sum

1.【重点】经典例题(简单一维dp）

1.斐波那契数列

1 1 2 3 5 8 …

这是最经典的递归问题，
但 如果用递归求解，会重复计算一些子问题。
那如何用 动态规划 求解呢。

题目描述：求斐波那契数列的第n项，n<39。

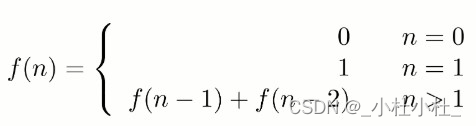
• 递归法
  根据递推公式：f(n) = f(n-1)+f(n-2)

int fib(int n){
	if(n<2) return n;
	return fib(n-1)+fib(n-2);
}

• dp
  • 1.状态 ： 最后一步是求f[n]
  • 2.转移方程：f[n] = f[n-1]+f[n-2]
  • 3.初始化：f[1]=1 ；边界条件：n<=1
  • 4.计算顺序：1—>n

public int Fibonacci(int n){
	if(n <= 1) return n;	//边界条件
	int[] fib = new int[n+1];
	fib[1] = 1;		//初始化
	fib[2] = 1;
	for(int i=2;i<=n;i++){	//计算顺序
		 fib[i] = fib[i-1] + fib[n-2];	//状态方程
	return fib[n];
}

2.矩形覆盖

题目描述：我们可以用2*1的小矩形横着或竖着去覆盖更大的矩形。请问用n个2*1的小矩形无重叠的覆盖一个2*n的大矩形，总共有多少种方法？

• 分析：dp[1] = 1 ; dp[2] = 2

    要覆盖2*n的大矩形，
    可以先覆盖一个2*1的矩形，再覆盖2*(n-1)的矩形；
    也可以先覆盖两个个2*2的矩形，再覆盖2*(n-2)的矩形。
    而覆盖2*(n-1)和2*(n-2) 可以看做是子问题，传递下去
  

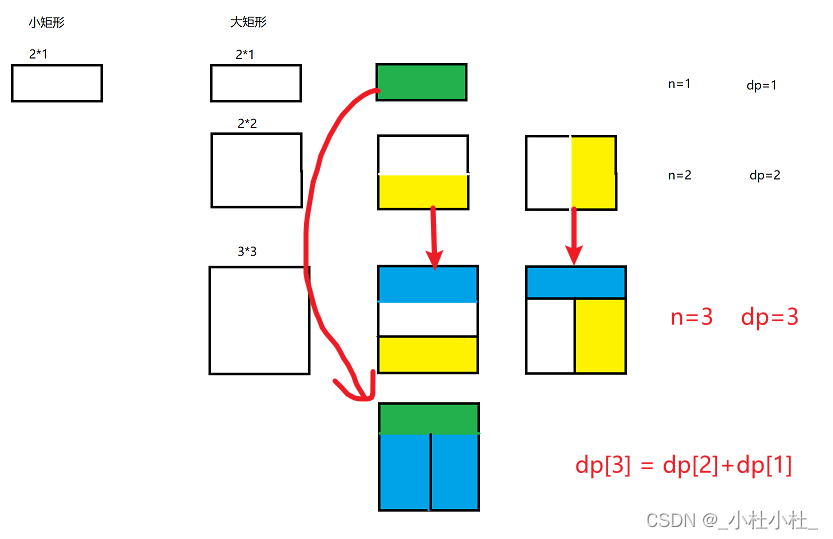
- 最后一步：求 dp[n]
- 初始化：dp[1] = 1 ; dp[2] = 2;  边界条件：n<=2
- 转移方程（递归表达式）：dp[n] = dp[n-1] + dp[n-2]
- 计算顺序：1-->n

• 递归法

public int rectCover(int n){
	if(n<=2) return n;
	return rectCover(n-1)+rectCover(n-2);
}

• dp算法

public int rectCover(int n){
	if(n<=2) return n;
	int[] dp = new int[n+1];
	dp[1] = 1;
	dp[2] = 2;
	for(int i=3;i<=n;i++){
		dp[i] = dp[i-1]+dp[i-2];
	}
	return dp[n];
}

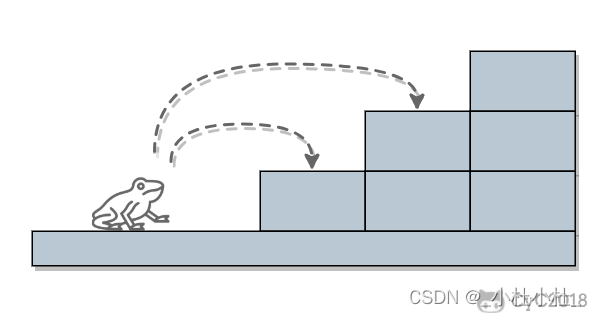
3.跳台阶

题目描述：一只青蛙一次可以跳上1级台阶，也可以跳上2级。求该青蛙跳上一个n级台阶总共有多少种跳法。

• 分析

    int[] dp = new int[n]; //dp[i]表示跳到第i级台阶有多少种跳法
    
    状态（最后一步）：d[n]
    初始化：dp[1] = 1 ; dp[2] = 1 ;
    边界条件：n<=2;
    状态转移方程：dp[i] = dp[i-1]+dp[i-2]; 	//dp[i]的状态，要么从i-1的台阶跳1级到i	； 要么从i-2级台阶一次跳2级到i
    计算顺序：1-->n 	//计算 dp[i] 需要先计算 dp[i-1] 和 dp[i-2]
  

public int jumpFloor(int n){
	if(n<=2) return n;
	int[] dp = new int[n+1];
	dp[1] = 1;
	dp[2] = 1;
	for(int i=3;i<=n;i++）{
		dp[i] = dp[i-1]+dp[i-2];
	}
	return dp[n];
}

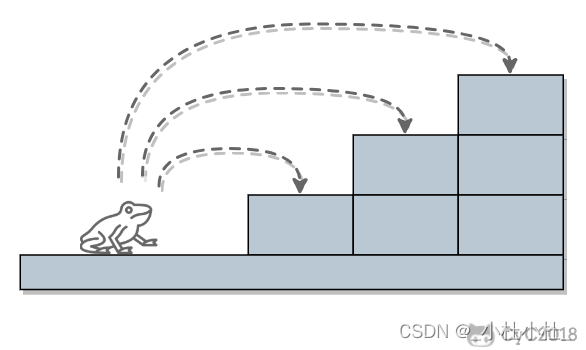
4.变态跳台阶

题目描述：一只青蛙可以跳上1级台阶，也可以跳上2级…它也可以跳上n级。求该青蛙跳上一个n级的台阶总共有多少种跳法。

• 分析

    最后一步：求 dp[n] //跳上n级台阶的方案数
    初始化：dp[1] = 1,dp[2] = 1,...,dp[n] = 1
    状态转移方程：dp[i] = dp[i-1]+dp[i-2]+...+dp[1]	//从所有台阶上都可以调到i级台阶上去
    计算顺序：1-->n
  

• 代码实现

public int jumpFloorII(int n){
	int[] dp = new int[n+1];
	Arrays.fill(dp,1);	//把dp数组中所有元素初始化为1
	//对于每一级台阶，方案数都是前面所有台阶的方案数的和
	for(int i=1;i<=n;i++){	
		for(int j=1;j<i;j++){
			dp[i] += dp[j];
		}
	}
	return dp[n];
}

2.我的日常练习汇总(DP)

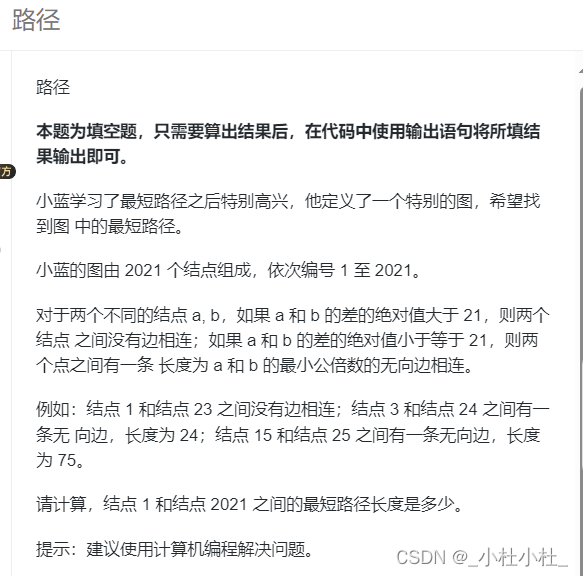
1.蓝桥真题-----路径

蓝桥真题:路径

import java.util.Arrays;
import java.util.Scanner;
// 1:无需package
// 2: 类名必须Main, 不可修改

public class Main {
    public static void main(String[] args) {
        Scanner scan = new Scanner(System.in);
        //在此输入您的代码...
        //最短路径-->dp
        //最小公倍数 = 两数乘积/最大公约数
        System.out.println(check());
        scan.close();
    }

    public static int check(){
      int[] dp = new int[2021+1];
      //结束条件 
      //初始化
      Arrays.fill(dp,Integer.MAX_VALUE);
      dp[1] = 0;
      dp[2] = 2;
      
      for(int i=3;i<=2021;i++){
        for(int x=i-21;x<i;x++){
          if(x<=0) continue;
          dp[i] = Math.min((dp[x] + lcm(i,x,gcb(i,x))) , dp[i]);
        }
      }
      return dp[2021];
    }

    public static int gcb(int a,int b){
      if(b == 0) return a;
      return gcb(b,a%b);
    }
    public static int lcm(int a,int b,int gcb){
      return (a*b)/gcb;
    }
}