欢迎来到博主的专栏C语言数据结构
博主ID：代码小豪

归并排序

两个有序数组的合并

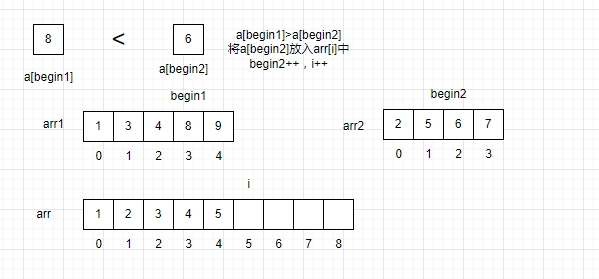
当前有两个有序数组arr1和arr2，我们创建一个可以容纳arr1和arr2同等元素个数的新数组arr。

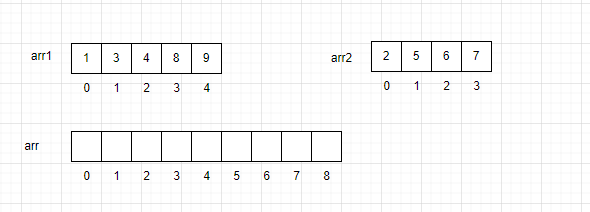
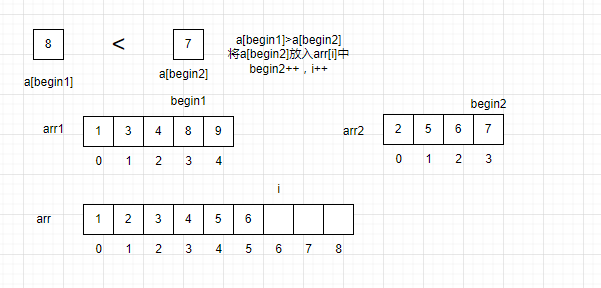
让一个指针指向arr1的队首，一个指针指向arr2的队首，还有一个指针指向arr的队首。依次对比两个数组之间的值的大小，将数据较小的值放入arr中，再将对应的指针指向下一个元素。

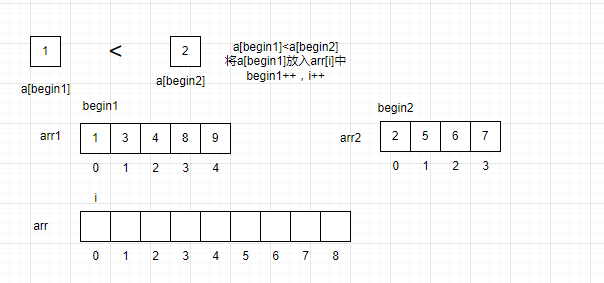
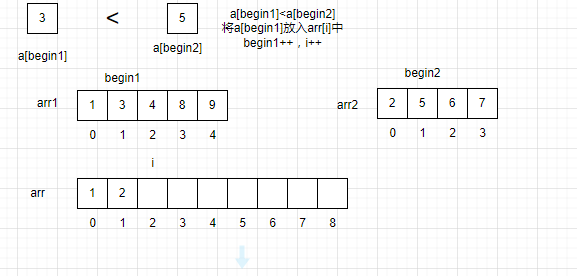
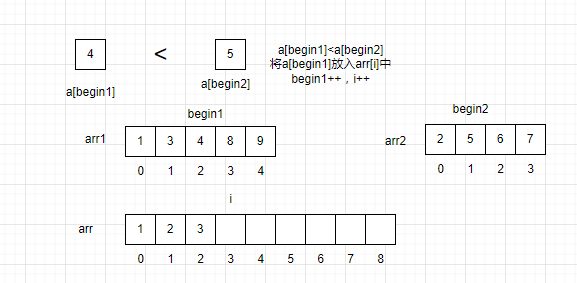
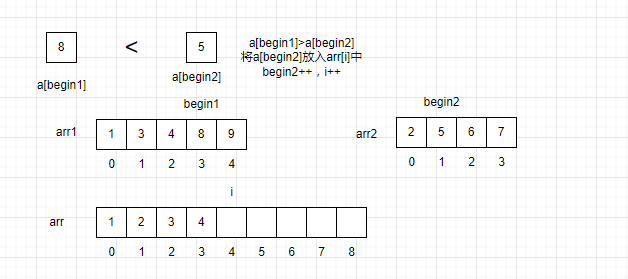
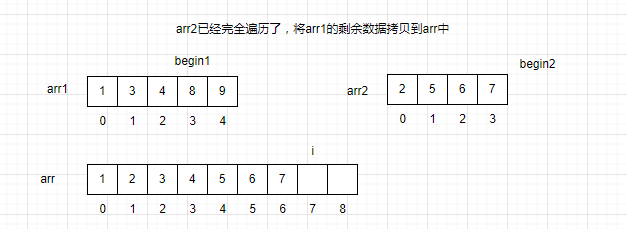
此时arr2已经遍历完了，将arr1的剩余数据全部拷贝到arr中。


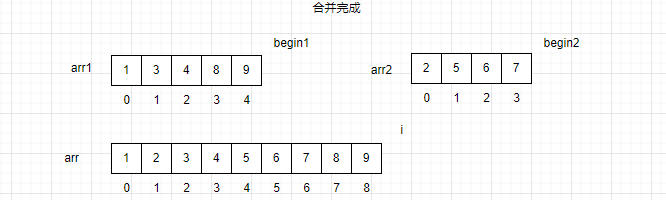
可以发现，这种方法将有序数组合并之后任然是一个有序的数组，这是否说明，我们可以利用数组合并的方式实现一种排序算法呢？

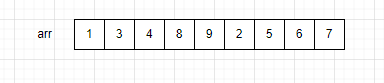
这是一个无序数组arr，但是将这个数组分为两半。

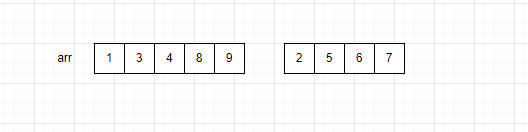
就可以将两部分合并成一个有序的数组。

但是绝大多数的无序数组都无法找到这个分界线，所以想要利用合并有序数组完成排序，就需要先将整体的数组分为两部分，其中一部分是有序数组，另外一部分也是有序数组，然后再将这两个有序数组合并，完成排序。

当数组中的元素个数越来越多，那么出现两个有序数组的概率就会越来越小，这是显而易见的现象，那么如果反过来想呢？若是数组中的数据只有两个，那么出现两个有序数组的概率是百分之百。

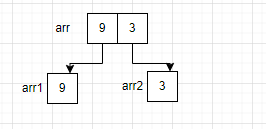
如果现在有四个元素组成的数组，那么由此法拆解后的子数组为：

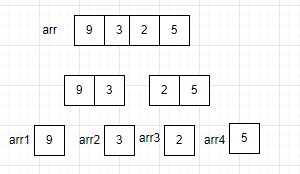
为什么要将一个数组分成N个大小为1的子序列呢？

可以发现，这些子序列都是有序的，那么将这些子序列进行有序合并，合并后的序列也就是有序的序列了。

归

相信大家再学高数的极限的时候都看过这么一句话：

一尺之捶，日取其半，万世不竭

意思就是将一个木棒，每天截取他的一半，永远都截不完。

当然数组是不会取不完的，如果将一个数组一直分成两半，最后就会得到一个元素组成的子序列。

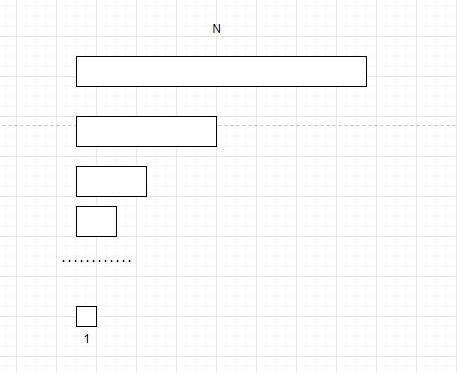
并

现在有N个元素为1的子序列，将两两相邻的子序列合并成有序序列。直到所有子序列构成一个数组为止

例如：

归并排序

将前3个操作联系起来就能实现归并排序。

归并排序的定义如下：

设初始序列含有n个记录，则可以看成是n个有序的子序列，每个子序列的长度为1，然后两两归并，得到n/2个长度为2或1的子序列，再两两合并……如此重复，直到得到一个长度为n的有序序列为止

归并排序的步骤如下：
（1）将整个数组二分递归，直到不可分为止（单数据序列）
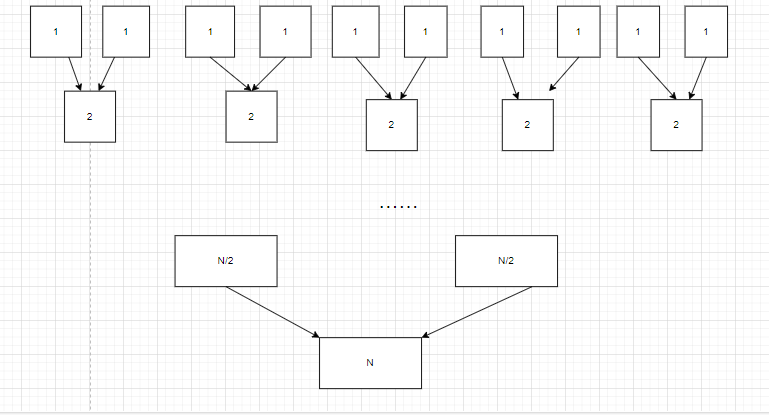
（2）由递归堆栈开始合并有序序列，最后将合并完成的数组拷贝到原数组。

这里讲讲合并数组时的递归堆栈，先通过递归将整个数组拆分。

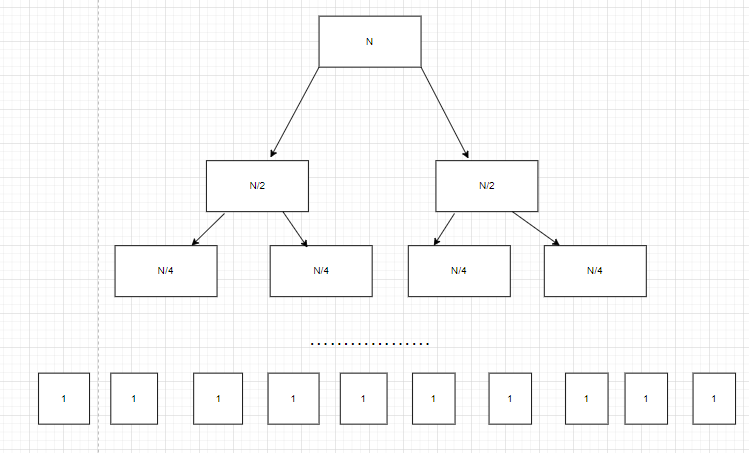
这个分解的方式与二叉树一致。完成分解之后就是将序列合并了。在调用堆栈的作用下，会将每个递归函数由下开始回溯。

归并排序的代码

void _MergeSort(int* a, int begin, int end,int* tmp)
{
	int mid = (begin + end) / 2;
	if (begin >= end)//不可再分，返回递归
	{
		return;
	}
	_MergeSort(a, begin, mid, tmp);
	_MergeSort(a, mid+1, end, tmp);


	int i = begin;

	//合并数组
	int begin1 = begin;//将原数组分为两部分，一部分是（begin，mid），另一部分是（mid+1，end）
	int end1 = mid;
	int begin2 = mid + 1;
	int end2 = end;

	while (begin1 <= end1 && begin2 <= end2)//合并有序数组
	{
		if (a[begin1] <= a[begin2])
		{
			tmp[i++] = a[begin1++];
		}
		else
		{
			tmp[i++] = a[begin2++];
		}
	}

	while (begin1 <= end1)//将剩余数据拷贝到临时数组
	{
		tmp[i++] = a[begin1++];
	}

	while (begin2 <= end2)//将剩余数据拷贝至临时数组
	{
		tmp[i++] = a[begin2++];
	}

	memmove(a+begin, tmp+begin, sizeof(int) * (end-begin + 1));//将合并的数组拷贝到原数组
}
void MergeSort(int* a, int n)
{
	int* tmp = (int*)malloc(sizeof(int) * n);//创建一个相等元素个数的数组、
	_MergeSort(a, 0, n - 1, tmp);
	free(tmp);
}