题目描述

已知一个长度为 n 的数组，预先按照升序排列，经由 1 到 n 次 旋转 后，得到输入数组。例如，原数组 nums = [0,1,2,4,5,6,7] 在变化后可能得到：

• 若旋转 4 次，则可以得到 [4,5,6,7,0,1,2]
• 若旋转 7 次，则可以得到 [0,1,2,4,5,6,7]

注意，数组 [a[0], a[1], a[2], ..., a[n-1]] 旋转一次 的结果为数组 [a[n-1], a[0], a[1], a[2], ..., a[n-2]] 。

给你一个元素值 互不相同 的数组 nums ，它原来是一个升序排列的数组，并按上述情形进行了多次旋转。请你找出并返回数组中的 最小元素 。

你必须设计一个时间复杂度为 O(log n) 的算法解决此问题。

样例输入

示例 1：

输入：nums = [3,4,5,1,2]
输出：1
解释：原数组为 [1,2,3,4,5] ，旋转 3 次得到输入数组。

示例 2：

输入：nums = [4,5,6,7,0,1,2]
输出：0
解释：原数组为 [0,1,2,4,5,6,7] ，旋转 3 次得到输入数组。

示例 3：

输入：nums = [11,13,15,17]
输出：11
解释：原数组为 [11,13,15,17] ，旋转 4 次得到输入数组。

提示：

• n == nums.length
• 1 <= n <= 5000
• -5000 <= nums[i] <= 5000
• nums 中的所有整数 互不相同
• nums 原来是一个升序排序的数组，并进行了 1 至 n 次旋转

题解

旋转排序数组的特点

在旋转排序数组中，nums[mid]的值与其两个端点值nums[0]和nums[nums.size()-1]有一定的关系。如图所示：

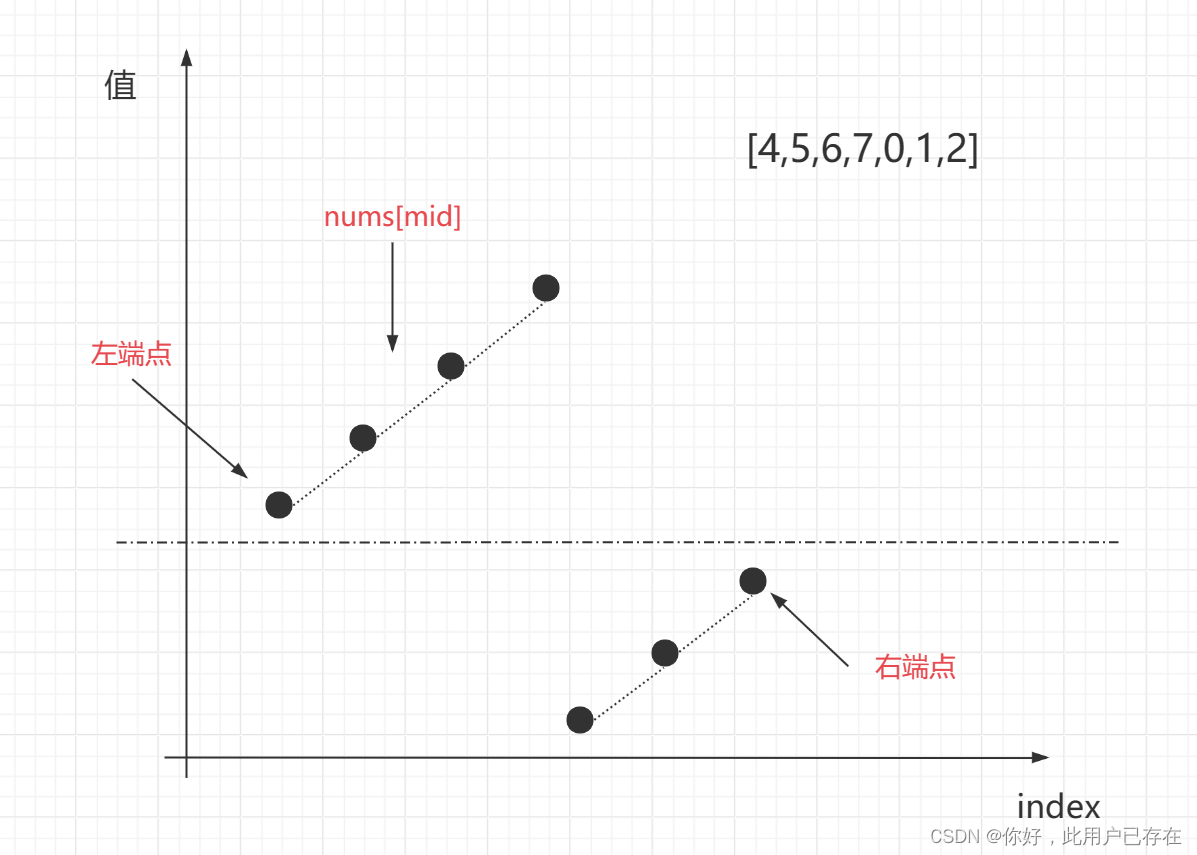
nums[mid]要么落入左侧区间，要么落入右侧区间，而判断nums[mid]落入哪个区间的条件就是和两个端点进行比较

• nums[mid]与nums[0]的关系：
  • nums[mid]>nums[0]，则nums[mid]落入左侧区间
  • nums[mid]<nums[0]，则nums[mid]落入右侧区间
• nums[mid]与nums[nums.size()-1]的关系
  • nums[mid]>nums[nums.size()-1]，则nums[mid]落入左侧区间
  • nums[mid]<nums[nums.size()-1]，则nums[mid]落入右侧区间

上述判定在具体题目中使用哪个以及如何使用可进一步根据题意分析，但是思想是重要的

为什么需要这个判定呢？

因为可以发现，无论nums[mid]落入左侧区间还是右侧区间，这两个区间之间不会发生重叠并且各自有序，因此我们可以根据nums[mid]落入哪个区间之后再进一步使用二分进行解题

在本题中，由于最小值在右侧区间，因此使用nums[mid]与nums[nums.size()-1]进行判定是比较容易的，因为可以避免两个区间中间端点带来的麻烦，代码如下所示

class Solution {
public:
    int findMin(vector<int>& nums) {
        int left=0,right=nums.size()-1;
        while(left<=right)
        {
            int mid=left+((right-left)>>1);
            if(nums[mid]>=nums[right])//nums[mid]在左侧区间，收缩左端点
            {
                left=mid+1;
            }else{//nums[mid]在右侧区间，收缩右端点
                right=mid;//不能使用right=mid-1，可能会在最后由于断点跳过结果值
            }
        }

        return nums[right];
    }
};