题目

---

有 N 个鱼塘排成一排，每个鱼塘中有一定数量的鱼，例如：N=5
时，如下表：

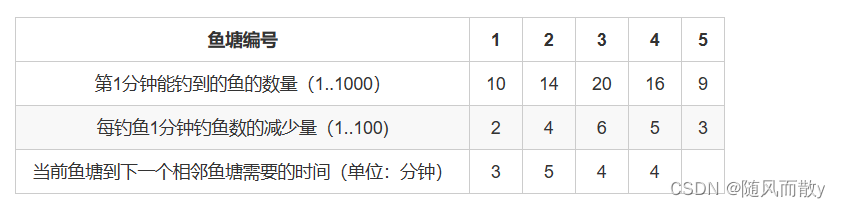
即：在第 1 个鱼塘中钓鱼第 1 分钟内可钓到 10 条鱼，第 2 分钟内只能钓到 8 条鱼，……，第 5 分钟以后再也钓不到鱼了。

从第 1 个鱼塘到第 2 个鱼塘需要 3 分钟，从第 2 个鱼塘到第 3 个鱼塘需要 5 分钟，……

给出一个截止时间 T，设计一个钓鱼方案，从第 1 个鱼塘出发，希望能钓到最多的鱼。

假设能钓到鱼的数量仅和已钓鱼的次数有关，且每次钓鱼的时间都是整数分钟。

---

输入

---

共 5 行，分别表示：
第 1 行为 N；
第 2行为第 1 分钟各个鱼塘能钓到的鱼的数量，每个数据之间用一空格隔开；
第 3 行为每过 1 分钟各个鱼塘钓鱼数的减少量，每个数据之间用一空格隔开；
第 4 行为当前鱼塘到下一个相邻鱼塘需要的时间；
第 5 行为截止时间 T。

---

输出

---

一个整数（不超过231−1），表示你的方案能钓到的最多的鱼。

---

样例

---

输入样例：
5
10 14 20 16 9
2 4 6 5 3
3 5 4 4
14

---

输出样例：
76

---

代码

#include<iostream>
#include<cstring>
using namespace std;
const int N = 110;
int n,t;
int a[N],d[N],l[N],spend[N];

int get(int i){
    return max(0,a[i]-d[i]*spend[i]);
}

int work(int n,int t){
    int res = 0;
    memset(spend,0,sizeof spend);
    for(int i=0;i<t;i++){
        int x=1;
        for(int j=2;j<=n;j++){
            if(get(x)<get(j)) x=j;
        }
        res += get(x);
        spend[x]++;
    }
    return res;
}

int main(){
    scanf("%d",&n);
    
    for(int i=1;i<=n;i++) scanf("%d",&a[i]);
    for(int i=1;i<=n;i++) scanf("%d",&d[i]);
    for(int i=2;i<=n;i++) scanf("%d",&l[i]),l[i]+=l[i-1];
    scanf("%d",&t);
    
    int res = 0;
    for(int i=1;i<=n;i++){
        res = max(res,work(i,t-l[i]));
    }
    
    printf("%d",res);
}