#上一章我们把搜索二叉树的知识给传授完毕，如果认真的看下去并且手打了几遍，基本上内部的逻辑还是可以理解的，那我们现在就截至继续学习树的一些重要知识啦~~

树高怎么求呀？如果用上一次学的层次遍历来求树高，有点小题大做了，这章我们就教大家如何用递归来求树高。

如何查找树里的元素呢？？

哈夫曼树是个啥子？？

在这一章节我都会很细致的给大家说明啦~

树高咋求？？？

🤔我们现在掌握的方法只有层次遍历来求树高，那我们怎么用递归来求树高呢？？？

我们现在先拿最极端情况来说明，如果一棵树没有一个元素，那我们的树高是不是为0，这样来看，我们的终止条件就找到啦！，没错就是当根节点为空的是后，我们就返回0；

我们的树高应该看最长的一部分，那我们就应该先定义两个高度，一个是左子树高度，另一个是右子树高度，之后我们比较左子树高度和右子树高度哪个高，哪个高哪个就决定了树高，因为左子树和右子树都是从第二层开始才有的，所以我们最后返回的树高应该让左右子树+1。

这样来看我们大概的逻辑不就出来了嘛？

先写一个极端判断条件，然后比较左右子树高度即可。

int treeheight(treenode* root)
{
	if(root==NULL)return 0;
	int lh=treeheight(root->lchild);
	int rh=treeheight(root->rchild);
	return lh>rh?lh+1:rh+1; 
}

这样看来是不是还挺简单嘞，嘿嘿。

那我们接着来下面的知识，如何查找元素嘞？

怎么查找树里面的元素？？？

查找的话，我们大概想一下就知道要用bool函数来判断啦，在这个结构中，我们首先要把根节点和查找的元素定义起来。

我们怎么查找呢？肯定也是一层一层查找，如果一棵树都查完了也没找的这个元素，那我们就可以说这棵树没有这个元素。

由此我们可以得到我们判断结束的条件，当树不为空时候，我们就循环；如果为空，我们就结束判断。

代码部分也是很简单，如下：
 

bool find(treenode* root,int target)
{
	while(root)
	{
		if(root->value==target)
		return 1;
		if(root->value<target)
		root=root->lchild;
		if(root->value>target)
		root=root->rchild;
	}
}

由以上内容，和之前的文章，我们现在掌握了如何构建查找二叉树，如何前中后序遍历，如何层次遍历，如何求树高，如何查找元素，二叉树中基本的知识，我们大概已经学完啦，下面我们来认识一个重要的树，哈夫曼树。

哈夫曼树

定义：

我们首先了解哈夫曼树的定义：

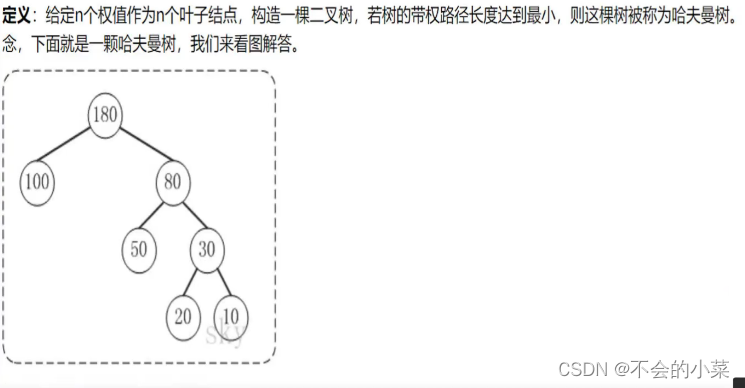
对于哈夫曼树，我们的权值只有叶子结点！！

性质：

1.权值越大的叶子节点越靠近根节点

2.权值越小的叶子节点越远离根节点

3.哈夫曼树并不唯一

4.哈夫曼树的子树也是哈夫曼树

5.哈夫曼树无度为1的结点

这些性质也是比较好看出来的，在这里就不多余赘述啦~

哈夫曼树的构建：

结点的不同：

在我们构建搜索二叉树时候，我们初始将左右子树设置为空，但是在我们的哈夫曼树的初始化时，我们应该将左右子树保留。

如下：

struct treenode{
	int weight;
	treenode* lchild;
	treenode* rchild;
	treenode(int v,treenode* l,treenode* r){
		weight=v,lchild=l,rchild=r;
	}
};

因为我们左右孩子会构造出来我们的根节点，所以左右孩子这里不为空。

构建过程：

1.我们首先要把每个节点初始化，之后push进我们的vector里面

2.定义左孩子，右孩子，根节点三个变量

3.对元素进行降序排列，之后再弹出最后两个元素，同时利用最后两个元素构建出我们的父节点。

（此时的父节点需要new来开辟空间）。

过程也相对容易，接下来是代码部分：

void build(vector<int> a){
	vector<treenode*>b;
	for(int i=0;i<a.size();i++)
	{
		treenode* tmp=new treenode(a[i],NULL,NULL);
		b.push_back(tmp);
	}
	treenode* l=NULL,*r=NULL,*p=NULL;
	while(b.size()>1){
		sort(b.begin(),b.end(),[=](treenode* a,treendoe* b){
			return a->weight>b.weight;
		});
		l=b[b.size()-1];b.pop_back();
		r=b[b.size()-1];b.pop_back();
		p=new treenode(l->weight+r->weight,l,r);
	}
	return p;
}

求WPL

怎么求wpl呢？这里就用到了我们之前学的层次遍历啦。

我们首先层次遍历，判断结点是否没有左右孩子，这样就能找到我们的叶子节点，然后乘以我们的层次-1，如此加和进去就可以得到我们的wpl啦

void layersearch(treenode* root)
{
	queue<treenode*>q;
	q.push(root);
	treenode* last=root;
	treenode* nlast=NULL;
	while(!q.empty()){
		treenode* tmp=q.front();
		cout<<tmp->weight;
		if(tmp->lchild==NULL&&tmp->rchild==NULL)
		{
			wpl+=tmp->weight*L;
		}
		q.pop();
		if(tmp->lchild==NULL)
		{
			q.push(tmp->lchild);
			nlast=tmp->lchild;
		}
		if(tmp->rchild==NULL)
		{
			q.push(tmp->rchild);
			nlast=tmp->rchild;
		}
		if(tmp==last)
		{
			cout<<endl;
			L++;
			last=nlast;
		}
	}
	
}

//以上就是我们树里面残留的问题啦，一些基本的原理和代码部分我都有提到，在这里还得看大家自己下去的实践能力，多打代码，才能更透彻的了解，理解底层逻辑。

如果我的文章对对大家有帮助的作用，希望大家多多支持哦~~（谢谢大家的点赞关注啦~）

阿里嘎多everybody~