【编译原理】手工打造语法分析器

news2024/11/17 12:33:53

重点：

语法分析的原理
递归下降算法（Recursive Descent Parsing）
上下文无关文法（Context-free Grammar，CFG）

关键点：

左递归问题
深度遍历求值 - 后续遍历

上一篇「词法分析器」将字符串拆分为了一个一个的 token。
本篇我们将 token 变成语法树。

一、递归下降算法

还是这个例子 int age = 45
我们给出这个语法的规则：

intDeclaration : Int Identifier ('=' additiveExpression)?;

如果翻译为程序的话，伪代码如下

// 伪代码
MatchIntDeclare(){
  MatchToken(Int)；        // 匹配 Int 关键字
  MatchIdentifier();       // 匹配标识符
  MatchToken(equal);       // 匹配等号
  MatchExpression();       // 匹配表达式
}

输出的 AST 类似于：

Programm Calculator
    IntDeclaration age
        AssignmentExp =
            IntLiteral 45

上面的过程，称为「递归下降算法」。
从顶部开始不断向下生成节点，其中还会有递归调用的部分。

二、上下文无关文法

上面的例子比较简单，还可以用正则表达式文法来表示。
但如果是个算数表达式呢？正则文法就很难表示了。

2+3*5
2*3+5
2*3

这时我们可以用递归的规则来表示

additiveExpression
    :   multiplicativeExpression
    |   additiveExpression Plus multiplicativeExpression
    ;
 
multiplicativeExpression
    :   IntLiteral
    |   multiplicativeExpression Star IntLiteral
    ;

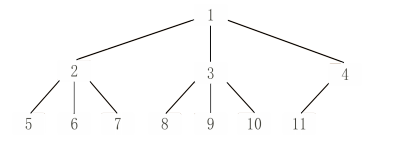
生成的 AST 为：

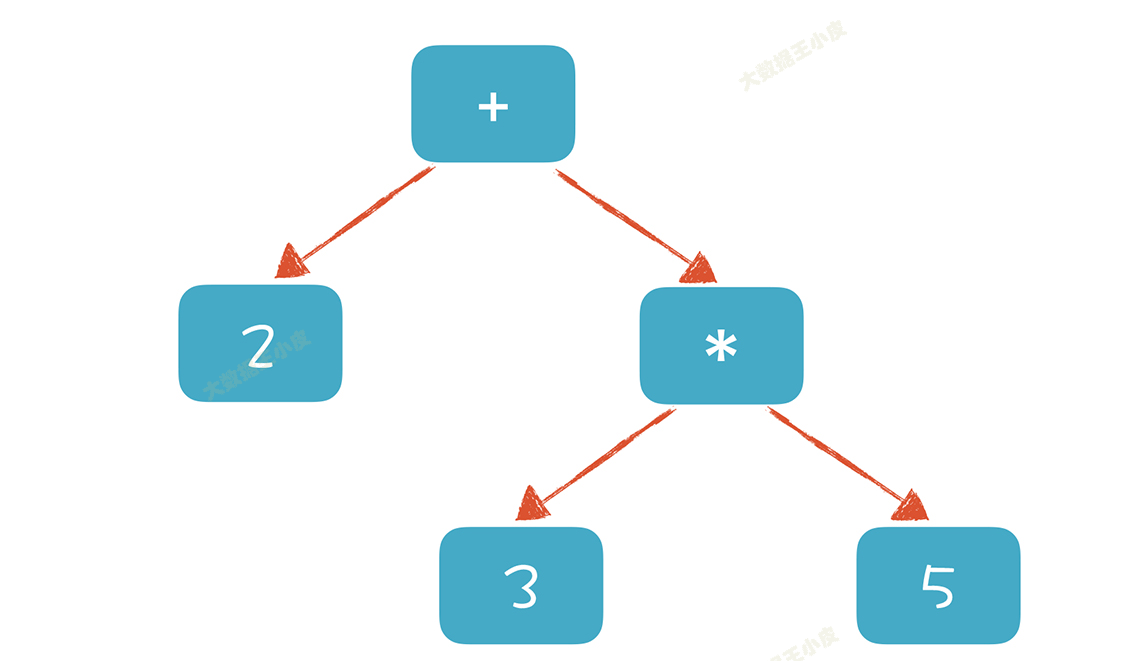
如果要计算表达式的值，只需要对根节点求值就可以了。
这个就叫做**「上下文无关文法」**。

但你把上述规则翻译为代码逻辑时，会发现一个问题，无限递归。
我们先用个最简单的示例：

	additiveExpression
    :   IntLiteral
    |   additiveExpression Plus IntLiteral
    ;

比如输入 2+3：

先判断其是不是 IntLiteral，发现不是
然后匹配 additiveExpression Plus IntLiteral，此时还没有消耗任何的 token
先进入的是 additiveExpression，此时要处理的表达式还是 2+3
又回到开始，无限循环

这里要注意的一个问题：
并不是觉得 2+3 符合 additiveExpression Plus IntLiteral 就能直接按照 + 拆分为两部分，然后两部分分别去匹配。
这里是顺序匹配的，直到匹配到该语法规则的结束符为止。
在 additiveExpression Plus IntLiteral 中 additiveExpression 的部分，也是在处理完整的 token 的（2+3）。

三、左递归解决方案

改为右递归

如何处理这个左递归问题呢？
我们可以把表达式换个位置：

	additiveExpression
    :   IntLiteral
    |   IntLiteral Plus additiveExpression
    ;

先匹配 IntLiteral 这样就能消耗掉一个 token，就不会无限循环了。
比如还是 2+3

2+3 不是 IntLiteral，跳到下面
2+3 的第一个字符是 2 被 IntLiteral 消耗掉，并结束 IntLiteral 匹配
然后 + 被 Plus 消耗掉
最后 3 进入 additiveExpression，匹配为第一条规则 IntLiteral

这样就结束了，没有无限循环。
改写成算法是：

private SimpleASTNode additive(TokenReader tokens) throws Exception {
    SimpleASTNode child1 = IntLiteral();  // 计算第一个子节点
    SimpleASTNode node = child1;  // 如果没有第二个子节点，就返回这个
    Token token = tokens.peek();
    if (child1 != null && token != null) {
        if (token.getType() == TokenType.Plus) {
            token = tokens.read();
            SimpleASTNode child2 = additive(); // 递归地解析第二个节点
            if (child2 != null) {
                node = new SimpleASTNode(ASTNodeType.AdditiveExp, token.getText());
                node.addChild(child1);
                node.addChild(child2);
            } else {
                throw new Exception("invalid additive expression, expecting the right part.");
            }
        }
    }
    return node;
}

但也有问题：
比如 2+3+4，你会发现它的计算顺序变为了 2+(3+4) 后面 3+4 作为一个 additiveExpression 先被计算，然后才会和前面的 2 相加。改变了计算顺序。

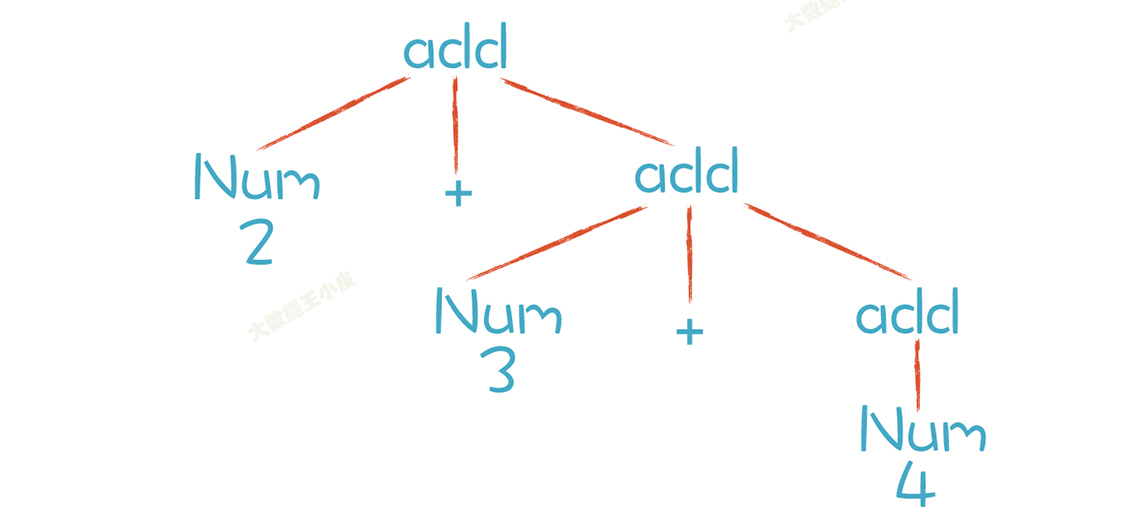
消除左递归

上面右递归解决了无限递归的问题，但是又有了结合优先级的问题。
那么我们再改写一下左递归：

additiveExpression
  :   IntLiteral additiveExpression'
  ;

additiveExpression'
  :		'+' IntLiteral additiveExpression'
  | 	ε
  ;

文法中，ε（读作 epsilon）是空集的意思。
语法树 AST 就变成了下图左边的样子，虽然没有无限递归，但是按照前面思路，使用递归下降算法，结合性还是不对。
我们期望的应该是右边的 AST 树样子。那么怎么才能变成右边的样子呢？

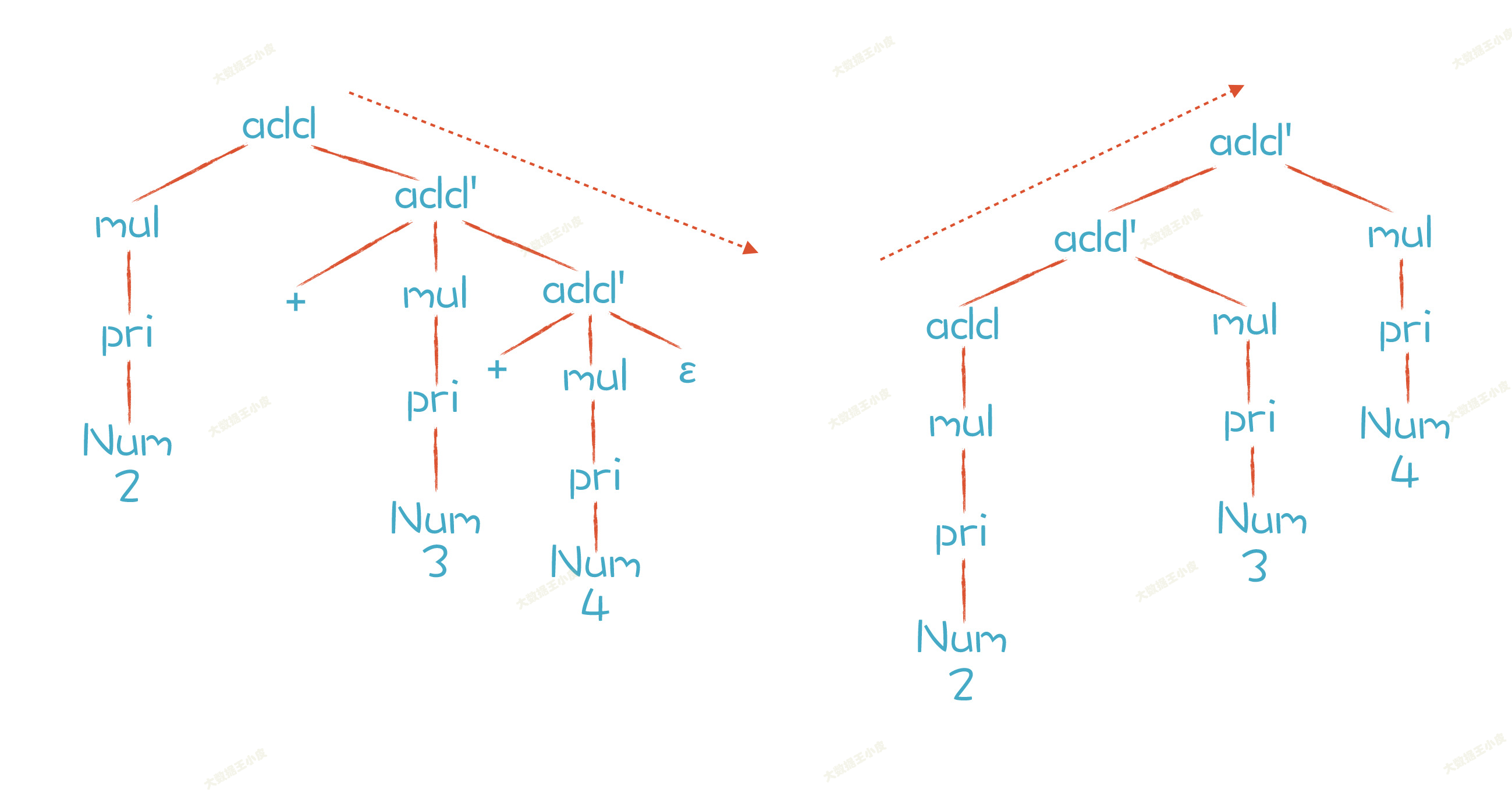
这里我们插入一个知识点：
前面语法规则的表示方式成为：「巴科斯范式」，简称 BNF
我们把下面用正则表达式简化表达的方式，称为「扩展巴科斯范式 (EBNF)」
add -> mul (+ mul)*

那么我们把上面的表达式改写成 EBNF 形式，变为：

additiveExpression -> IntLiteral ('+' IntLiteral)*

这里写法的变化，就能让我们的算法逻辑产生巨大的变化。

重点：
前面左递归也好、右递归也好，变来变去都是递归调用，导致无限循环、结合性的问题。如果我们干掉递归，用循环来代替，就能按照我们期待的方式来执行了。
这里的区别是：前面递归计算过程是后序，把最后访问到的节点先计算，然后再一步步的返回；而循环迭代是前序，先计算再往后访问。

我们再写出计算逻辑：

private SimpleASTNode additive(TokenReader tokens) throws Exception {
    SimpleASTNode child1 = IntLiteral(tokens);  // 应用 add 规则
    SimpleASTNode node = child1;
    if (child1 != null) {
        while (true) {                              // 循环应用 add'
            Token token = tokens.peek();
            if (token != null && (token.getType() == TokenType.Plus)) {
                token = tokens.read();              // 读出加号
                SimpleASTNode child2 = IntLiteral(tokens);  // 计算下级节点
                node = new SimpleASTNode(ASTNodeType.Additive, token.getText());
                node.addChild(child1);              // 注意，新节点在顶层，保证正确的结合性
                node.addChild(child2);
                child1 = node;
            } else {
                break;
            }
        }
    }
    return node;
}

消除了递归，只有循环迭代。你可以和上面递归的代码对比下。

再提一个概念：「尾递归」
尾递归就是函数的最后一句是递归的调用自身，可以理解为先序。而这种尾递归通常都可以转化为一个循环语句。

四、执行代码

前面我们已经把一个语句转换为了一个 AST 树，接下来我们遍历这个语法树，就能实现计算求值了。
以 2+3+4 为例，简化后的语法树长这样：

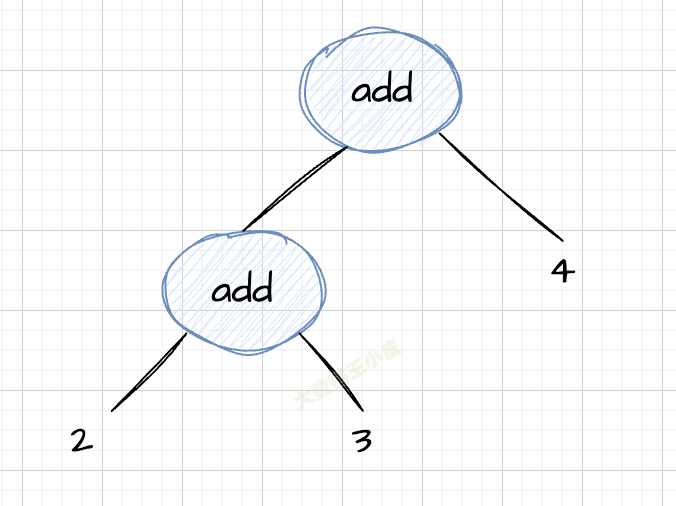
遍历的伪代码如下：

evaluate(node) {
    if node.type == TYPE.ADD:
        left_res = evaluate(node.getChild(0))
        right_res = evaluate(node.getChild(1))
        return left_res + right_res
    else if node.type == TYPE.INT:
        return node.val
}