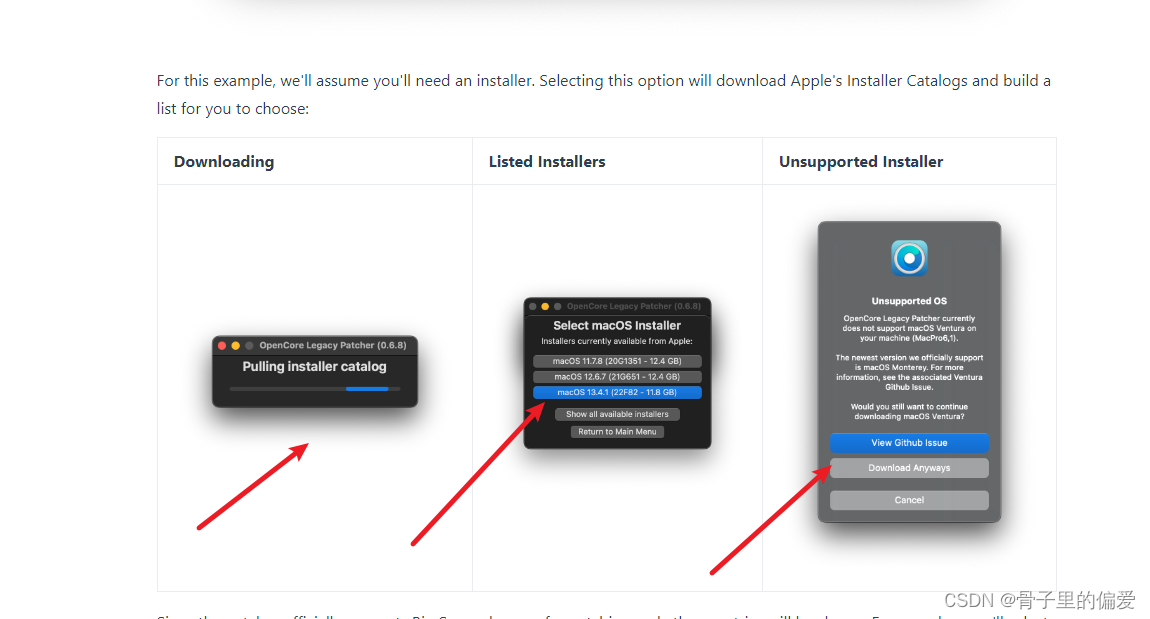
系统性风险
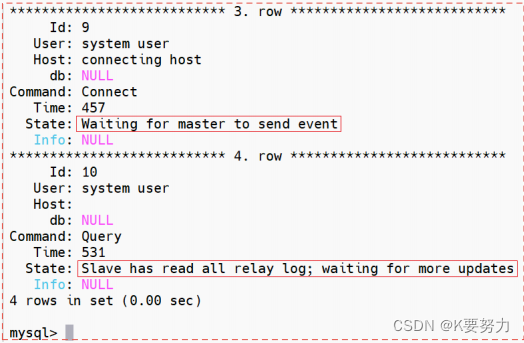
系统性风险(Systematic Risk)微观层面的定义由夏普(William Sharpe)在资本资产定价模型(CAPM)中首次提出,即资本市场中存在的不能通过分散投资予以消除的风险
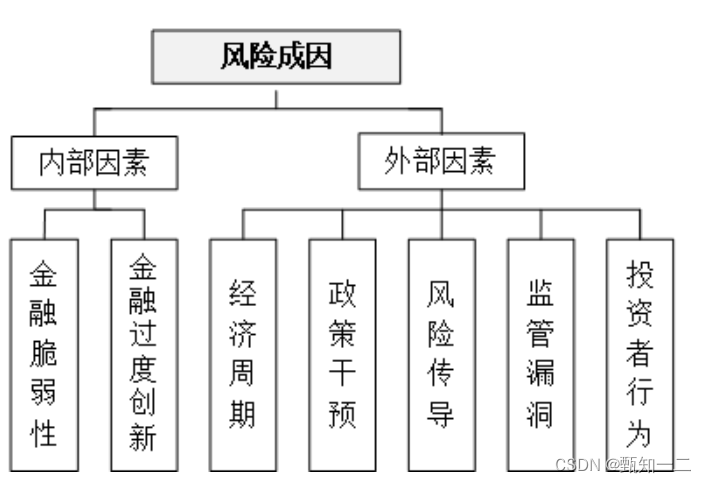
模型也会带来风险
详细介绍
1、线性关系(Linearity):两种资产之间存在非线性关系(如衍生品)时,相关性矩阵的运用会低估或高估分散化投资收益和风险
2、平稳性(Stationarity):相关性、波动率(BS公式等)和风险因子(周期性)这三个因子通常被认为是平稳的,但实际上可能是非平稳的
3、正态性(Normality):正态性是假设随机变量服从正态分布(也称高斯分布),在许多模型中,比如使用 -正态法计算VaR(Value at Risk)以及Black Scholes模型中的几何布朗运动都是假设市场收益率是服从正态分布的,但实际收益率分布呈现尖峰厚尾的特点,这意味着大多公司低估了尾部风险事件的数量,对于市场的冲击准备不够充足
4、样本偏差(Sampling Bias):样本偏差是指样本不能代表整体,通常是由于抽样选择方法的偏差引起的,意味着样本中任意事件发生的概率大于或小于该事件在整体中出现的概率。
5、过度拟合/欠拟合(Over and Under Fitting)
6、幸存者偏差(Survivorship Bias):幸存者偏差是对数据集进行统计分析时,该数据集只包含那些“存活”到某一特定时间点的实体。例如分析对冲基金产生的收益情况,有一些对冲基金因损失惨重而倒闭,如果研究过去三年对冲基金的收益情况,那仅包含目前还存续的对冲基金,并不包含失败的对冲基金,则数据集无法反映对冲基金的真实风险情况,这被称作生存者效应。
7、遗漏变量偏差(Missing Variable Bias):
数据窥视偏差
数据窥视( data-snooping )是指从数据中发现统计上显著但实际并不存在的关系,是金融分析里面非常普遍和严重的一个问题。在回测投资策略时,不管我们有没有选股思想,我们都可以不断通过调整现有参数或加入新的参数使某一策略在历史数据测试集的表现很好。
我们的投资策略最终是要面向未来市场环境的。策略的历史回测结果,仅仅是这个策略在过去的业绩,更多是给自己看的,没有必要过于追求策略过去的收益率而过度优化模型。我们应更加深入的认识了解市场,通过对市场的认知来理解模型与数据,来设计投资策略。在实际策略回测中,我们可以使用样本外测试来减少数据窥视偏差对投资决策的影响。
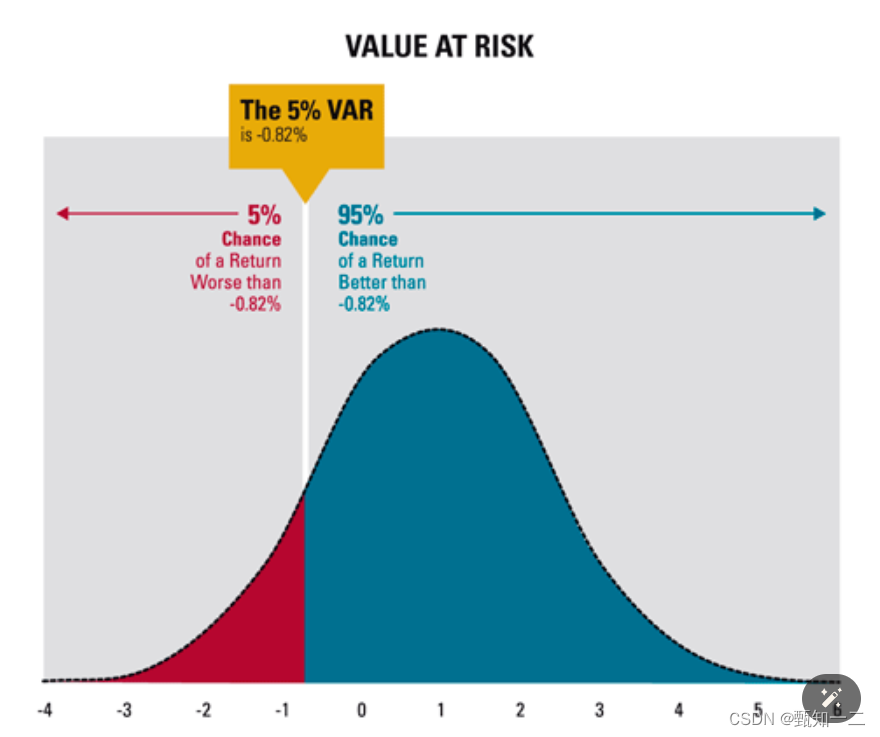
VaR(Value at Risk 风险价值)
VaR模型是指: “在一定概率的情形下,金融机构投资组合的价值在未来一定时间内最多可能损失多少”这一问题
步骤
计算VaR的关键在于确定资产组合未来损益的统计分布,计算过程由两部分构成:
1.映射过程:建立投资组合价值与风险因子之间的函数关系。
2.估值过程:根据风险因子的波动性或未来情景估计投资组合的未来损益分布。
分类
常见的VaR模型包括历史模拟法、参数法和蒙特卡罗模拟法等。
历史模拟法:
- 原理:用给定历史时期上所观测到的风险因子的变化来表示风险因子未来的变化,从而得到风险因子的未来n个数据,采用全值估计方法(full revaluation)即根据市场因子的未来价格水平对组合头寸进行重新估计, 进而得到组合价值未来损益的n个可能结果,根据得到的组合未来损益分布,通过分位数计算VaR。
- 步骤:选择历史时间段,从中提取资产价格变动序列。然后,根据这些序列构建未来价格的可能分布,并基于所选置信水平确定VaR。
步骤
- 计算成分股票收益率序列
- 计算股票组合收益率序列
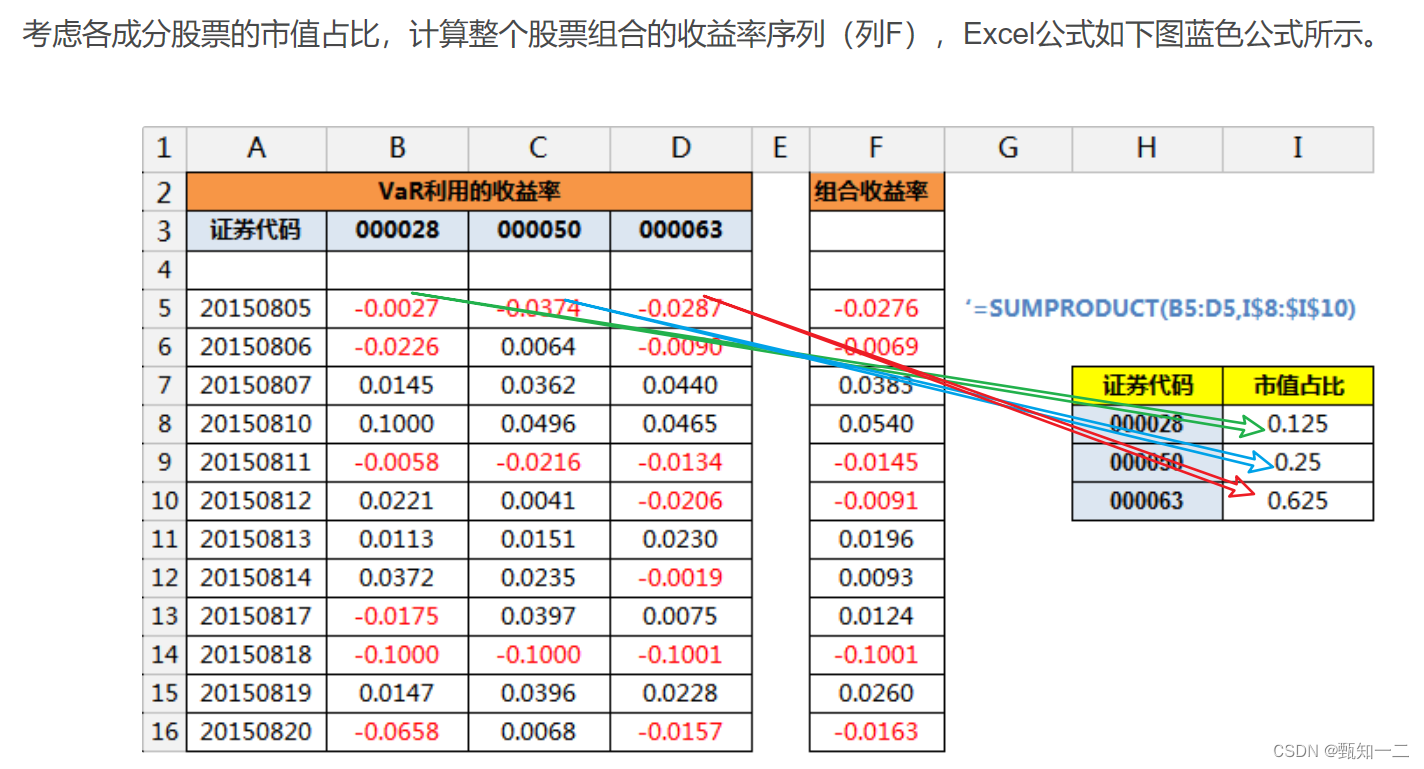
- 计算股票组合VaR(PERCENTILE.INC 是 Excel 中的一个统计函数,用于计算一组数据的某个百分位数。)

-
参数法:
- 原理:参数法基于对资产价格变动过程的数学建模,通常使用的模型包括几何布朗运动和扩散过程等。通过对这些模型的参数进行估计,可以推断未来的价格变动情况,并计算相应的VaR。
- 步骤:选择合适的数学模型,并根据历史数据对模型的参数进行估计。然后,使用这些参数构建未来价格的可能分布,并计算VaR。
-
蒙特卡罗模拟法:
- 原理:蒙特卡罗模拟法基于随机过程的概念,通过生成大量随机样本路径来模拟未来资产价格的可能变动情况。通过统计这些模拟路径中超过一定损失水平的比例,来估计VaR。
- 步骤:随机生成大量资产价格路径,并根据这些路径计算未来损失的分布。然后,基于所选的置信水平确定VaR。
-
优缺点
- 历史模拟法简单直观,但对于极端事件的处理可能不足;
- 参数法需要对资产价格变动过程进行合理的假设和建模,可能受到模型假设的影响;
- 蒙特卡罗模拟法能够更好地模拟复杂的价格变动情况,但计算成本较高。
投资组合的VaR
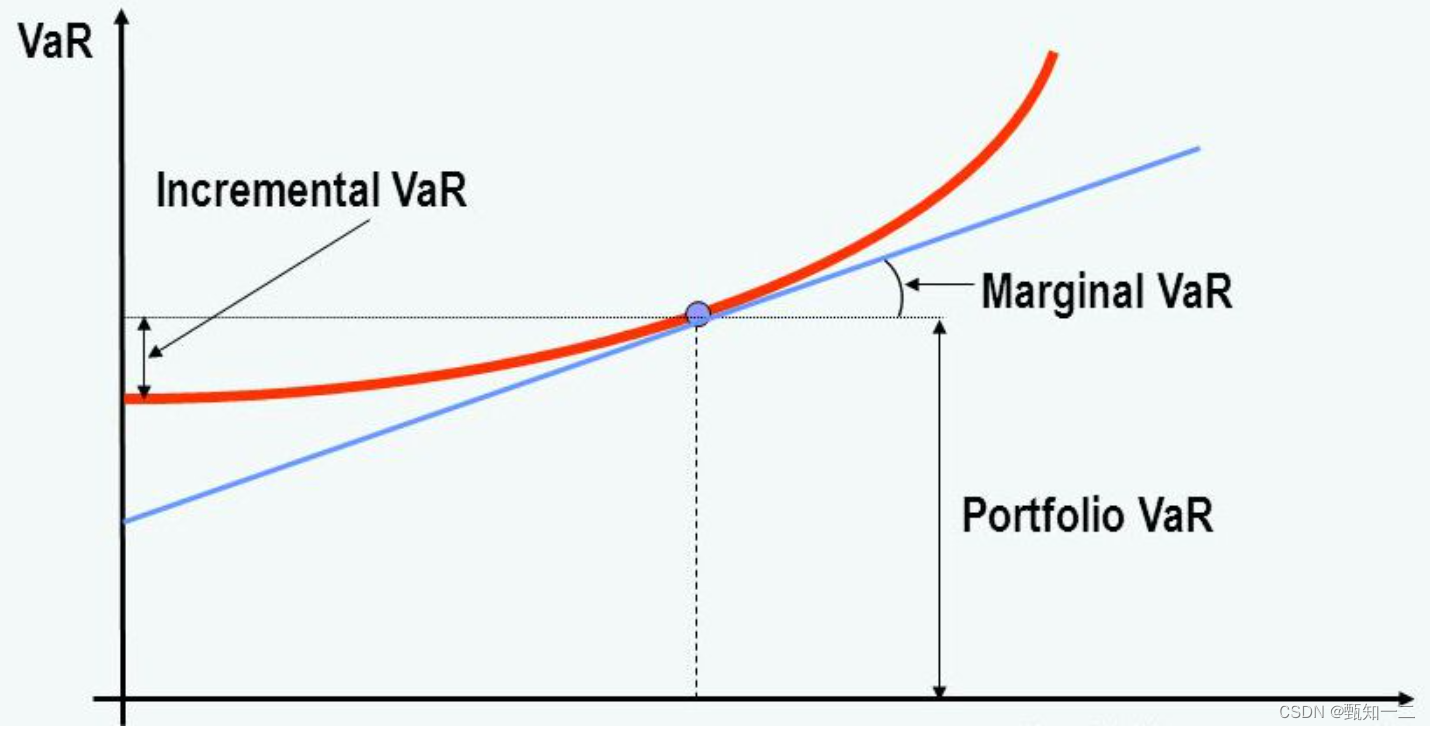
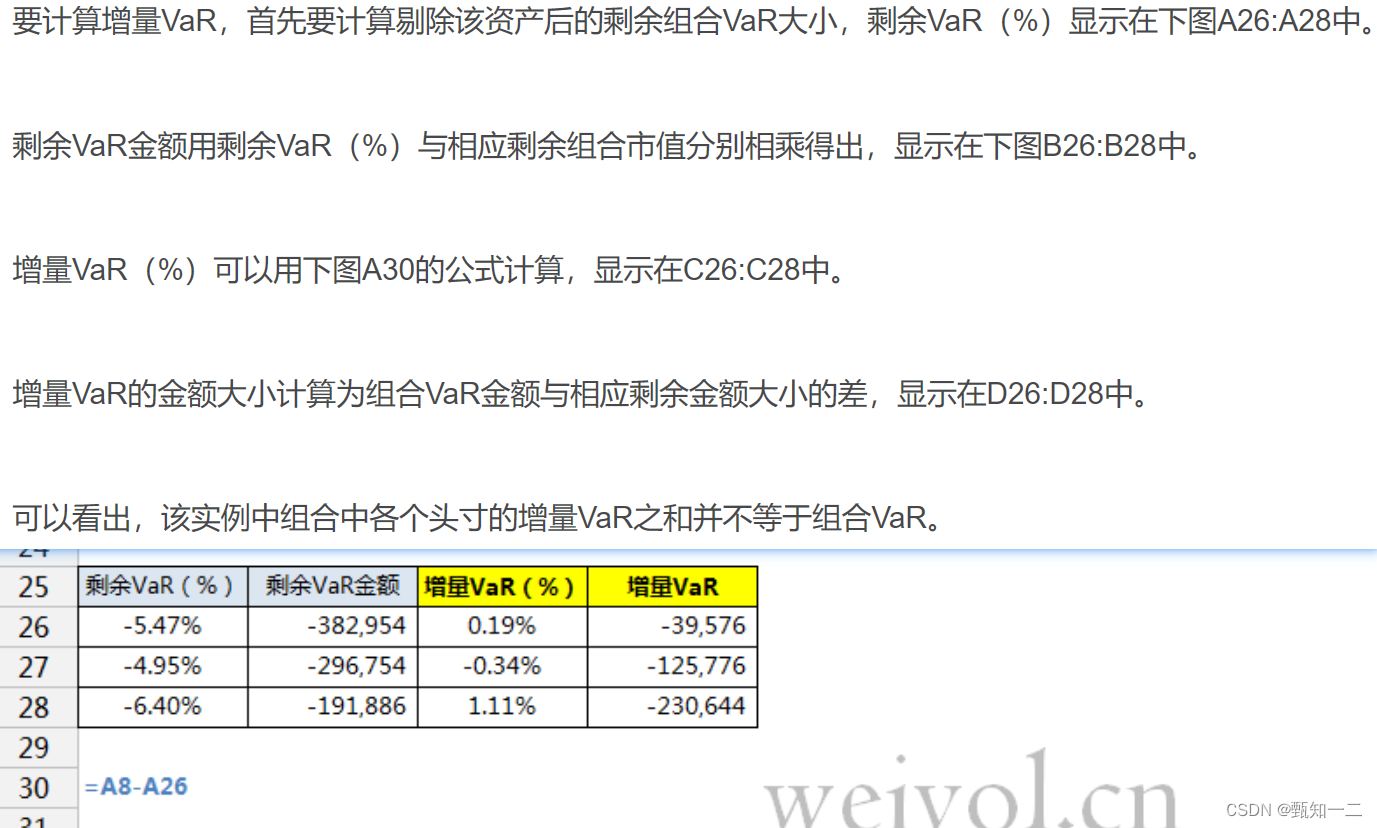
由于组合投资的分散化效应,组合中各资产的独立VaR之和一般不等于分散化后的组合VaR。
1、通过使用边际VaR(Marginal VaR),刻画了各个资产对投资组合VaR的边际贡献,反映的是组合中资产头寸变化的灵敏度,为投资者决策下一笔资金投资在哪里可以获得更好的效益提供了有效的信息。另外,当投资者计划减仓并尽量多的降低风险时,可以通过选取边际VaR最大的资产头寸进行操作。


2、通过使用成分VaR(Component VaR),我们可以了解投资组合中每个资产对分散化组合VaR的贡献,也就是对于一个组合VaR,组合中哪些资产贡献了最大的风险,哪些资产相反能“对冲”风险;

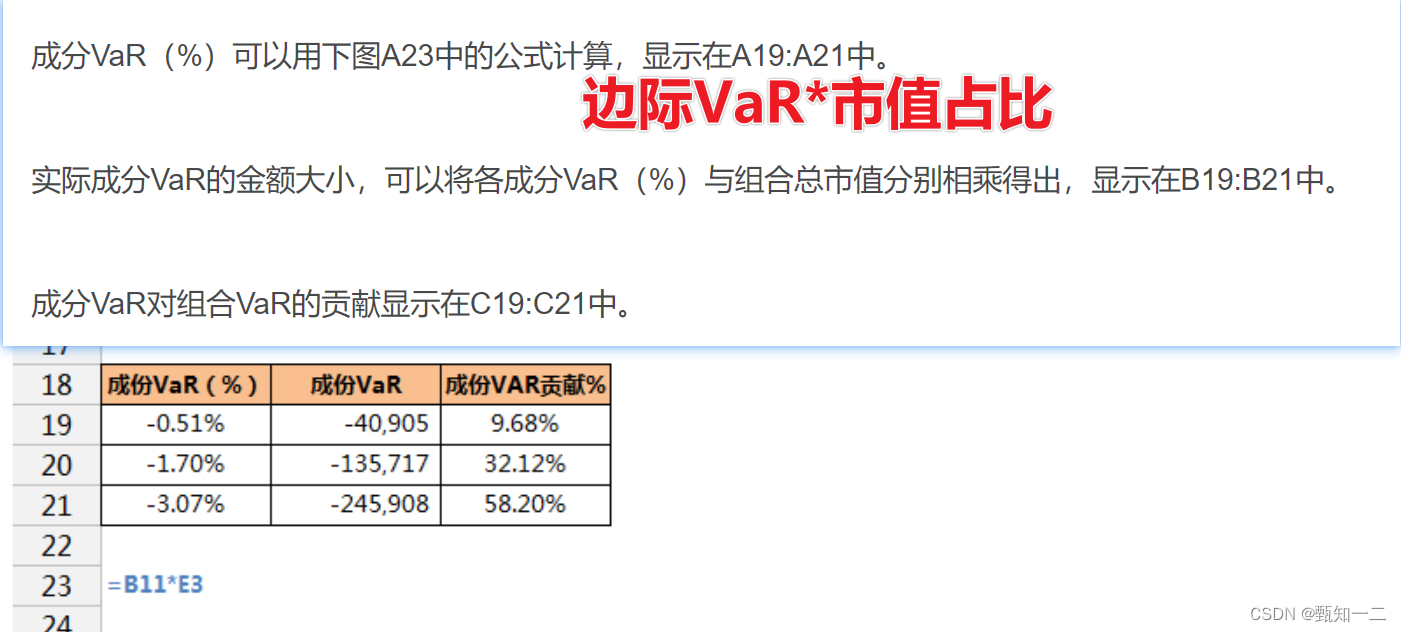
3、通过使用增量VaR(Incremental VaR),我们可以了解对现有组合增加一种新的资产,对组合VaR增量的影响,也就是说当一种新资产被增加到当前组合中,组合VaR增加或减少的大小。
ES(Expected Shortfall 期望损失)概述
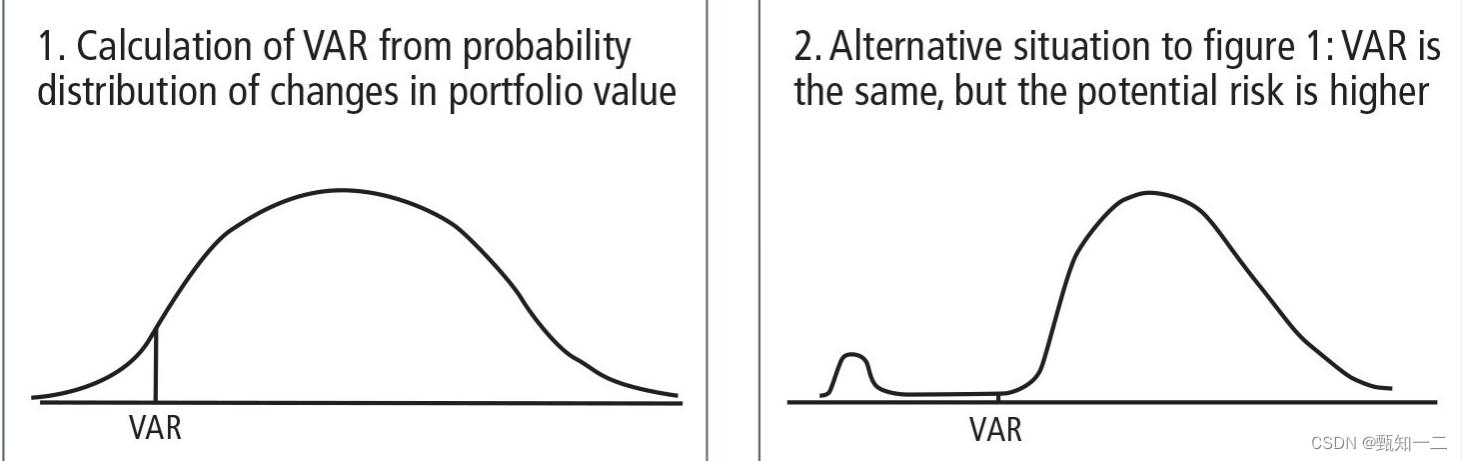
VaR的局限性导致其不具备度量投资组合尾部风险的能力,它将损失可能发生的概率限定为一个值,因此低估了实际的市场风险。
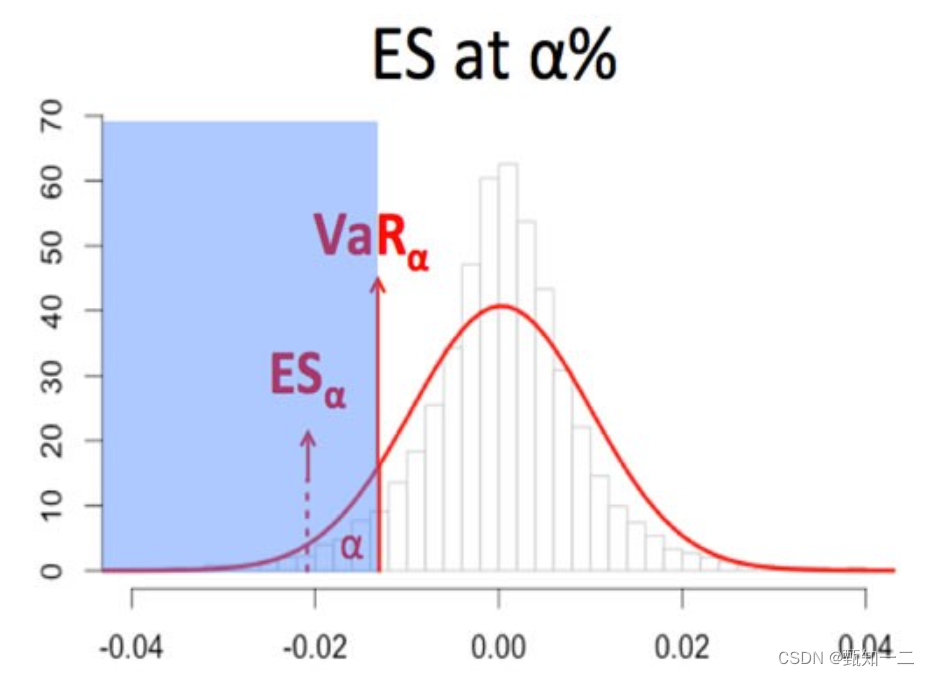
Expected Shortfall期望损失,又称Conditional VaR(条件风险价值),或称Expected Tail Loss(期望尾部损失),主要分析计算的内容为尾部损失的平均值。
ES的定义为:当投资组合的损失超过VaR损失(例如,上图所示α%的VaR)时所遭受的期望损失(即平均损失的大小)。
- 风险度量的“次可加性”:[股票组合1的风险值]+[股票组合2的风险值] ≥ [合并后股票组合的风险值]。(相比于各单独的股票组合,合为一组后股票组合的篮子更大,涵盖的股票种类以及对应的行业更多,风险分散的效果更好)
- 采用VaR计量风险不具备次可加性,投资组合的VaR在极端情况下,会大于两个独立组合的VaR之和。
- ES模型满足次可加性,可以更好地对风险进行计量。ES的这一特征使得对于一个大范围的风险控制可以分解到子单位上,只需要控制一个公司各个部门的ES,就控制了整个公司的ES。但VaR无法做到这一点。