今天,你读完这篇文章,普及组的动态规划已经可以秒了。
最长公共子序列
求两个数列的最长公共子序列(Longest Common Subsequence,LCS)的长度。
数列 X 和 Y 的最长公共子序列 Z,是指 Z 既是 X 的子序列,又是 Y 的子序列,而且任意长度超过 Z 的数列 Z∗ 都不符合这个性质。
状态定义
f[i][j]表示x[1]、x[2]……x[i]和y[1]、y[2]……y[j]的LCS
状态转移方程
若x[i]=y[j],f[i][j]=f[i-1][j-1]+1;
若x[i]!=y[j],f[i][j]=max(f[i-1][j],f[i][j-1]);

大家可以用滚动数组试试
回文词
给定一个字符串,问至少需要增加多少个字符,才能把这个字符串变成回文词。一个字符串是回文词,是指从前往后看和从后往前看是一样的。比如:abcba、abccba、bcaacb都是回文词,但 abc 不是回文词。
这道题是前一道题的衍生。
假设给定的字符串为s,将s反转,得到t。那么,答案就是:s长度-s和t的LCS。这里就不给代码了
最长上升子序列
朴素解法
f[i]表示以i结尾的最长上升子序列的长度
按照倒数第二个选谁分类:
我们先扫描i号元素前的每个元素(正向),找出第一个比i号元素小的元素k号。①仍然选i号元素,f[i]。②选k号,f[k]+1
但是,这种解法时间复杂度为O(N^2),一但长度到200,就会扣分,我们这次就讨论O(nlog n)的算法。
优化解法
不升子序列最小划分数
我们用贪心解决这个问题。定义d[i]为第i条不升子序列的最后一个数,cnt代表有几个子序列
我们先扫描每个数字x[i],再枚举每一个子序列,判断是否能接在某个子序列后,如果不行,则新增一个序列即可。
#include <bits/stdc++.h>
#define N 1005
using namespace std;
int n,i,j,d[N],x[N];
int main(){
cin>>n;
for(int i=0;i<n;i++) cin>>x[i];
int cnt=0;
for(i=0;i<n;i++){
for(j=0;j<cnt;j++)
if(d[j]>=x[i]) break;
d[j]=x[i];
if(j==cnt) cnt++;
}
cout<<cnt<<endl;
return 0;
}O(N^2)的算法,显然要优化
不妨试试二分
#include <bits/stdc++.h>
#define N 1005
#define INF 2e9
using namespace std;
int n,d[N],x[N];
int main(){
cin>>n;
for(int i=0;i<n;i++) cin>>x[i];
fill(d,d+n,INF);
for(i=0;i<n;i++)
*lower_bound(d,d+n,x[i])=x[i];
int cnt=lower_bound(d,d+n,INF)-d;
cout<<cnt<<endl;
return 0;
}大家可能就纳闷了:这玩意和LIS有神马关系???
Dilworth反链
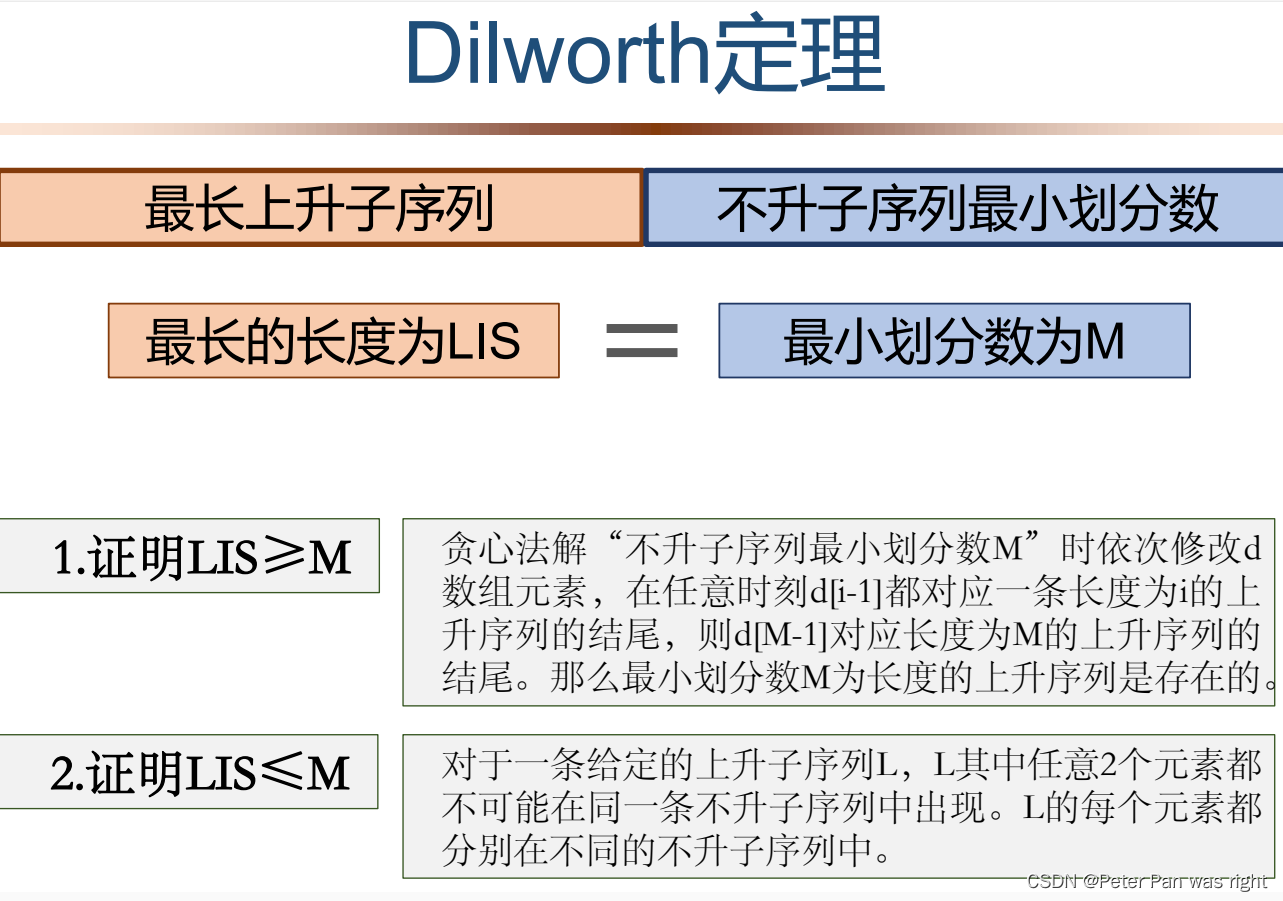
LIS为最长子序列, 那么说明一定能找到LIS个数,从左往右是递增的。那么这些树一定不能放在同一组内,不然与不升矛盾。到目前为止,每个数单独为一组,已经开了LIS组了。说明任何一种满足要求的分组,组数都>=LIS。
这一下子,LIS算法就从O(N^2)降到了O(NlogN)
航线问题
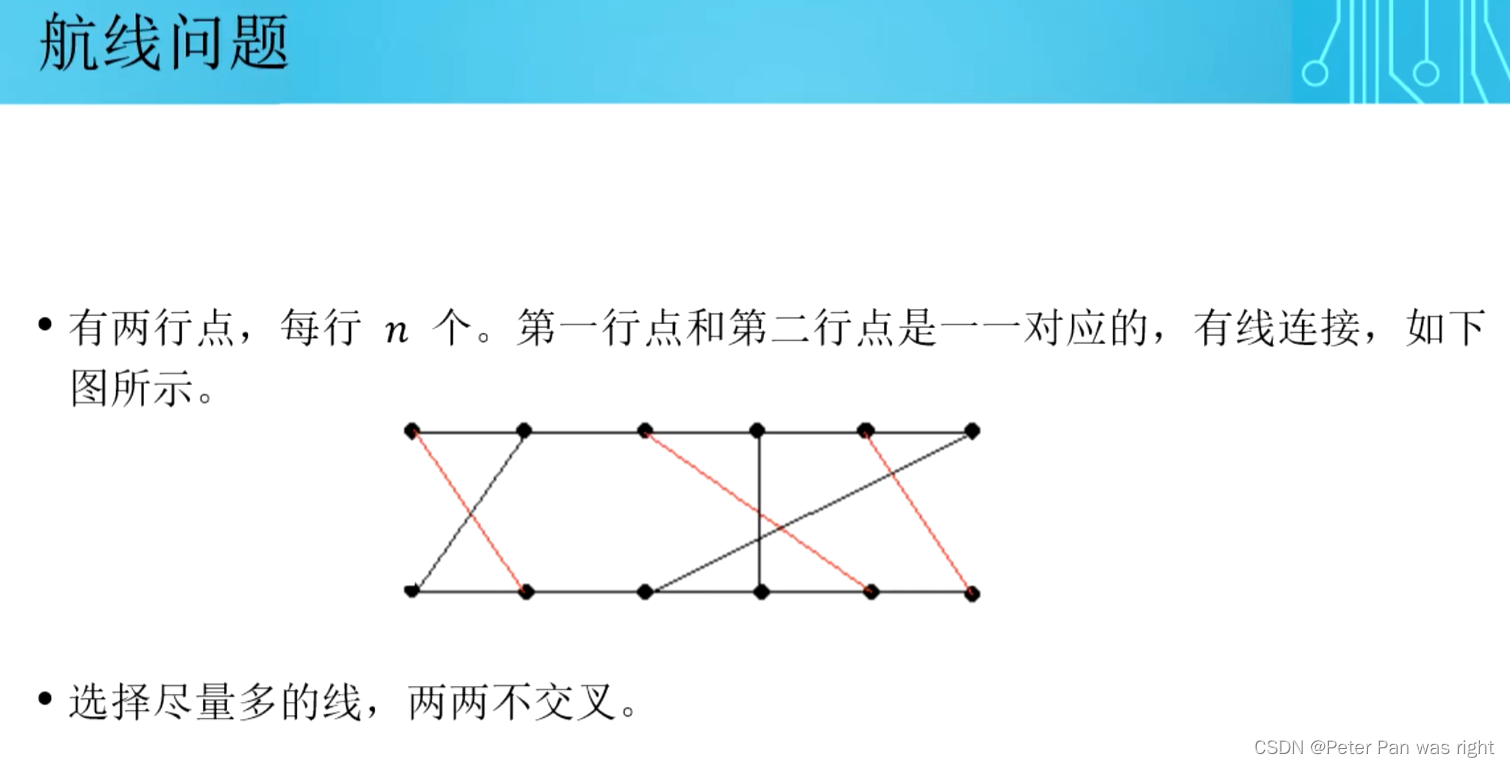
这道题是上一道题的衍生。
设第1行第i个点对应第2行第f[i]个点。假设i<j,则两条线(i,f[i])和(j,f[j])不相交的充要条件是f[i]<f[j],于是问题变为求f的LIS了,这里就不发代码了。
两个排列的LCS
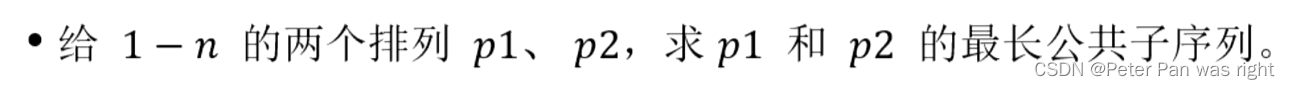
我们可以把两个排列作相同的置换。如p1:1 5 3 2 4变成1 2 3 4 5,即做置换5→2,2→4,4→5,
于是我们可以将p1置换成1 2 ……n,p2做相同的置换,则问题就变为LIS了,时间复杂度O(N^2)
摆花
原题链接:P1077 [NOIP2012 普及组] 摆花 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)
我们可以把问题抽象化:有 n 个数(c1,c2,...,cn),0⩽ci⩽ai,求有多少种方案数使
就变成经典dp了,
然后可以使用前缀和优化
乘积最大
原题链接:P1018 [NOIP2000 提高组] 乘积最大 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)
这道题,我只给代码,大家自己思考一下
#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std;
long long f[45][60];
string in;
int n,k;//n位数 k个乘号
long long g[45];
long long cut(int l,int r){
long long end = 0;
for(int i = l;i <= r;i++)
end = end * 10 + g[i];
return end;
}
int main(){
cin >> n >> k >> in;
for(int i = 1;i <= n;i++)
g[i] = in[i - 1] - '0';
for(int i=1;i<=n;i++)
f[i][0] = cut(1,i);
for(int i = 2;i <= n;i++){ //枚举分割为前i位数字
for(int a = 1;a <= min(i-1,k);a++){ //枚举有几个乘号
for(int b = a;b < i;b++){ //在第几位放乘号
f[i][a] = max(f[i][a],f[b][a-1] * cut(b + 1,i));
}
}
}
cout<<f[n][k];
return 0;
}反逆序对问题
给定 n,k,求在所有长度为 n的排列中,有多少排列的逆序对恰好为 k 。
给出表答(懒得打LateX)

#include <bits/stdc++.h>
#define ll long long
using namespace std;
const int Maxn=10100;
const ll Mod=1e9+7;
int n,k;
ll f[Maxn],sm[Maxn];
int main(){
scanf("%d%d",&n,&k);
f[0]=1;
for(int i=1;i<=n;i++){
sm[0]=f[0];
for(int j=1;j<=k;j++) sm[j]=(sm[j-1]+f[j])%Mod;
for(int j=0;j<=k;j++){
if(i>j) f[j]=sm[j];
else f[j]=(sm[j]-sm[j-i]+Mod)%Mod;
}
}
printf("%lld",f[k]);
return 0;
}今天的题目就是这么简单,祝大家早日AC
彩蛋
给定一个十进制整数 n,保证 n 的首位不为 00,你必须删除其中 d 个数字,使得留下的数字最大。请输出留下的最大数。