stack的介绍和使用

非成员函数
例题
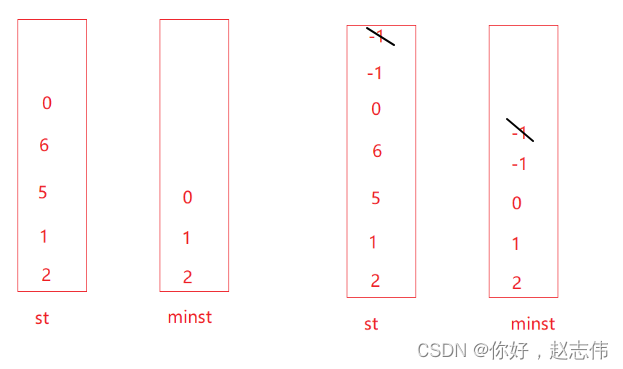
最小栈
解析
用另一个栈minst去存储st的最小值,当st每插入一个数是新的最小值(相同也是)就同时插入minst,释放这个最小值时minst同时释放
栈的压入、弹出序列
输入两个整数序列,第一个序列表示栈的压入顺序,请判断第二个序列是否可能为该栈的弹出顺序。假设压入栈的所有数字均不相等。例如序列1,2,3,4,5是某栈的压入顺序,序列4,5,3,2,1是该压栈序列对应的一个弹出序列,但4,3,5,1,2就不可能是该压栈序列的弹出序列。
1. 0<=pushV.length == popV.length <=1000
2. -1000<=pushV[i]<=1000
3. pushV 的所有数字均不相同
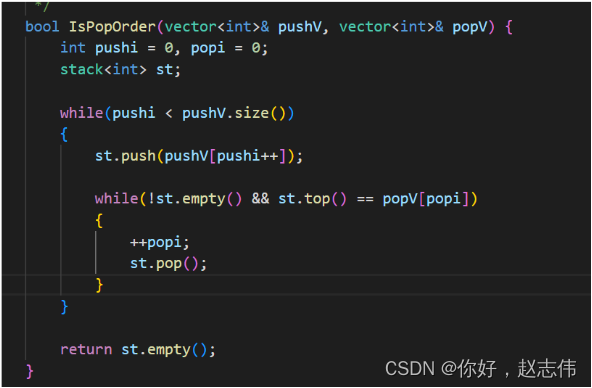
解析:
1.先把入栈序列入列
2.栈顶元素和出栈序列是否匹配
a.如果匹配,持续出数据,直到不匹配或者栈为空
b.如果不匹配,继续入数据
结束标志
入栈序列走完了,再来判断
1.栈为空或出栈序列到尾则返回true
2.栈不为空或出栈序列没有到尾返回false
逆波兰表达式求值
给你一个字符串数组
tokens,表示一个根据 逆波兰表示法 表示的算术表达式。请你计算该表达式。返回一个表示表达式值的整数。
注意:
- 有效的算符为
'+'、'-'、'*'和'/'。- 每个操作数(运算对象)都可以是一个整数或者另一个表达式。
- 两个整数之间的除法总是 向零截断 。
- 表达式中不含除零运算。
- 输入是一个根据逆波兰表示法表示的算术表达式。
- 答案及所有中间计算结果可以用 32 位 整数表示。
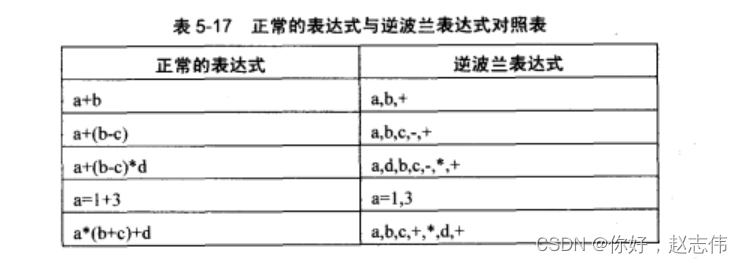
逆波兰表达式又叫做后缀表达式。逆波兰表示法是波兰逻辑学家J・卢卡西维兹于1929年首先提出的一种表达式的表示方法。后来,人们就把用这种表示法写出的表达式称作“逆波兰表达式”。逆波兰表达式把运算量写在前面,把算符写在后面。
逆波兰表达式计算
由内圈向外圈
用栈计算
逆波兰表达式的转换
用栈转换
1.操作数输出
2.操作符
a.栈为空吗,入栈
b.比栈顶的操作符优先级高,入栈
c.比栈顶的操作符优先级低或相等,出栈顶操作符,重复执行2操作
结束后,将栈中操作符全部出栈输出
遇见括号则走递归,解决括号中表达式
stack的模拟实现
#include<iostream> using namespace std; #include<vector> #include<list> namespace bit { // 设计模式 // 适配器模式 -- 转换 //适配器是一种设计模式(设计模式是一套被反复使用的、多数人知晓的、经过分类编目的、代码设计 //经验的总结),该种模式是将一个类的接口转换成客户希望的另外一个接口。 // stack<int, vector<int>> st1; // stack<int, list<int>> st2; template<class T, class Container = vector<T>> class stack { public: void push(const T& x) { _con.push_back(x); } void pop() { _con.pop_back(); } size_t size() { return _con.size(); } bool empty() { return _con.empty(); } const T& top() { return _con.back(); } private: Container _con; };
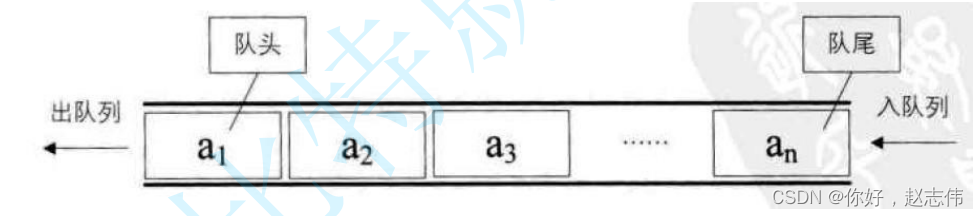
queue的介绍和使用

非成员函数
queue的模拟实现
#include<iostream> using namespace std; #include <list> namespace bit { template<class T, class Container = list<T>> class queue { public: queue() {} void push(const T& x) { _c.push_back(x); } void pop() { _c.pop_front(); } T& back() { return _c.back(); } const T& back()const { return _c.back(); } T& front() { return _c.front(); } const T& front()const { return _c.front(); } size_t size()const { return _c.size(); } bool empty()const { return _c.empty(); } private: Container _c; }; }
STL标准库中stack和queue的底层结构
虽然 stack 和 queue 中也可以存放元素,但在 STL 中并没有将其划分在容器的行列,而是将其称为 容器适配 器 ,这是因为 stack 和队列只是对其他容器的接口进行了包装, STL 中 stack 和 queue 默认使用 deque。
deque( 双端队列 ) :是一种双开口的 " 连续 " 空间的数据结构 ,双开口的含义是:可以在头尾两端进行插入和删除操作,且时间复杂度为O(1) ,与 vector 比较,头插效率高,不需要搬移元素;与 list 比较,空间利用率比较高。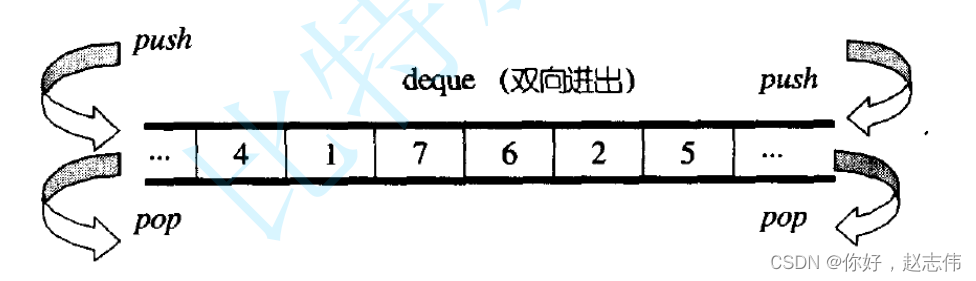
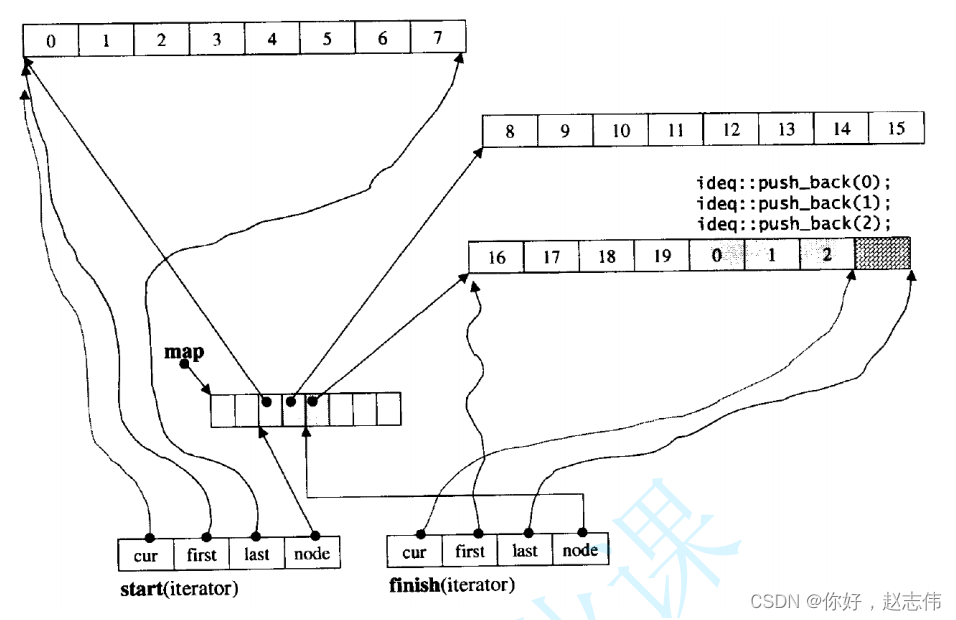
deque并不是真正连续的空间,而是由一段段连续的小空间拼接而成的,实际deque类似于一个动态的二维数组,其底层结构如下图所示:
双端队列底层是一段假象的连续空间,实际是分段连续的,为了维护其 “ 整体连续 ” 以及随机访问的假象,落 在了 deque 的迭代器身上, 因此 deque 的迭代器设计就比较复杂,如下图所示
deque的缺陷
与 vector 比较 , deque 的优势是:头部插入和删除时, 不需要搬移元素,效率特别高 ,而且在 扩容时,也不 需要搬移大量的元素 ,因此其效率是必 vector 高的。与 list 比较 ,其底层是连续空间, 空间利用率比较高 ,不需要存储额外字段。但是, deque 有一个致命缺陷:不适合遍历,因为在遍历时, deque 的迭代器要频繁的去检测其是否移动到 某段小空间的边界,导致效率低下 ,而序列式场景中,可能需要经常遍历,因此 在实际中,需要线性结构 时,大多数情况下优先考虑 vector 和 list , deque 的应用并不多,而 目前能看到的一个应用就是, STL 用其作 为 stack 和 queue 的底层数据结构
为什么选择 deque 作为 stack 和 queue 的底层默认容器stack 是一种后进先出的特殊线性数据结构,因此只要具有 push_back() 和 pop_back() 操作的线性结构,都可以作为stack 的底层容器,比如 vector 和 list 都可以; queue 是先进先出的特殊线性数据结构,只要具有push_back和 pop_front 操作的线性结构,都可以作为 queue 的底层容器,比如 list 。但是 STL 中对 stack 和queue默认选择 deque 作为其底层容器,主要是因为:1. stack 和 queue 不需要遍历 ( 因此 stack 和 queue 没有迭代器 ) ,只需要在固定的一端或者两端进行操作。2. 在 stack 中元素增长时, deque 比 vector 的效率高 ( 扩容时不需要搬移大量数据 ) ; queue 中的元素增长时,deque 不仅效率高,而且内存使用率高。结合了deque 的优点,而完美的避开了其缺陷。