Problem: 22. 括号生成

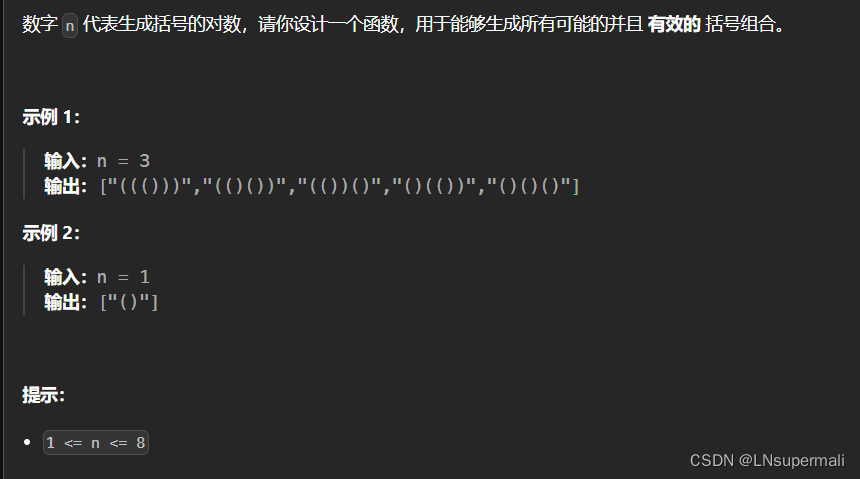
题目描述

思路

1.定义回溯函数：void backtrack(int n, int leftUsed, int rightUsed, int k, string& path)；(每个参数的具体说明见下面代码)

1.1.结束条件：当k == 2 * n时将path添加到结果集合result中；
1.2.回溯执行：当leftUsed < n时继续添加左括号到path上并继续回溯（此时，leftUsed加一表示有用掉一个左括号，k + 1表示进入下一层决策阶段），最后撤销选择；
1.3.回溯执行:当rightUsed < leftUsed时继续添加右括号到path上并继续回溯(此时rightUsed加一表示用掉一个右括号，k + 1表示进入下一层决策阶段)，最后撤销选择；

复杂度

时间复杂度:

$O\left(\frac{4^n}{\sqrt{n}}\right)$

空间复杂度:

$O\left(\frac{4^n}{\sqrt{n}}\right)$

Code

class Solution {
    vector<string> result;
public:
    /**
     * Get all parentheses generated
     * @param n The num of parenthesis
     * @return vector<string>
     */
    vector<string> generateParenthesis(int n) {
         string path;
         backtrack(n, 0, 0, 0, path);
         return result;
    }

    /**
     * Use backtracking to get all parentheses generated
     *
     * @param n The num of parenthesis
     * @param leftUsed The number of left parentheses used
     * @param rightUsed The number of right parentheses used
     * @param k         Decision stage
     * @param path      Decision path
     */
    void backtrack(int n, int leftUsed, int rightUsed, int k, string& path) {
        if (k == 2 * n) {
            result.push_back(path);
            return;
        }
        if (leftUsed < n) {
            path += '(';
            backtrack(n, leftUsed + 1, rightUsed, k + 1, path);
            path.pop_back();
        }
        if (rightUsed < leftUsed) {
            path += ')';
            backtrack(n, leftUsed, rightUsed + 1, k + 1, path);
            path.pop_back();
        }
    }
};