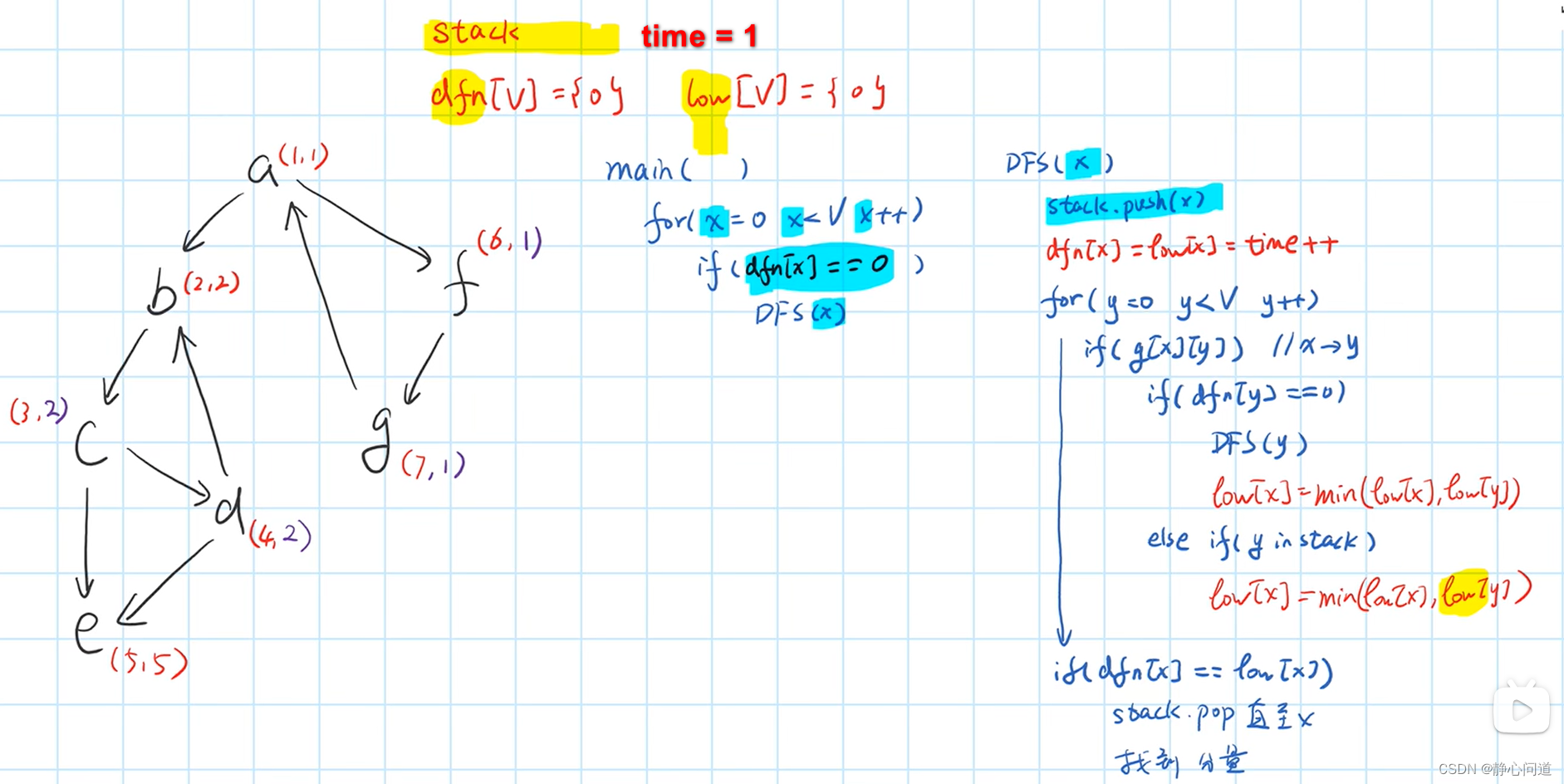
3.字符迁移【算法赛】 - 蓝桥云课 (lanqiao.cn)
问题描述
小蓝最近获得了一个长度为N 的字符串S,他对它爱不释手。
小桥为了考验小蓝对字符串的处理能力,决定给他提出一个挑战,她会进行 Q次操作:
每次操作给定三个整数 l , r , k ,将 S 的第 l 个字符到第 r 个字符都循环右移 k 次。
小桥想让小蓝回答她在操作完成后 S 是多少?小蓝陷入了困境,于是请你帮帮他!
字符右移表示为按字母表进行移动,例如 a 右移 1 次变为 b,b 右移 2 次变为 d。特别地,z 右移 1次变回为 a。
输入格式
输出格式
输出一个字符串表示答案
#include <iostream>
#include <cstring>
using namespace std;
const long long N = 2e5 + 10;
long long diff[N];
int main() {
long long n, q;
cin >> n >> q;
string s;
cin >> s;
while(q--) {
long long l, r, k;
cin >> l >> r >> k;
diff[l]+=k;
diff[r+1]-=k;
}
for(long long i=1;i<=n;i++){
diff[i]+=diff[i-1];
}
for (long long i = 0; i < n; i++) {
s[i] = (s[i] - 'a' + diff[i + 1]) % 26 + 'a';
}
cout << s << endl;
return 0;
}
总结:
- 暴力会超时
- 像这种区间同时变化的题,想想差分和前缀和
- 字符右移是循环,所以%26
差分和前缀和:
一维前缀和
S[i] = a[1] + a[2] + ... a[i]
a[l] + ... + a[r] = S[r] - S[l - 1]二维前缀和
S[i, j] = 第i行j列格子左上部分所有元素的和
以(x1, y1)为左上角,(x2, y2)为右下角的子矩阵的和为:
S[x2, y2] - S[x1 - 1, y2] - S[x2, y1 - 1] + S[x1 - 1, y1 - 1]一维差分
给区间[l, r]中的每个数加上c:B[l] += c, B[r + 1] -= c
二维差分
给以(x1, y1)为左上角,(x2, y2)为右下角的子矩阵中的所有元素加上c:
S[x1, y1] += c, S[x2 + 1, y1] -= c, S[x1, y2 + 1] -= c, S[x2 + 1, y2 + 1] += c