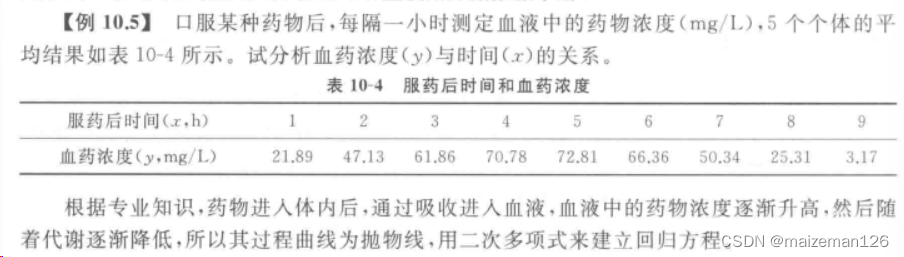
参考资料：生物统计学

        多项式回归属于单变量曲线回归，但其形式和求解方法与多元线性回归相似。多项式回归的数学模型为：

令，，，，则

        由于X不可逆，两边同时乘以X'得，，两边在同时乘以X'X的逆矩阵，则：

        进行回归方程的显著性检验时，可以直接用原始数据计算平方和：

        检验偏回归系数的显著性时，,为矩阵对角线上的元素。和多元线性回归一样，当检验结果存在不显著的偏回归系数时，需逐步剔除不显著的项重新建立回归方程。

        如果令，则多元线性回归方程和多项式回归方程的形式一致，多元线性回归方程也可以直接用原始数据求解。

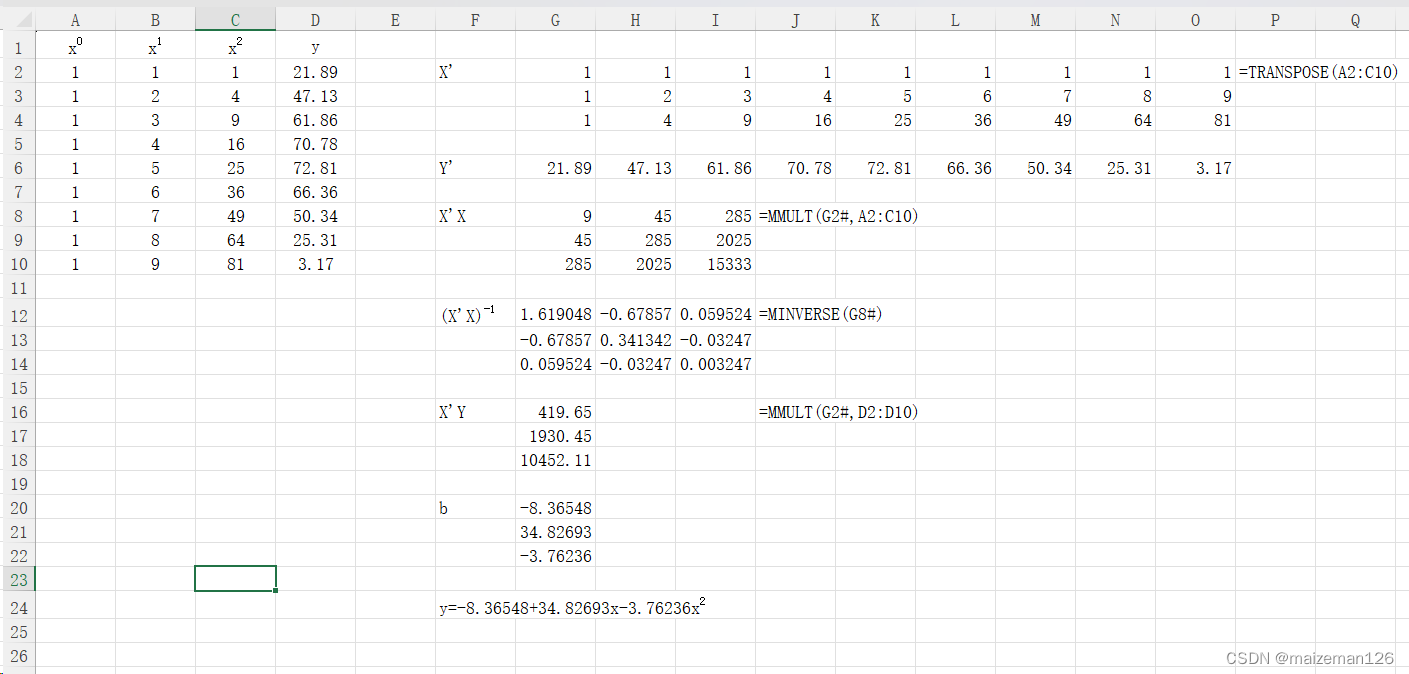
excel操作如下：

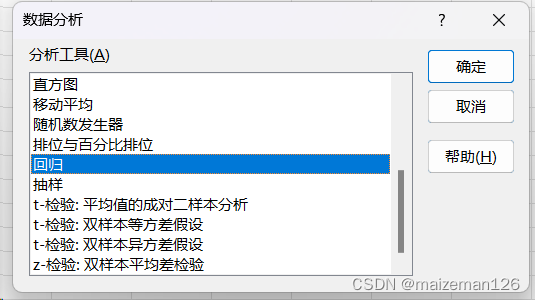
当然可以用数据分析工具直接求得偏回归系数和进行显著性检验，如下：

1、在数据分析工具对话框中，选择“回归”

2、选择对应的输入和输出区域。此处注意X值的输入区域不用选择列，只选择和列的数据。

3、导出结果

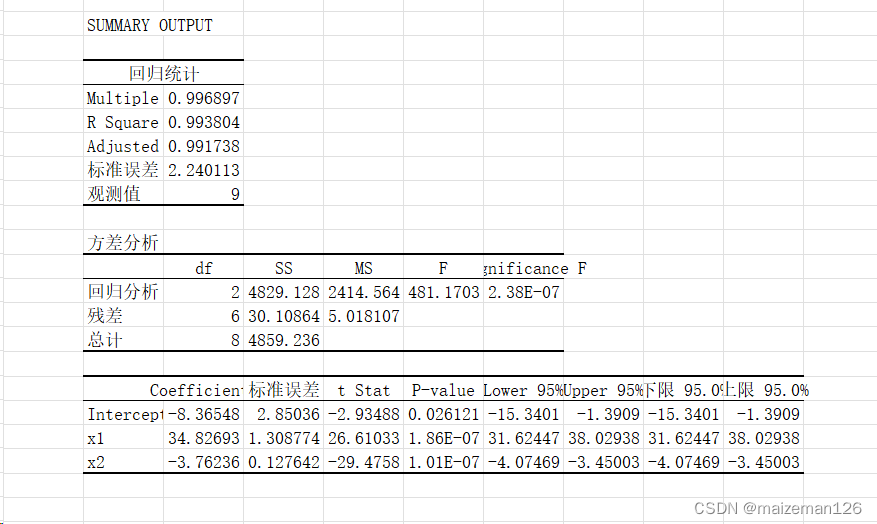
4、结果显示

        回归方程显著，即存在回归关系；截距和两个偏回归系数均显著，表明y和x之间存在二次曲线回归关系。