https://blog.csdn.net/qq_41682922/article/details/85013008

https://blog.csdn.net/guoziqing506/article/details/81328402

https://www.cnblogs.com/cymx66688/p/11363163.html  参数详解

逻辑回归的引出：

数据线性可分可以使用线性分类器，如果数据线性不可分，可以使用非线性分类器。但是对于一个二分类问题，如果我们不仅想知道一个具体的样例是属于哪一类，而且还想知道该类属于某一类的概率多大，有什么办法呢？逻辑回归使用回归的思想来处理分类问题。

逻辑回归：

                                      z= w_0+w_1x_1 + w_2x_2 + w_3x_3 + … + w_nx_n

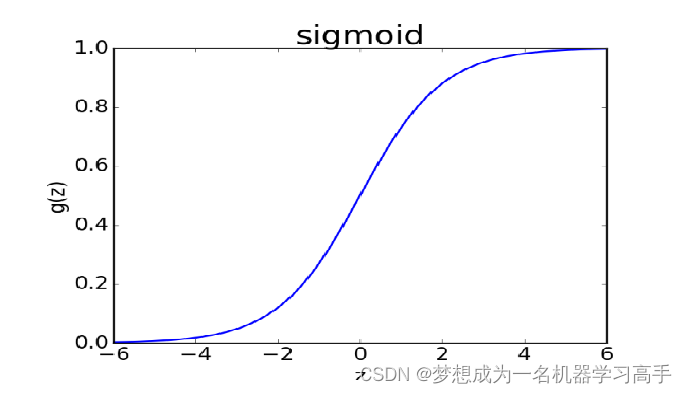
z的阈值处于(-∞，+ ∞)，此时不能很好的给出属于某一类的概率，因为概率的范围在[0,1]之间，并且这个函数能够具有很好的可微分性。在这种需求下，人们找到了这个映射函数，即 Sigmoid 函数，其形式如下：

逻辑回归的目标函数 ：

需求分析：对于一个二分类问题，我们关心的是根据自变量的值来对 Y 的取值 0 或 1 进行预测。

逻辑回归模型得到的只是 p{Y=1l x} 的预测概率。一般以0.5为界限，预测大于0.5时，我们判断此时 Y 更可能为1，否则认为 Y =0。

假设 Sigmoid 函数 Φ(z) 表示属于1类的概率， 于是做出如下的定义：

将两个式子综合起来可以改成为下式：

逻辑回归的损失函数 ：

目的分析：因为逻辑回归是为了解决二分类问题，即我们的目的应该是求取参数 w 和 b 使得 p(y l x) 对 0 类和 1 类的分类结果尽可能取最大值。然而我们定义损失函数时往往是为了最大化的达到我们的目的的同时使所付出的代价最小 （损失函数最小）。于是很自然地在目的函数前加一个负号就得到了我们逻辑回归的损失函数：

 根据损失函数是单个样本的预测值和实际值的误差，而成本函数是全部样本的预测值和实际值之间的误差，于是对所有样本的损失值取平均，得到我们的成本函数：

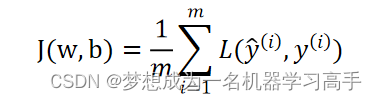
代码实现： 

from sklearn.linear_model import LogisticRegression
from sklearn.datasets import load_wine
data = load_wine()
lr = LogisticRegression()

X = data.data
y = data.target

from sklearn.model_selection import train_test_split

X_train,X_test,y_train,y_test = train_test_split(X,y,test_size=0.3)
lr.fit(X_train,y_train)

print(lr.predict(X_test))

print(lr.predict_proba(X_test))