目录
0.前言
1.认识带环链表
2.带环链表OJ问题简述
3.判断是否为带环链表
4. 寻找入环节点(法一:数学推理的魅力)
5. 寻找入环节点(暴力拆解带环链表的魄力)
6.番外:判断是否为带环链表(fast和slow的速度选择)
0.前言
本文所有代码及图片资源都已传入gitee,可自取
3链表OJ题p3(带环问题) · onlookerzy123456qwq/data_structure_practice_primer - 码云 - 开源中国 (gitee.com)![]() https://gitee.com/onlookerzy123456qwq/data_structure_practice_primer/tree/master/3%E9%93%BE%E8%A1%A8OJ%E9%A2%98p3(%E5%B8%A6%E7%8E%AF%E9%97%AE%E9%A2%98)
https://gitee.com/onlookerzy123456qwq/data_structure_practice_primer/tree/master/3%E9%93%BE%E8%A1%A8OJ%E9%A2%98p3(%E5%B8%A6%E7%8E%AF%E9%97%AE%E9%A2%98)
1.认识带环链表
链表带环问题是一个非常经典的链表OJ题,本文将会进行细致剖析,首先第一个问题:什么是带环的链表呢?
我们通常说的单链表是一个节点一个节点线性连接的,最后一个节点指向NULL,代表这个单链表的结束。带环链表偏偏不这样,其最后一个节点并不指向NULL,而是又回来指向该单链表中的某个节点。
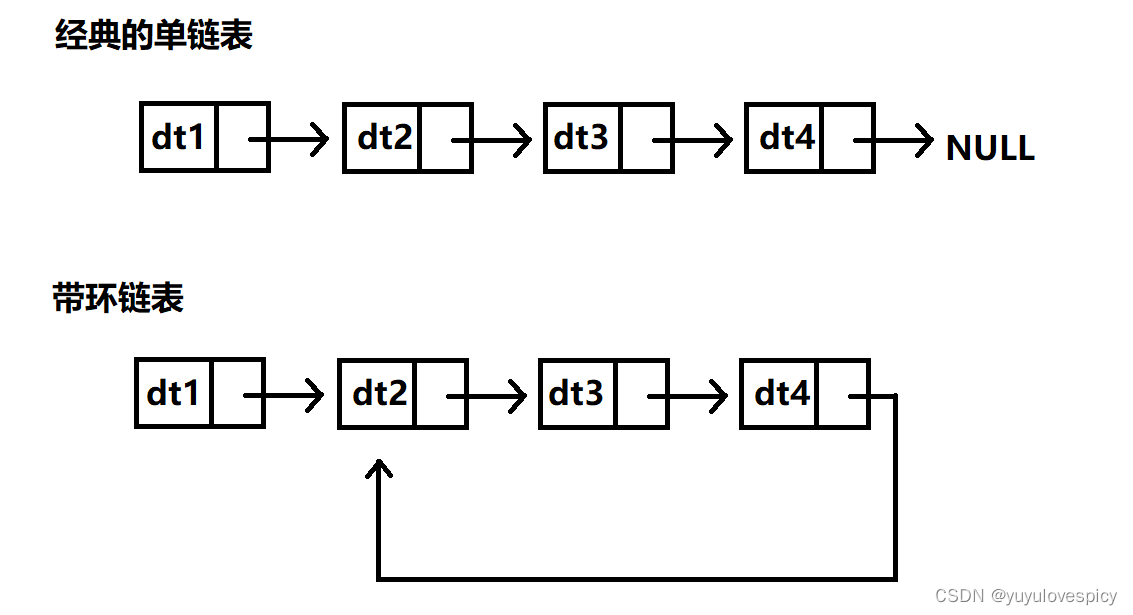
这样就会导致一个非常严重的问题!!!经典的单链表你用cur去遍历这个链表是可以用while(cur){cur = cur->next;}遍历到尾NULL结束的,但是你现在对带环链表进行遍历的话,那cur就永远也走不到NULL了,就相当于cur一直在这个环里一直转圈!!!陷入死循环。
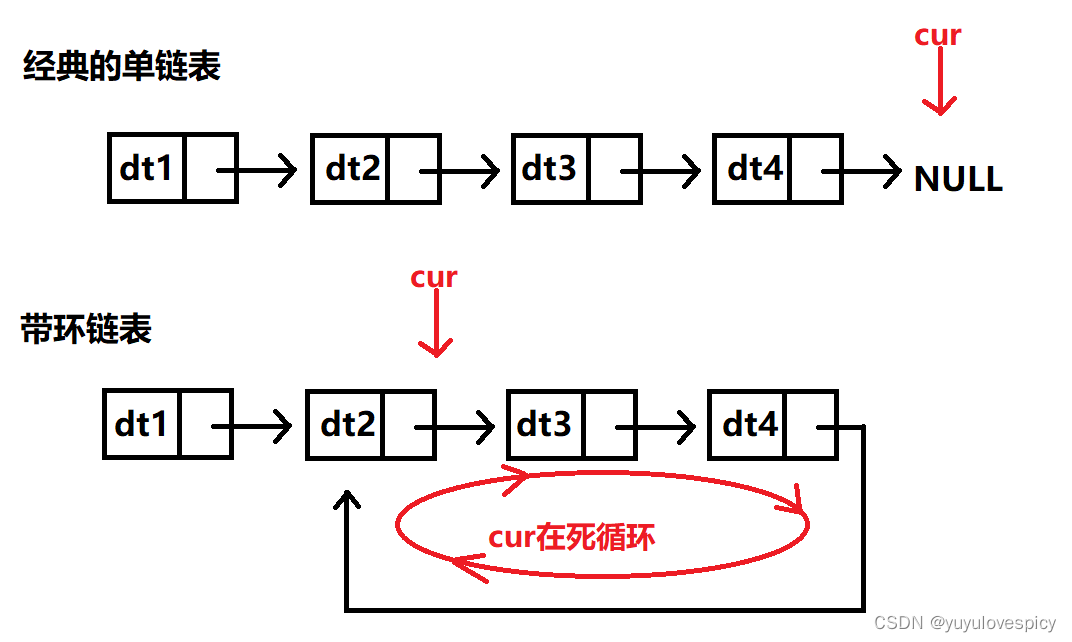
这就是带环链表的特点。
2.带环链表OJ问题简述
141. 环形链表 - 力扣(LeetCode)![]() https://leetcode.cn/problems/linked-list-cycle/142. 环形链表 II - 力扣(LeetCode)
https://leetcode.cn/problems/linked-list-cycle/142. 环形链表 II - 力扣(LeetCode)![]() https://leetcode.cn/problems/linked-list-cycle-ii/
https://leetcode.cn/problems/linked-list-cycle-ii/
第一道题是给我们一个链表Head,让我们判断这是一个带环链表还是一个不带环链表。
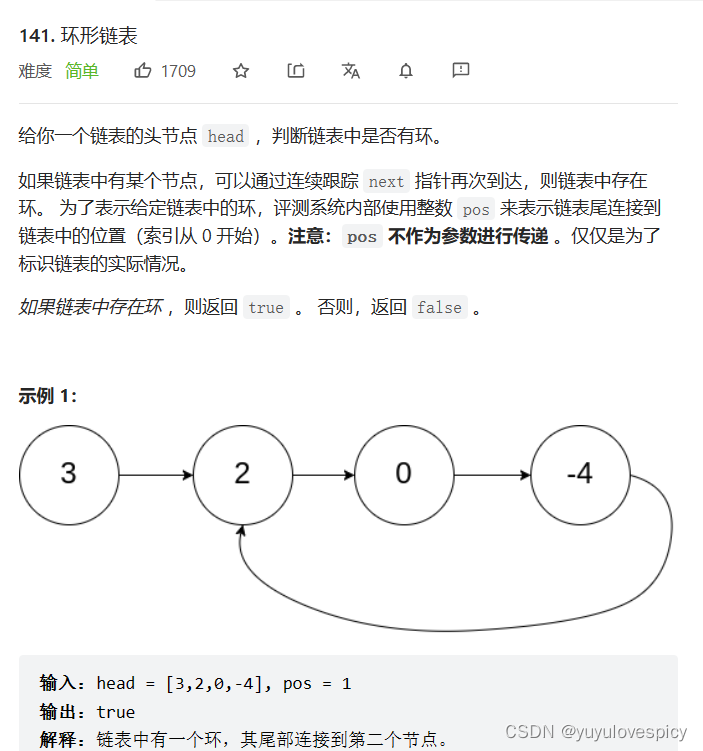
第二个问题是,如果判断出这是一个带环链表,那么请你找出入环点在哪,如下图,开始入环的节点是2这个节点,我们就是要找出2这个入环节点。
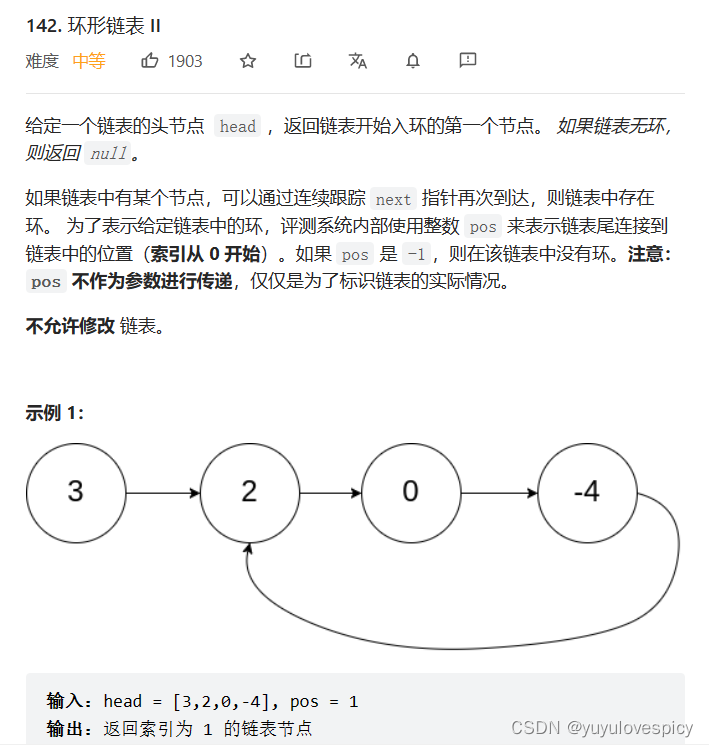
下面我们依次解决这两个问题。

3.判断是否为带环链表
我们如果以cur走到空作为循环的条件,那带环链表就会陷入死循环,这是我们不愿意看到的,那如何才能判断出这是一个带环/不带环链表呢?
带环链表,那肯定是带环的,现实中我们的操场上的400m环形跑道也是环形的,在环形跑道上总会发生一件事情:套圈!!!尤其是现在环形跑道有一个跑得特别快的人和一个跑得特别慢的人,假设他们在进行5000m比赛,如果他们一直跑,跑得特别快的人一定会在某一时刻追上跑得慢的人,然后套跑得慢的人的圈,套圈就意味着某个时刻跑得快的人追上,即和跑得慢的人相遇。而如果是100m比赛,这种没有圈,即没有环的跑道,就不存在套圈,即跑得特别快的人会始终在跑得慢的人前面,直到到达终点,他们永远不会相遇。
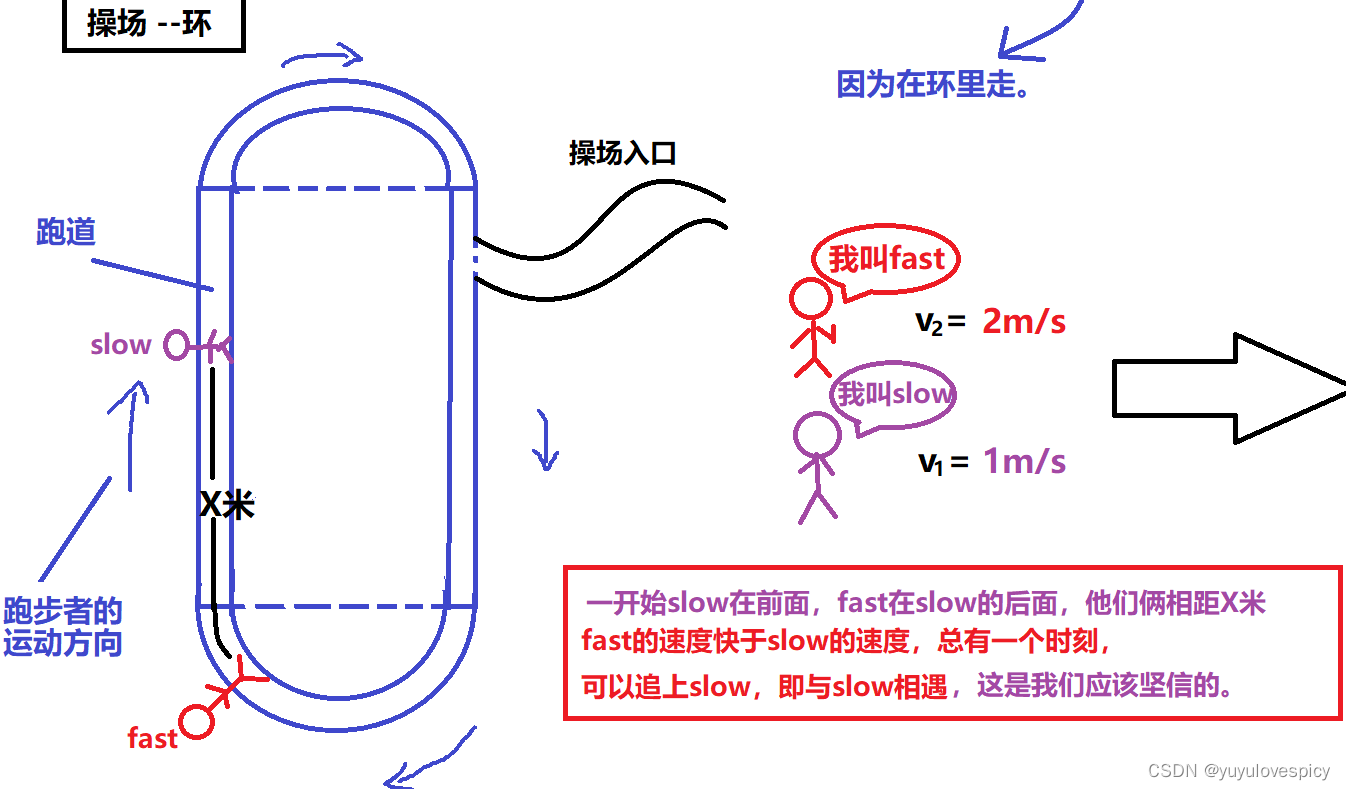
现在我们具象化,现在有两个人fast和slow,fast以2m/s的速度匀速前进,slow以1m/s的速度匀速前进,且现在slow在fast前X米,即fast需要追X米才能追上slow,即fast要比slow多跑X米,才会相遇。如果fast和slow一直在环中跑,fast总有一个时刻可以追slowX米,和slow相遇。
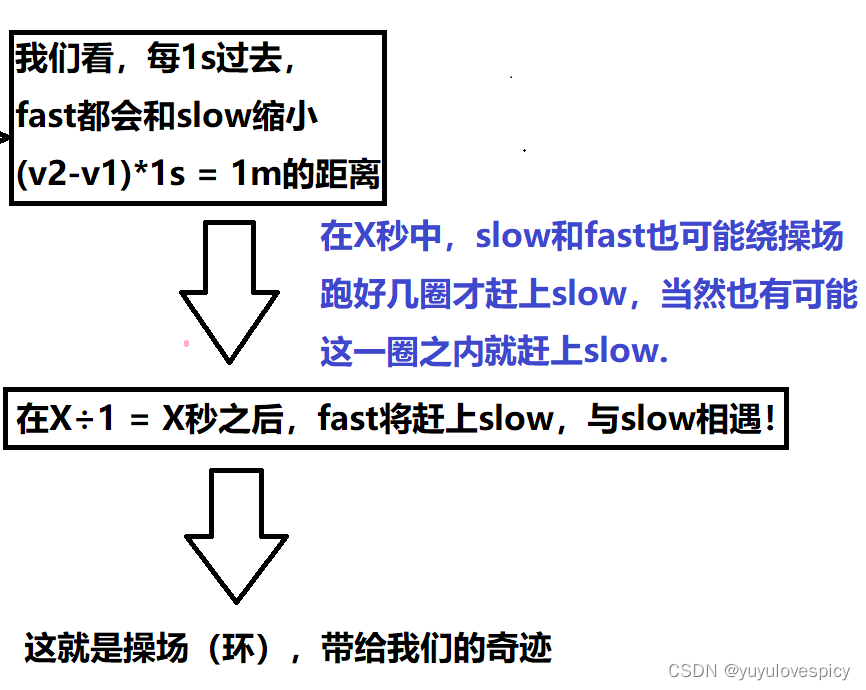
按照这个思路,如果我们定义两个快慢指针fast和slow,他们同时在起点head出发,fast速度是一次走两步fast = fast->next->next,slow的速度是一次走一步slow = slow->next。
如果链表不带环,就是一条线走到底,那fast/fast->next会首先走到尾空NULL,fast和slow永远不会相遇。
而如果链表带环,那fast一定会一马当先入环,然后fast开始在环里转圈圈, 等待slow入环,等slow入环时,fast和slow的环内追击战就开始了!
每fast和slow的走一次,fast和slow就缩小一个节点的距离,若从slow入环的那一刻开始,slow和fast差X节点的距离,slow和fast走X次之后,即fast走2X个节点,slow走X个节点,此时fast和slow追上相遇,即fast==slow。这是带环所必然经历的事情。
bool hasCycle(ListNode *head) {
ListNode* fast = head;
ListNode* slow = head;
//若不带环,fast会一直走到最后一个节点/NULL
while(fast && fast->next)
{
fast = fast->next->next;
slow = slow->next;
//入环之后,fast每次缩小与slow一个节点距离,一定会和slow相遇
if(fast == slow)
{
return true;
}
}
//不带环
return false;
}4. 寻找入环节点(法一:数学推理的魅力)
在第一个问题的基础上,我们引入第二个问题:如果带环,那入环节点在哪呢?
这其实是个数学问题!!!我们先摆出结论:(第一个问题的基础)如果fast和slow从起点head出发,fast一次走两步,slow一次走一步,如果链表带环,那到最后fast和slow一定会在环中的某个节点相遇,这个相遇的节点位置我们记录为meetnode。(第一个问题延伸)然后记录两个节点node1,node2,一个节点从起点head出发,另一个节点从meetnode出发,node1和node2分别都一次走一步,node1和node2一定会相遇,且他们相遇的地方就是入环点!!!!!
ListNode *detectCycle(ListNode *head) {
//判断是否有环
ListNode* fast = head;
ListNode* slow = head;
//无环fast会走完这个链表
while(fast && fast->next)
{
fast = fast->next->next;
slow = slow->next;
//如果带环,fast和slow会在环中某个节点相遇
if(fast==slow)
{
//记录相遇位置为meetnode
ListNode* meetnode = slow;
//node1从meetnode走,node2从head走
ListNode* node1 = meetnode;
ListNode* node2 = head;
//最终node1和node2一定相遇,且相遇点是入环节点
while(node1!=node2)
{
node1 = node1->next;
node2 = node2->next;
}
return node1;
}
}
//无环情况
return nullptr;
}
为什么会这样呢?下面我们证明这个结论:
我们先把fast在环中追到slow的场景塑造出来:
这个带环链表,到达入环点前的要走的直线距离是L个节点,环的长度(环的节点数)为C,slow一次走一步,fast一次走两步,同时从起点head出发。
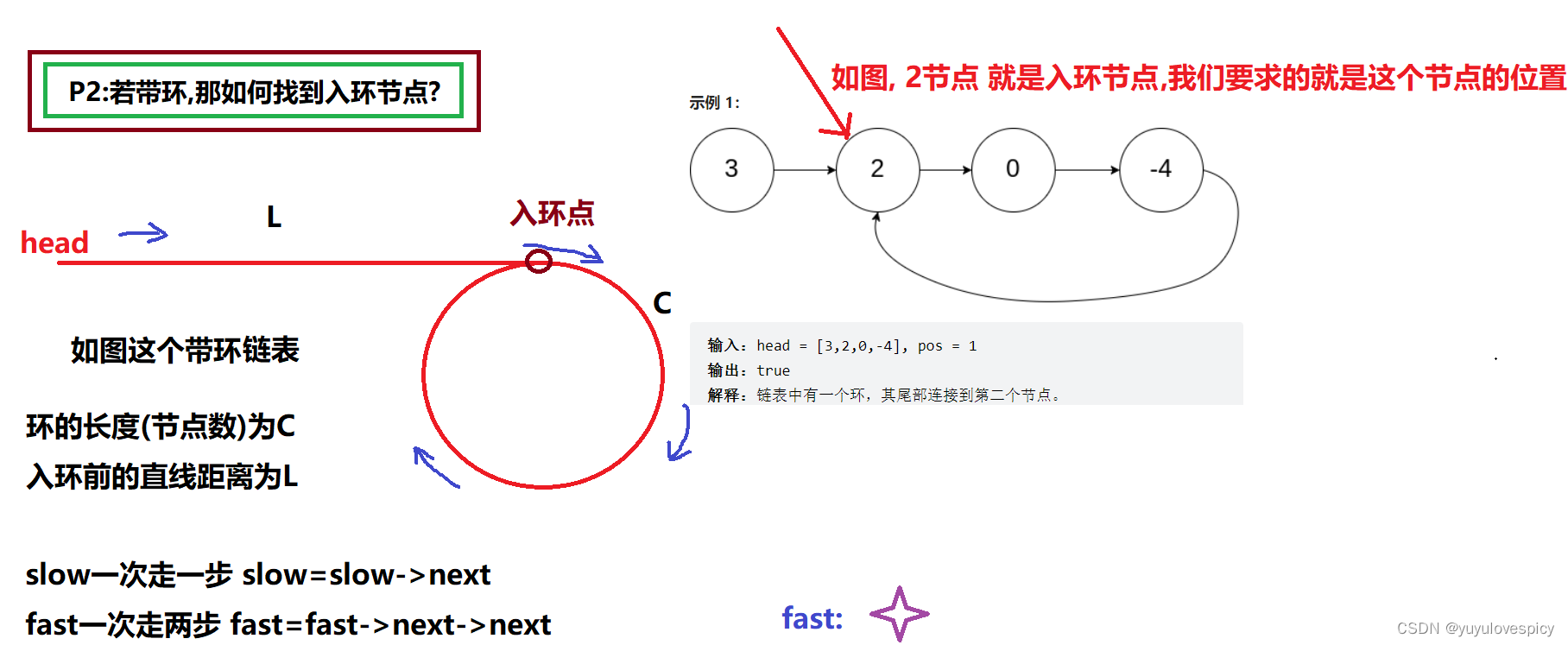
然后一定是fast先入环,slow一次走一步,当slow入环,即slow到达入环点的时候,假设此时fast距离slow有X步,即fast要追slowX步才相遇。
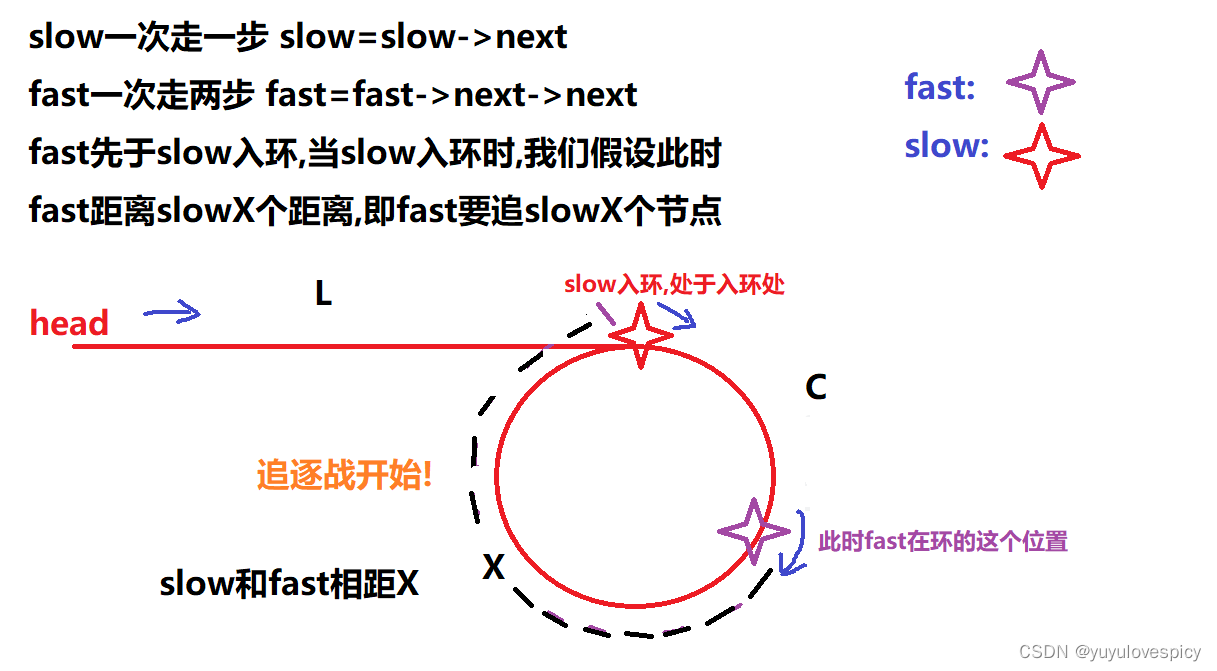
fast的速度是一次两步,slow的速度是一次一步,每次走完fast与slow缩小一步的距离,那走了X次之后,即fast走了2X,slow走了X,2*X - X = X,fast追上slow,与之相遇。然后我们标记相遇点为meetnode。
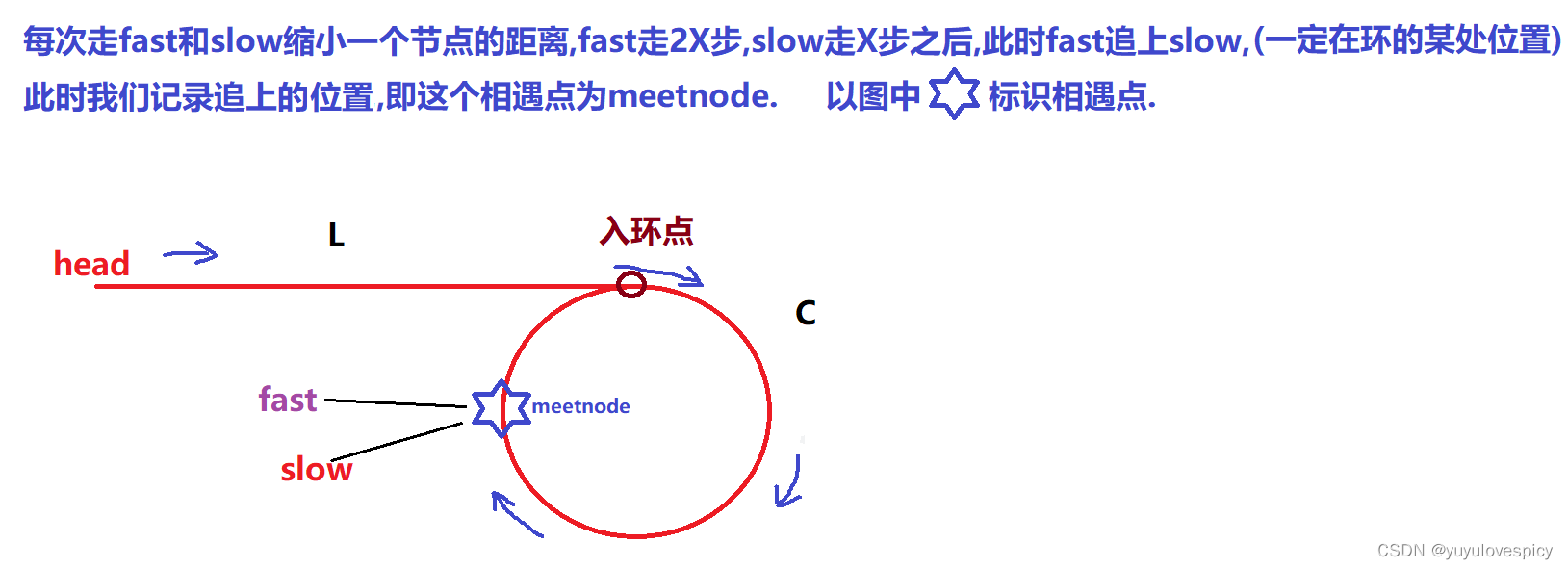
根据结论:我们知道如果此时让node1从meetnode出发,node2从head出发,最后node1和node2一定会相遇,且相遇点就是入环点!!!下面我们根据上面的全过程进行推论:
1.slow和fast一直都在走,slow的速度始终是一步,fast的速度始终是两步,fast速度始终是slow的两倍,所以直至fast和slow在meetnode相遇,fast走过的总距离一定是slow走过的总距离的两倍!
而我们知道slow走了L距离到达入环点,此时fast和slow相距X步,在环中开始fast和slow的追逐战,然后在环中走X次,即fast走2X步,slow走X步后,fast追上slow,即fast和slow在相遇点meetnode相遇。这个全过程slow走了L+X步,fast的速度始终是slow的两倍,所以从这个角度分析fast走的总距离一定是2(L+X)。
2.我们知道fast首先走过L,先于slow入环,然后fast在环中逛游,然后等到slow到达入环点的时候,此时fast和slow相距X步,一圈的步数是X,所以fast所处的位置是距离入环点C-X处,所以在slow到达入环点之前,fast一定是在环内走了C-X步到预定位置的。
可是fast在环内只能走C-X步吗?
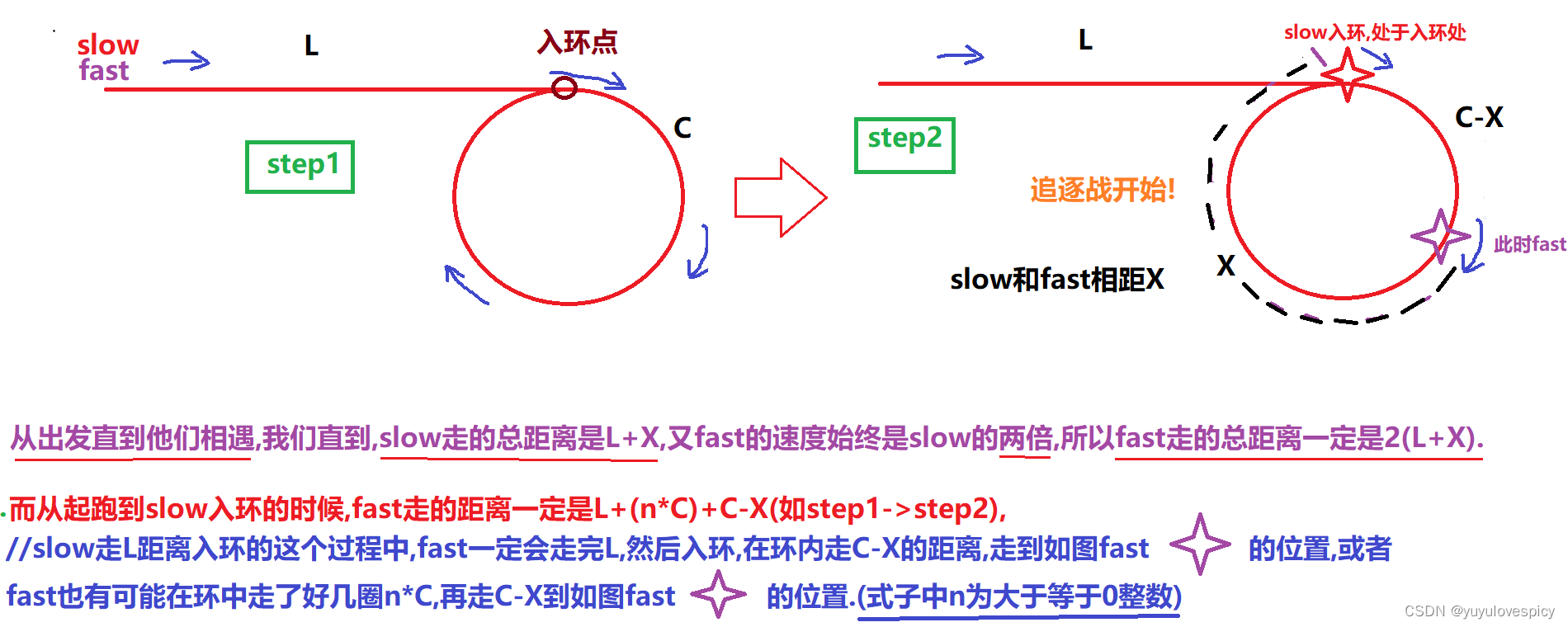
从slow达到入环点之前,在这个过程中,fast不仅是走C-X达到预定位置,有可能fast在到达预定位置之后,fast又在环中走了好多圈,也有可能fast一圈也没走完,可以说slow到达入环点之前fast在环中走了多少几圈,走了多少圈都是不一定的。即在slow达到入环点之前,fast在环内走了有可能走了n*C + C-X(n>=0),这样slow到达入环点的时候,fast所处的位置还是距slowX步的。
所以在slow到达入环点的时候,fast已经走了L + n*C + C-X了,然后slow到达入环点开启追逐战:此时fast和slow相距X,然后fast追了slowX步,即fast走2X步,slow走X步后,两者相遇。
我们总结上述过程fast走的总距离是 L + n*C + C-X + 2X = L + n*C + C + X。(n>=0)
从上面这个角度我们得出fast和slow相遇之前,fast走得总距离是2(L+X),也是(L + n*C + 2X),2L+2X = L + n*C + C + X,所以我们得到 L = n*C + C - X。(n>=0)
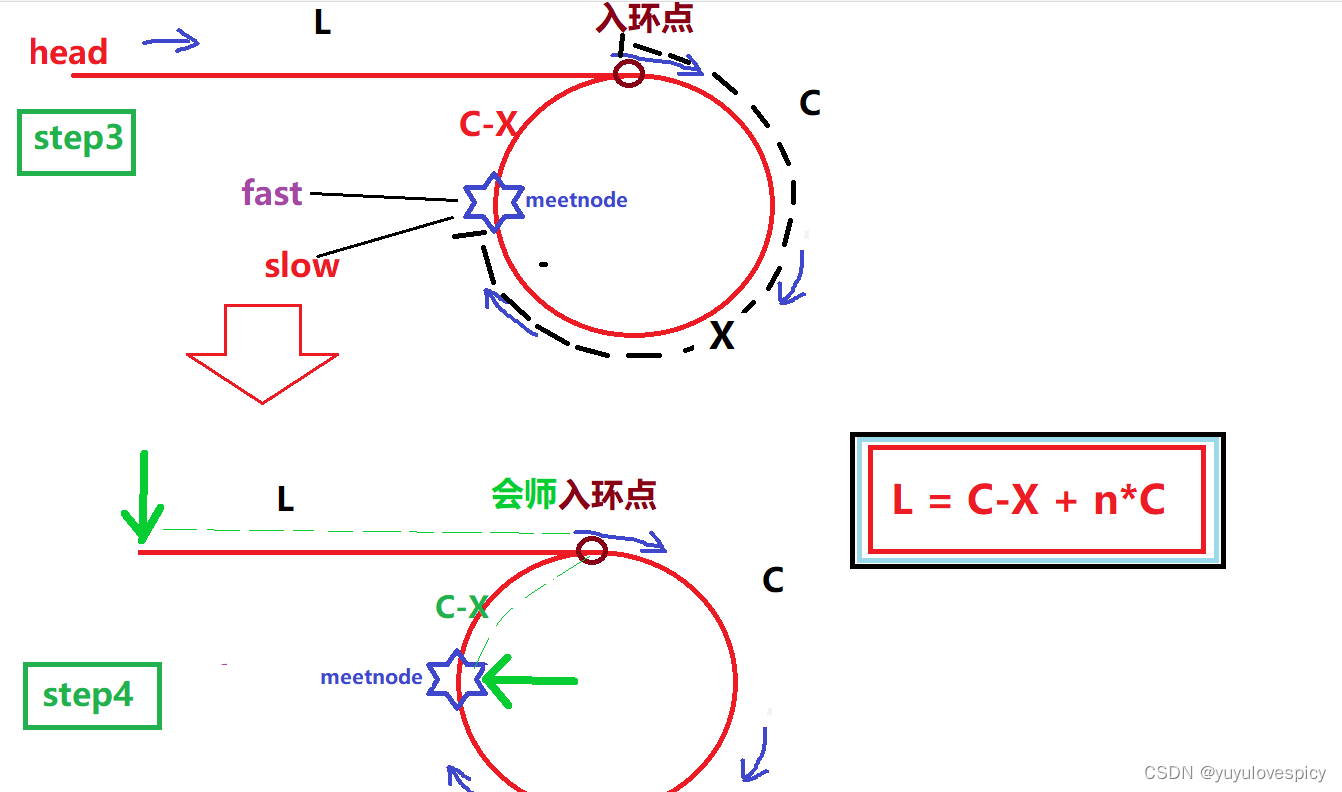
然后让node1从head走,node2从meetnode出发,node2从head走到入环点需要走L步,node1从meetnode出发,在node2走L步到达入环点,node1会走C-X + n*C,即node1也会走C-X步到达入环点,然后走n圈还是在入环点,此时我们可以看到node1和node2一定会在入环点相遇。
所以结论正确:
(第一个问题的基础)如果fast和slow从起点head出发,fast一次走两步,slow一次走一步,如果链表带环,那到最后fast和slow一定会在环中的某个节点相遇,这个相遇的节点位置我们记录为meetnode。(第一个问题延伸)然后记录两个节点node1,node2,一个节点从起点head出发,另一个节点从meetnode出发,node1和node2分别都一次走一步,node1和node2一定会相遇,且他们相遇的地方就是入环点!!!!!
5. 寻找入环节点(暴力拆解带环链表的魄力)
在第一个问题的基础上,fast和slow一定会在环内相遇,记录相遇点为meetnode,然后我们对链表做拆解,把meetnode节点与它的下一个节点newhead做分离,即newhead->next = node改为newhead->next = NULL。完成链表的拆解,带环链表变相交链表。
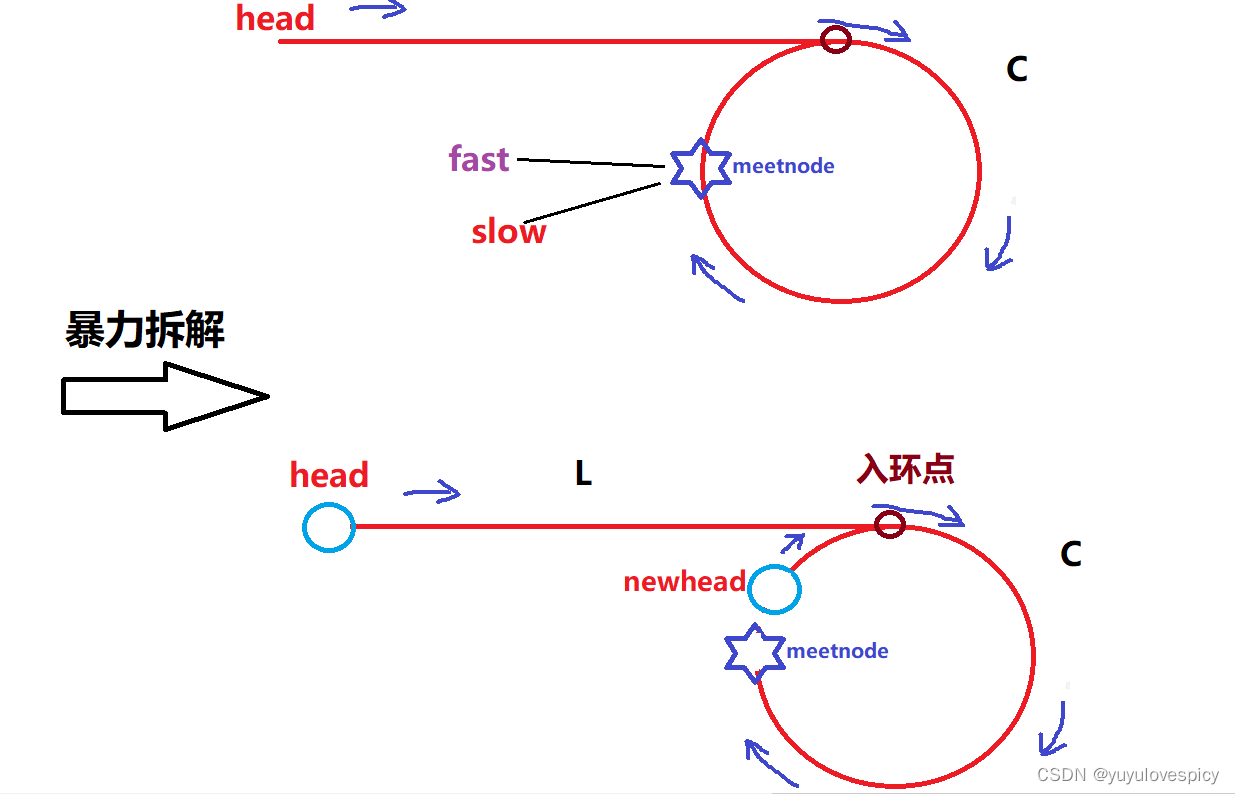
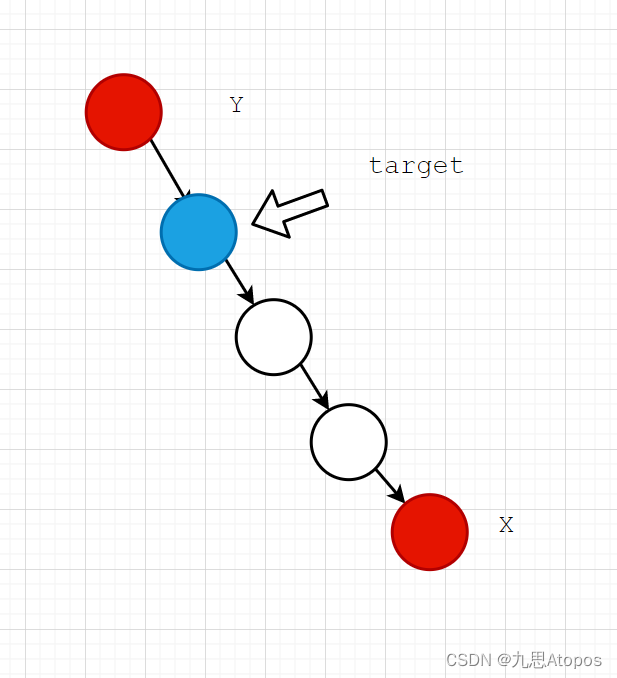
然后这个环形链表就转化为下面这个问题:
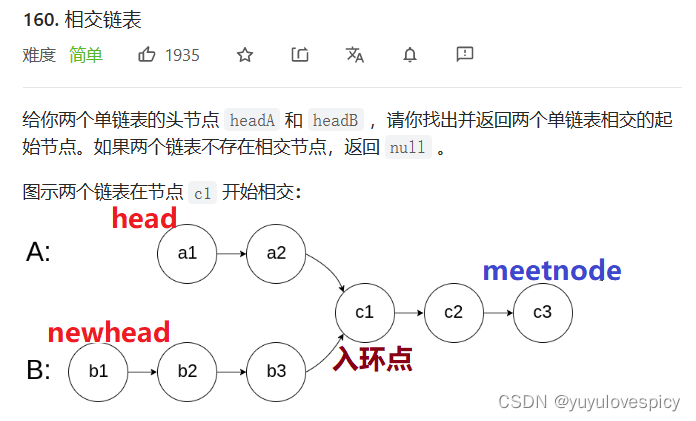
然后就变成了head和newhead两个相交链表,我们只要求得相交链表的第一个相交节点即为入环点的位置。
对于相交链表的思路,可以在我的博客(一网打尽链表的经典OJ题!链表必考笔试题第二弹)中找到,这里我们简述一下思路,先求出分别求出相交链表1和2的长度len1与len2,然后算出差距步abs(len1-len2),然后让较长的相交链表先走差距步,走完差距步之后,两个链表再同时出发,直到他们相等就停下,此时停下的相等的节点的位置就是两个相交链表的起始相交节点,即入环点。
ListNode *detectCycle(ListNode *head) {
//判断是否有环
ListNode* fast = head;
ListNode* slow = head;
//无环fast会走完这个链表
while(fast && fast->next)
{
fast = fast->next->next;
slow = slow->next;
//如果带环,fast和slow会在环中某个节点相遇
if(fast==slow)
{
//记录相遇位置为meetnode
ListNode* meetnode = slow;
ListNode* newhead = meetnode->next;
//把meetnode节点的后一个节点newhead的next置空,拆解链表
meetnode->next = nullptr;
//然后就变成了head和meetnode两个相交链表
//我们只要求得相交链表的第一个相交节点即为相遇点
int len1 = 0,len2 = 0;
ListNode* cur1 = head;
ListNode* cur2 = newhead;
while(cur1)
{
++len1;
cur1 = cur1->next;
}
while(cur2)
{
++len2;
cur2 = cur2->next;
}
int derta_len = abs(len1-len2);
ListNode* longlist = head;
ListNode* shortlist = newhead;
if(len1<len2)
{
longlist = newhead;
shortlist = head;
}
while(derta_len--)
{
longlist = longlist->next;
}
while(longlist!=shortlist)
{
longlist = longlist->next;
shortlist = shortlist->next;
}
return longlist;
}
}
//无环情况
return nullptr;
}6.番外:判断是否为带环链表(fast和slow的速度选择)
判断链表是否带环&&如果带环求出入环点位置,这两个问题我们已经得到实质的解决,可是秉承着一颗探索的心,最后我们回到第一个问题。
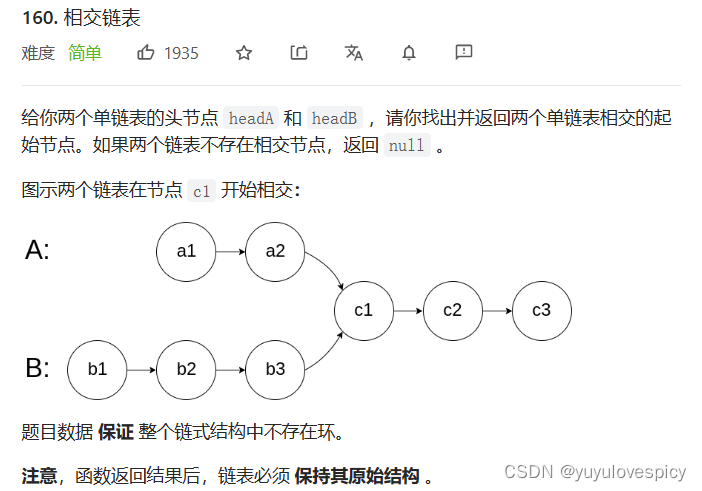
如果fast的速度取每次两步,slow的速度取每次一步,我们先假设slow到入环点的时候,fast距离slow是X步,那么在这个场景下,fast和slow是一定可以相遇,因为每次fast和slow的速度差是每次1步,也就是说,X可以整除1,走X次之后就可以一定可以相遇。
那如果fast的速度不是每次两步,而是每次三步,每次四步,甚至每次五步,在环内fast和slow还一定能相遇吗?会不会遇到这种情况:fast可以追上超过slow,却永远不能与slow相遇。当然是有可能的!我们随便举一个例子你就懂了:
若环的长度C=2,当slow到达入环点的时候,fast和slow差1步,即起始fast和slow的差距为X=1。
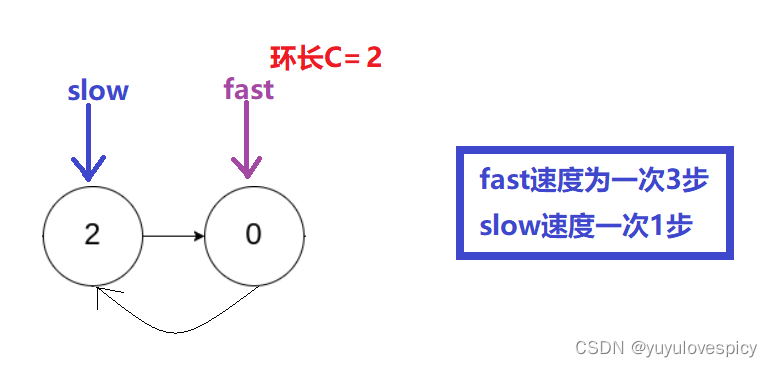
在这种情况下,fast和slow是永远不能相遇的,为什么这么说:fast和slow速度差是3-1=2,即每次两步,即每次走完fast能比slow多走2步。运用高中物理运动学的知识,我们可以采用参考系相对静止的方法,让slow静止,fast以每次2步的在走,此时fast和slow相遇,与fast走每次3步,slow每次1步是等效的。这是第一个我们要使用的技巧。同时我们也可以看到fast能否和slow相遇,看的并不是fast和slow的绝对速度,而是fast和slow的相对速度差!
我们现在在参考系相对静止的场景下,让slow静止,fast以相对速度差前进:能否相遇看的就是能不能让fast走到slow的位置,那fast如何才能走到slow的位置呢,最简单的当然是fast正好走X步到达slow所在的位置,但是fast的相对速度差,即每次2步,不一定可以整除X,如果X是奇数,即如图X==1,即很有可能fast无法正好一步到位slow,而跑到slow的前一个位置。如上面一个例子,slow静止,fast每次两步,fast每次走完都会回到原位,永远不可能与slow相遇!!!而如果fast的速度取每次两步,slow的速度取每次一步,即相对速度差是1时,那相遇就是板上钉钉的事情了。那为什么相对速度差是非1(如上例是2)的时候,有可能遇到fast和slow永远无法相遇的情况呢?
我们仍然以相对速度差为2举例,做出如下具体分析:
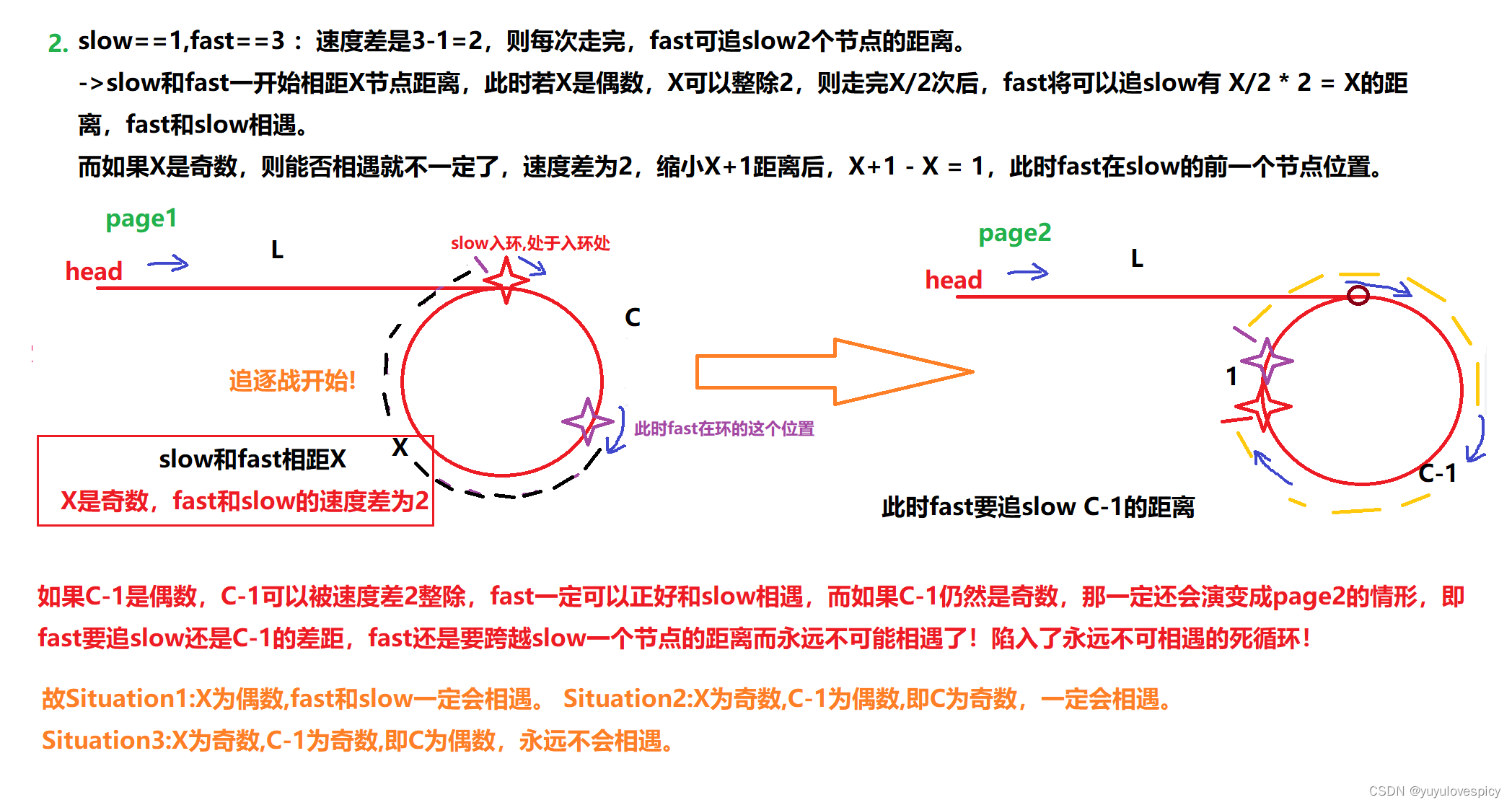
如果相对速度差为3,从这个例子我们推而广之,那fast和slow能否相遇的命题就是这样的:
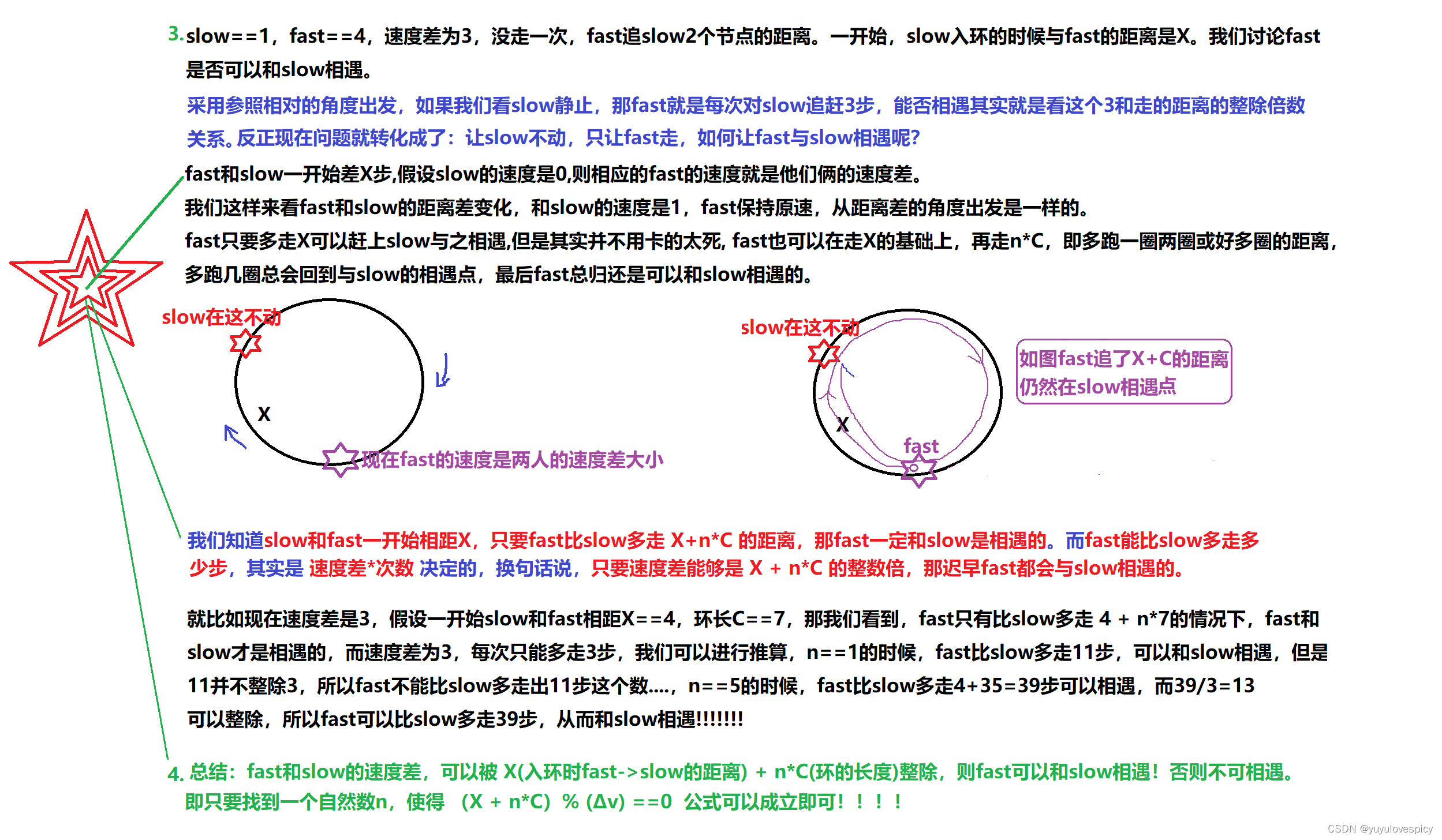
![[GXYCTF2019]BabysqliV3.0](https://img-blog.csdnimg.cn/b65c232e6f3e4b169994eefa6b42bee2.png)