$AC$来的如此之快，让我以为还要再调试几个点(h)，本文涉及思路参考：参考文章
嗯,这个题和思路让我对跨父节点的树上链有了一个认识，我们来看一下：

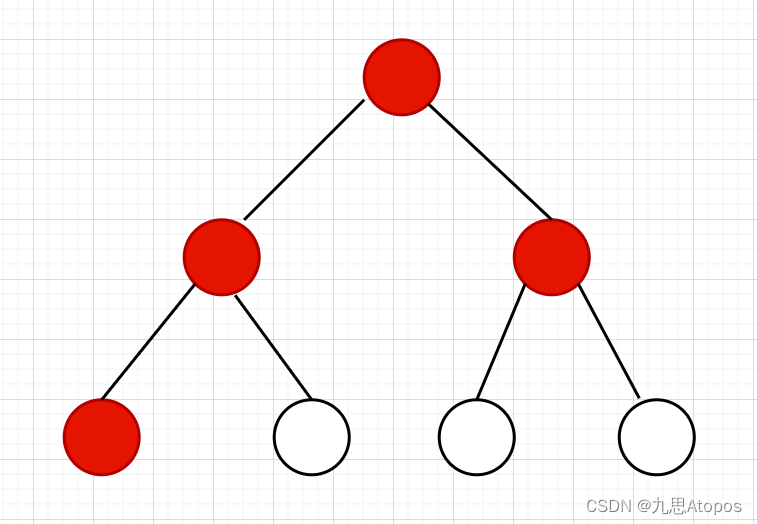
如果说，我们要对这样的一条链进行$dp$操作，该怎么弄呢？我们需要的是求公共祖先（可以参考我曾经写过的LCA）的思路：

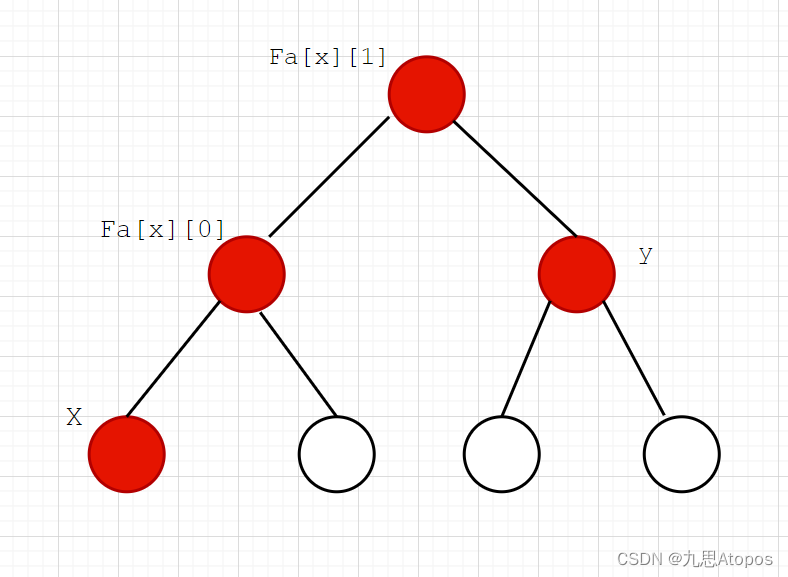
这样是不是就明白了？有人可能会问，那如果$x$和$y$在一条链上，你还咋用？换个说法，如果$x$和$y$形如下图：

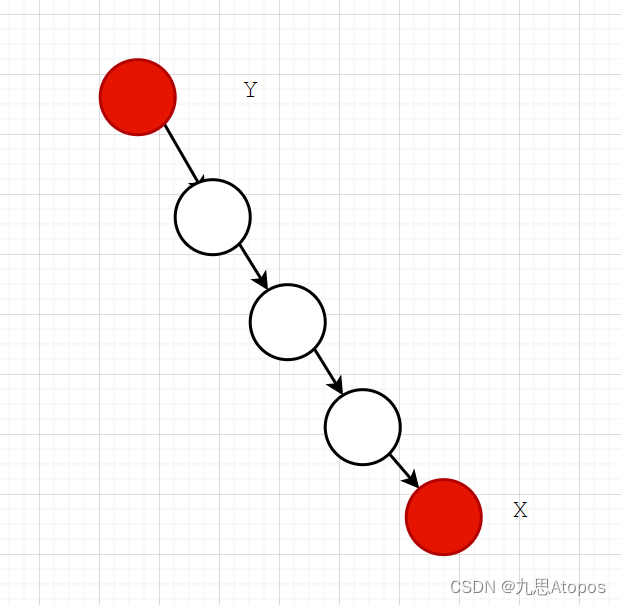
而我想要找到距离$y$最近的$x$的祖先，也就是：

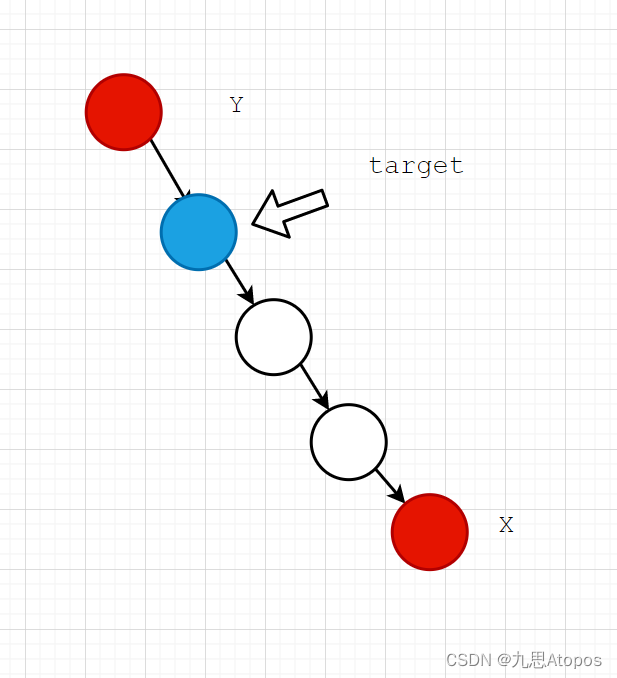
应该怎么求呢？这个时候就可以利用$x$来求，还记得我们在求公共祖先的时候，让$x$和$y$到达同一个高度的代码吗？

while(dep[x]!=dep[y])
{
    x=fa[x][lg[dep[x]-dep[y]]-1];
 }

那我们这里就可以看成是让$x$和$target$到达同一个高度上，所以可以把上面的代码改写成：

while(dep[x]!=dep[y]-1)
{
    x=fa[x][lg[dep[x]-dep[y]-1]-1];
}

通过$x$求得$target$，这就是$LCA$应用在树形$dp$上的方法；至于本题的状态方程可以写成为：

dp[l][r]=max(dp[l][r-1],max(dp[l+1][r],
            dp[l+1][r-1]+(p[l]==p[r])?2:0));

后记：勤把自己做过的题记录下来还是有好处的，至少在以后啥也不会的时候还能看看…
AC代码：

#include<iostream>
#include<cstdio>
#include<vector>
#include<cmath>
#include<algorithm>
using namespace std;
const int length = 2100;
int fa[length][length];
int lg[length];
int dep[length];
int vis[length];
int dp[length][length];
void dfs(int cur, vector<vector<int>> &edge, int father)
{
	for (int v : edge[cur])
	{
		if (vis[v] == 0 && v != father)
		{
			vis[v] = 1;
			fa[v][0] = cur;
			dep[v] = dep[cur] + 1;
			for (int i = 1; i < dep[v]; i++)
			{
				fa[v][i] = fa[fa[v][i - 1]][i - 1];
			}
			dfs(v,edge,cur);
			vis[v] = 0;
		}
	}
}
int LCA(int x, int y)
{
	//先把x和y提到一个高度上，然后x和y一起往上跳
	//首先让x的高度大于y
	if (dep[x] < dep[y])
	{
		swap(x, y);
	}
	while (dep[x] != dep[y])
		x = fa[x][lg[dep[x] - dep[y]] - 1];
	if (x == y)return x;//他俩重合在一起了
	for (int i = lg[dep[x]] - 1; i >= 0; i--)
	{
		if (fa[x][i] != fa[y][i])
		{
			x = fa[x][i];
			y = fa[y][i];
		}
	}
	return fa[x][0];
}
int DP(int x, int y,char *p)
{
	if (dp[x][y] != 0)
		return dp[x][y];
	int delta = 0;
	if (p[x] == p[y])
	{
		delta = 2;
	}
	else delta = 0;
	if (dep[x] < dep[y])
	{
		swap(x, y);
	}
	int lca = LCA(x, y);
	if (y == lca)
	{
		//首先找到离y最近的x的祖先节点
		int tmp = x;
		while (dep[y] != dep[x] - 1)
		{
			x = fa[x][lg[dep[x] - dep[y] - 1] - 1];
		}
		swap(tmp, x);
		dp[y][x]=dp[x][y]=max(DP(fa[x][0], y, p), max(DP(tmp, x, p), DP(tmp, fa[x][0], p)+delta));
		return dp[x][y];
	}
	else
	{
		dp[y][x]=dp[x][y]=max(DP(fa[x][0], y,p), max(DP(x, fa[y][0],p), DP(fa[x][0], fa[y][0],p) + delta));
		return dp[x][y];
	}
}
int solve(char *p,int n)
{
	//先给dp数组做初始化
	for (int i = 1; i <= n; i++)
	{
		int yh = fa[i][0];
		if (p[i] == p[yh])
		{
			dp[i][yh] = 2;
			dp[yh][i] = 2;
		}
		else
		{
			dp[i][yh] = 1;
			dp[yh][i] = 1;
		}
		dp[i][i] = 1;
	}
	//然后进行树上的链DP
	int ans = -1;
	for (int i = 1; i <= n; i++)
	{
		for (int j = 1; j <= n; j++)
		{
			ans = max(ans, DP(i, j,p));
		}
	}
	return ans;
}
int main(void)
{
	int t;
	scanf_s("%d", &t);
	for (int i = 1; i < length; i++)
	{
		lg[i] = lg[i - 1] + ((1 << lg[i - 1]) == i ? 1 : 0);
	}
	for (int i = 0; i < t; i++)
	{
		memset(fa, 0, sizeof(fa));
		memset(dp, 0, sizeof(dp));
		memset(dep, 0, sizeof(dep));
		int n;
		scanf_s("%d", &n);
		char p[length];
		scanf_s("%s", &p[1], sizeof(p));
		vector<vector<int>> edge(length);
		for (int i = 0; i < n - 1; i++)
		{
			int a, b;
			scanf_s("%d%d", &a, &b);
			edge[a].push_back(b);
			edge[b].push_back(a);
		}
		vis[1] = 1;
		dfs(1, edge, -1);
		int ans=solve(p,n);
		printf("%d\n", ans);
	}
}