目录

KMP

字符串哈希

最长回文子串

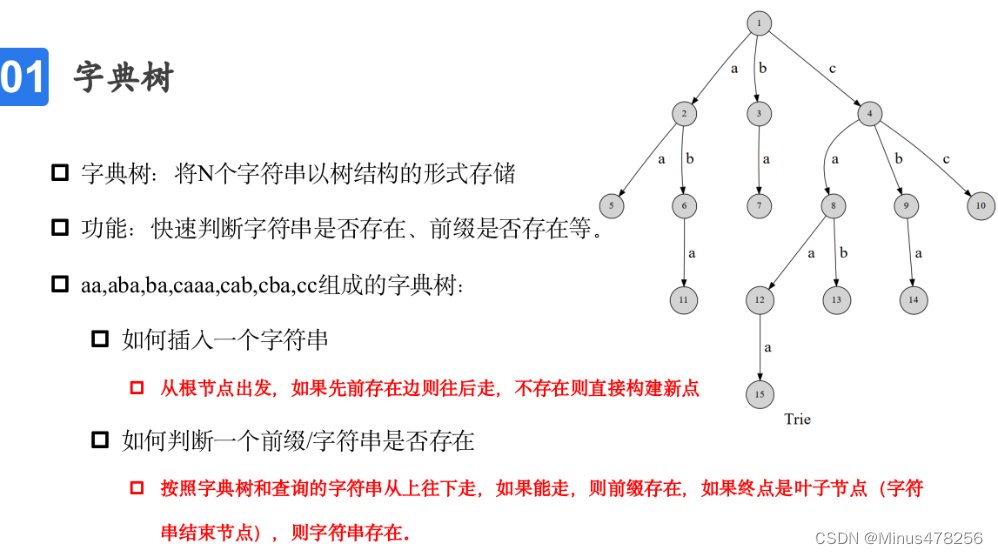
字典树

---

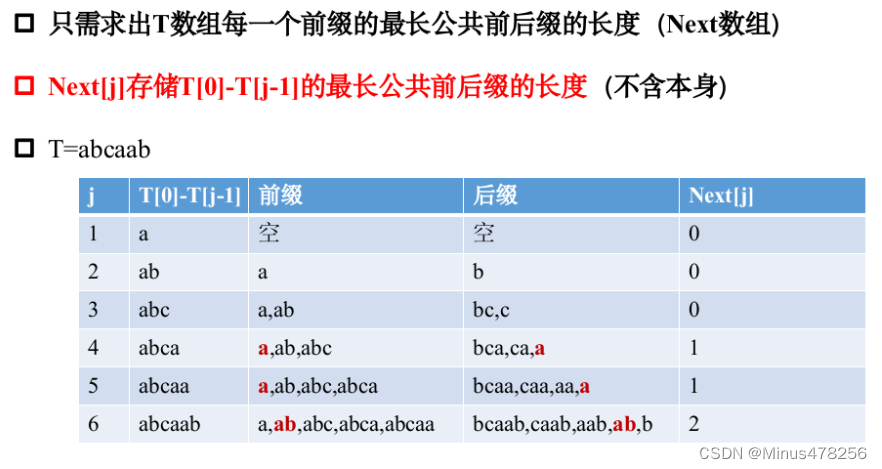
KMP

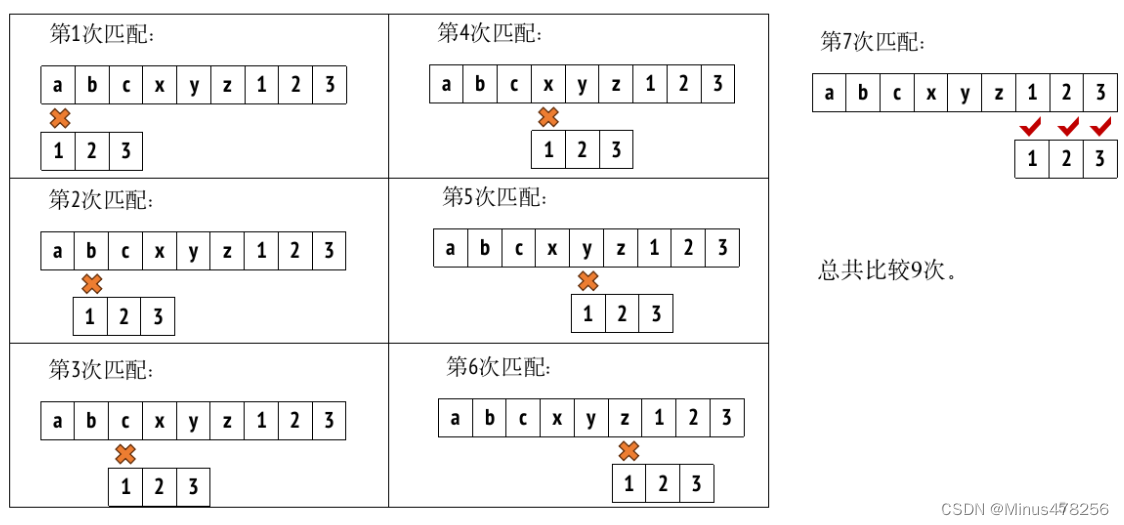
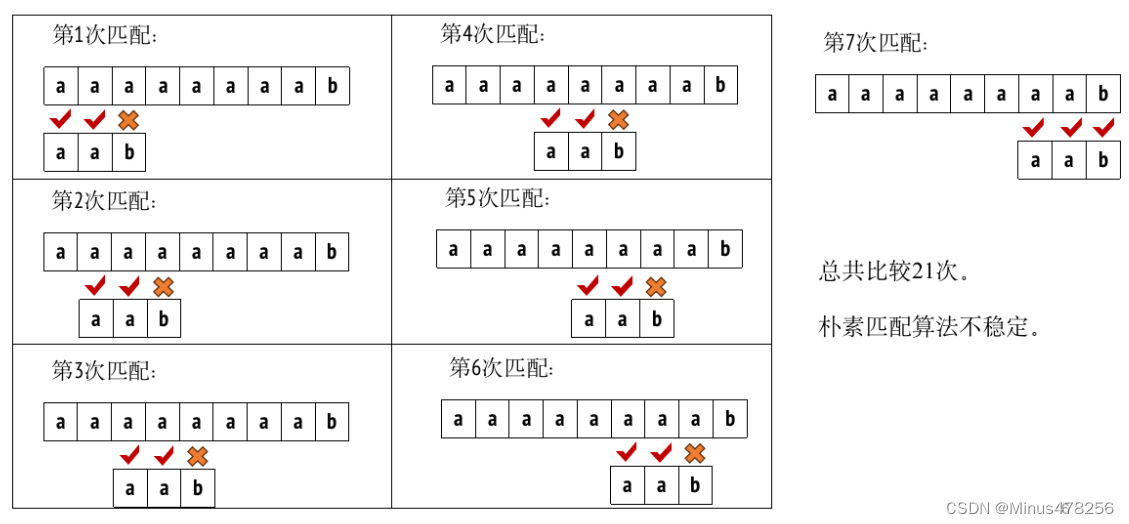
模式匹配问题：

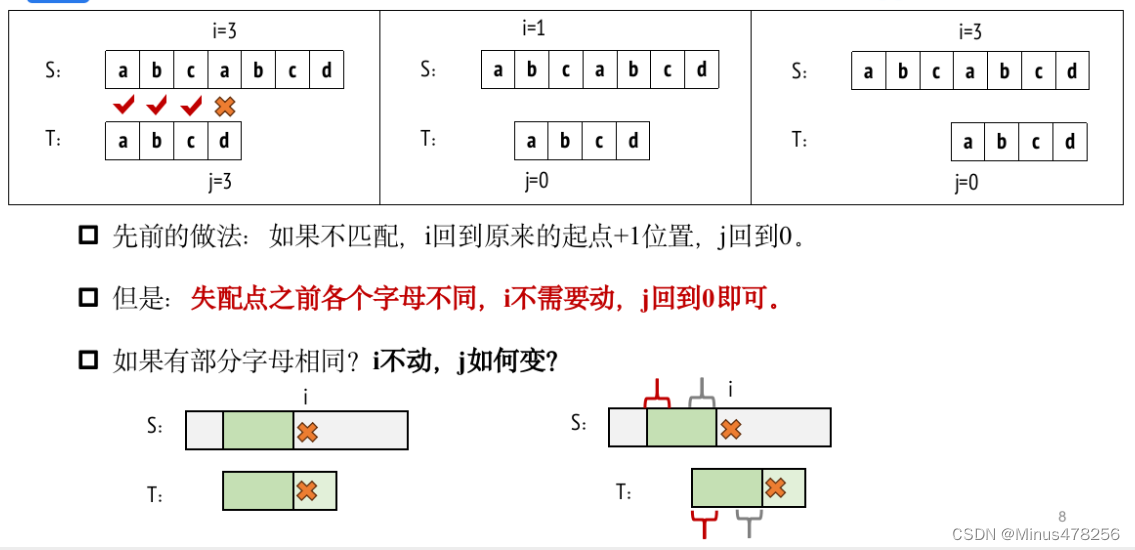
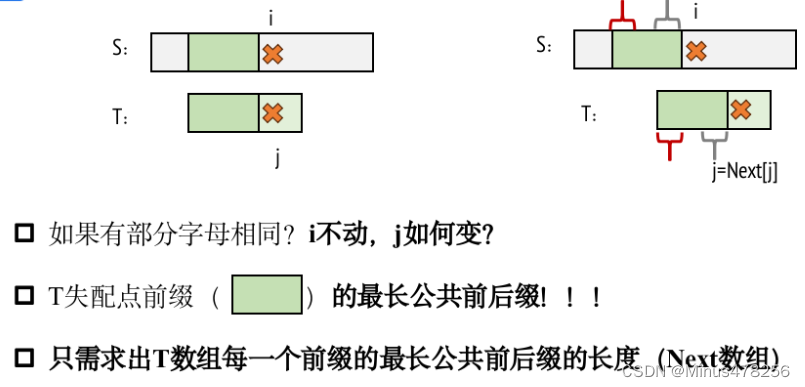
KMP算法：

用动规的思想求Next数组：如果后缀的i位置==前缀的j位置，Next[i+1]=j+1；如果后缀的i位置!=前缀的j位置，那就用KMP算法，令j=Next[j]

#母串S，模式串T
Next=[0]*1000010
#1.求模式串T的Next数组
def get_next(T):
    #求1Next[i]，利用Next[0,...,i-1]
    for i in range(1,len(T)):
        j=Next[i]
        #不断地往前找到能够匹配的j
        while j>0 and T[i]!=T[j]:# 走到头或相等则停下
            j=Next[j]
        if T[i]==T[j]:
            Next[i+1]=j+1
        # j已经走到0的位置了，但是还没有匹配，则在i+1处的位置的Next应设为0
        else:
            Next[i+1]=0
#返回字符串s中t出现的次数
def KMP(s,t):
    get_next(t)
    ans=0
    j=0
    for i in range(len(s)):
        while j>0 and s[i]!=t[j]:
            j=Next[j]
        #判断是否匹配
        if s[i]==t[j]:
            j+=1
        #判断是否匹配完成
        if j==len(t):
            ans+=1
            #二次匹配，直到i遍历s
            j=Next[j]
    return ans

t=input()
s=input()
KMP(s,t)

字符串哈希

最长回文子串

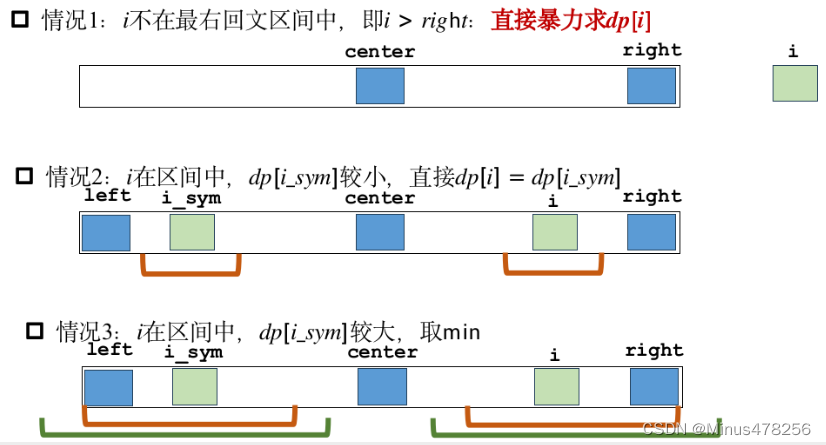
马拉车算法

当遇到偶数字符串时，在每个字符之间添加分隔符，就能保证字符长度又为奇数了。所以只要会处理奇数字符串是否回文的问题就好。

#s从左端点l和右端点r向两端扩展，
# 返回可扩展的长度
def expend(s,l,r):
    #保证s[l]==s[r]即可
    while l>=0 and r<len(s) and s[l]==s[r]:
        l-=1
        r+=1
    #最终返回
    #当循环结束时，l和r所在位置不满足条件了
    #因此满足条件的范围是：(r-1)-(l+1)
    return (r-l-2)//2

#求最长回文子串
def longest(s):
    s='#'+'#'.join(list(s))+'#'
    #构建dp数组
    dp=[0]*len(s)
    #维护最右端的回文子串
    center,right=0,0
    #求dp[i]
    for i in range(1,len(s)):
        if i>right:
            dp[i]=expend(s,i,i)
        else:
            #对称点
            i_sym=center*2-i
            #当前能利用的最长回文区间
            min_len=min(dp[i_sym],right-i)
            dp[i]=expend(s,i-min_len,i+min_len)
        if i+dp[i]>right:
            center=i
            right=i+dp[i]
    print(s)
    print(dp)
    return max(dp)

#输入s
s=input()
print(longest(s))

字典树