小小总结之二分查找三种情况

news2024/11/20 23:34:13

小小总结之二分查找三种情况

二分查找主要难点在于：

起始条件 left,right的取值，一般若闭合区间，则0, length(nums)。如果涉及边界位置代入计算，则0,length(nums)。
循环条件，第一要能够避免死循环，第二要看保留值（保留边界）问题，left <= right 无值保留，left < right则会剩下left = right一个位置，如果left + 1 < right 则会剩下left, right (right = left + 1)两个位置。
向左向右查找区间：如果是需要保留当前mid作为边界则赋值为mid，否则相应进行+1、-1操作；另外注意避免死循环问题即可，根据具体来定是否进行+1、-1操作。

First：

原题链接：

704. 二分查找 - 力扣（LeetCode）

int search(int* nums, int numsSize, int target) {
    int left = 0, right = numsSize - 1;
    while (left <= right) {
        int mid = left + ((right - left) >> 1);
        if (nums[mid] == target) {
            while (mid > 0 && nums[mid-1] == target) {
                mid--;
            }
            return mid;
        } else if (nums[mid] > target) {
            right = mid - 1;
        } else {
            left = mid + 1;
        }
    }
    return -1;
}

简单的题，题目直接告诉二分查找，并且让搜索是否存在固定值，即：等于x的下标这一情况，直接经典模板，三种比较结果分开列。

边界问题：在查找到目标值时，我们需要进行简单的处理：目标值是否重复？如果不确定的情况下，我们就需要进行查找：

        if (nums[mid] == target) {
            while (mid > 0 && nums[mid-1] == target) {
                mid--;
            }
            return mid;

while循环的条件设置为：边界+判断数组的值是否与目标相同，内部为下标左移或右移，当查找到了，就return下标的值即可。

Second：

原题链接：

35. 搜索插入位置 - 力扣（LeetCode）

int searchInsert(int* nums, int numsSize, int target) {
    int left=0,right=numsSize-1;
    int ans=numsSize;
    while(left<=right){
        int mid=left+((right-left)>>1);
        if(nums[mid]<target){
            left=mid+1;
        }
        else {
            ans=mid;
            right=mid-1;
        }
    }
    return ans;
}

返回按顺序插入的位置，即：大于等于x的最小下标。

我们这个时候就可以想想，

当左边界收缩的时候，对我们的结果有影响吗？

没有，因为我们要求的是最大的下标，那么我们只有在右边界收缩的时候才会影响我们的结果，

所以我们的用一个答案变量保存一下我们的mid，再进行收缩，

那么当右边界收缩的时候，mid的结果大于目标，所以就保证了这个数据一定大于等于我们目标值，插入的时候就需要插入到这里。我们返回答案变量即可。

为什么继续查找分别left需要+1,而right不再-1

从起始条件可以看出，每次二分查找的区间为[left, right)，即区间左闭右开。
因此在target与nums[mid]进行比较时，左侧区间和右侧区间分别改变为了[left, mid)和[mid + 1, right)，同样是确保每次mid处的元素不会重复拿出来进行比较（防止死循环）。

Third：

原题链接：

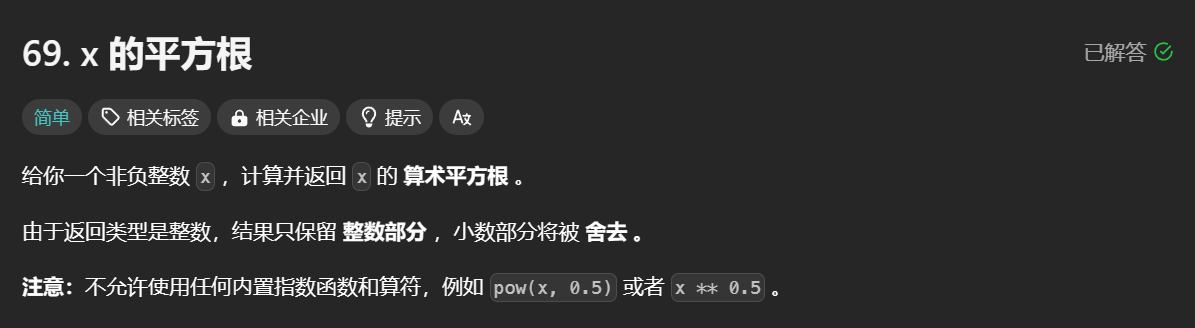
69. x 的平方根 - 力扣（LeetCode）

int mySqrt(int x) {
    long long left = 0, right = 10000000;
    long long ans = 0;
    while (left <= right) {
        long long mid = left + ((right - left) >> 1);
        if (mid * mid <= x) {
            ans = mid;
            left = mid + 1;
        } else {
            right = mid - 1;
        }
    }
    return (int)ans;
}

这里需要我们理解一下，找平方根，并且保留整数部分，什么意思呢，也就是结果必定小于等于真实的情况，也就是：小于等于x的最大下标。

我们在这里，返回的是平方根，所以我们直接让mid的积<=x就可以啦，我们回顾一下上一题，也就是说我们需要返回的是左边界的收缩前的结果。

Fourth：

原题链接：

367. 有效的完全平方数 - 力扣（LeetCode）

bool isPerfectSquare(int num) {
    long long left=0,right=num;
    while(left<=right){
        long long mid=left+((right-left)>>1);
        if(mid*mid<num){
            left=mid+1;
        }
        else if(mid*mid>num){
            right=mid-1;
        }
        else return 1;
    }
    return 0;
}