红黑树平衡艺术:最大化与最小化红色结点比值的策略与实现
- 一、 最大比值的红黑树构造
- 1.1 伪代码示例:
- 1.2 C代码示例:
- 三、最小比值的红黑树构造
- 3.1 伪代码示例:
- 3.2 C代码示例:
- 四、结论
红黑树是一种自平衡的二叉搜索树,它通过一系列的规则和旋转操作来保持树的平衡,从而确保基本动态集合操作的时间复杂度为O(log n)。在红黑树中,每个结点都被标记为红色或黑色,这些颜色的使用是为了保持树的平衡性质。本文将探讨如何构造一棵含有n个关键字的红黑树,使得红色内部结点个数与黑色内部结点个数的比值达到最大和最小,并提供相应的伪代码及C代码示例。
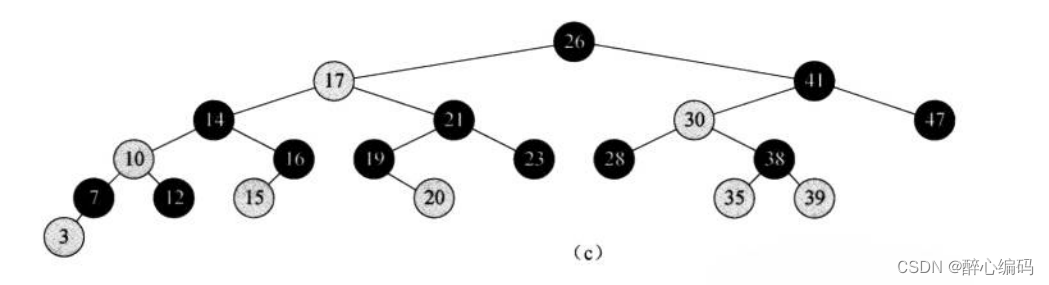
一、 最大比值的红黑树构造
为了最大化红色结点与黑色结点的比值,我们需要尽可能多地使用红色结点,同时不违反红黑树的性质。根据红黑树的性质,我们知道:
- 每个结点要么是红色,要么是黑色。
- 根结点和所有叶子结点(NIL结点)都是黑色的。
- 红色结点的两个子结点都是黑色的。
- 从根结点到每个叶子结点的所有路径上,黑色结点的数量是相同的。
基于这些性质,我们可以通过以下策略来构造树:
- 根结点为黑色。
- 每个黑色结点的子结点交替为红色和黑色,以保持性质3。
- 为了最大化红色结点的数量,我们可以在每个黑色结点下尽可能多地添加红色子结点。
1.1 伪代码示例:
FUNCTION constructMaxRedTree(n)
tree = NEW_TREE
root = NEW_NODE
root.color = BLACK
root.key = 0
root.left = NIL
root.right = NIL
tree.root = root
FOR i FROM 1 TO n
current = tree.root
WHILE current IS NOT NIL
if i % 2 == 1 THEN // 奇数位置插入红色结点
newNode = NEW_NODE
newNode.color = RED
newNode.key = i
newNode.left = NIL
newNode.right = NIL
IF current.key < i THEN
current.right = newNode
ELSE
current.left = newNode
ENDIF
current = current.right
ELSE // 偶数位置插入黑色结点
newNode = NEW_NODE
newNode.color = BLACK
newNode.key = i
newNode.left = NIL
newNode.right = NIL
IF current.key < i THEN
current.right = newNode
ELSE
current.left = newNode
ENDIF
current = current.left
ENDIF
ENDWHILE
ENDFOR
RETURN tree
ENDFUNCTION
1.2 C代码示例:
#include <stdio.h>
#include <stdlib.h>
typedef enum {RED, BLACK} Color;
typedef struct Node {
int key;
Color color;
struct Node *left;
struct Node *right;
struct Node *parent;
} Node;
Node *constructMaxRedTree(int n) {
Node *tree = (Node *)malloc(sizeof(Node));
Node *root = tree;
root->color = BLACK;
root->key = 0;
root->left = NULL;
root->right = NULL;
root->parent = NULL;
for (int i = 1; i <= n; i++) {
Node *current = root;
while (current != NULL) {
if (i % 2 == 1) { // 插入红色结点
Node *newNode = (Node *)malloc(sizeof(Node));
newNode->color = RED;
newNode->key = i;
newNode->left = NULL;
newNode->right = NULL;
newNode->parent = current;
if (current->key < i) {
current->right = newNode;
} else {
current->left = newNode;
}
current = current->right;
} else { // 插入黑色结点
Node *newNode = (Node *)malloc(sizeof(Node));
newNode->color = BLACK;
newNode->key = i;
newNode->left = NULL;
newNode->right = NULL;
newNode->parent = current;
if (current->key < i) {
current->right = newNode;
} else {
current->left = newNode;
}
current = current->left;
}
}
}
return tree;
}
三、最小比值的红黑树构造
为了最小化红色结点与黑色结点的比值,我们应该尽可能多地使用黑色结点。在这种情况下,我们可以构造一棵完全平衡的二叉树,其中每个结点都是黑色的。
3.1 伪代码示例:
FUNCTION constructMinRedTree(n)
tree = NEW_TREE
root = NEW_NODE
root.color = BLACK
root.key = 0
root.left = NIL
root.right = NIL
tree.root = root
FOR i FROM 1 TO n
current = tree.root
WHILE current IS NOT NIL
IF current.key < i THEN
newNode = NEW_NODE
newNode.color = BLACK
newNode.key = i
newNode.left = NIL
newNode.right = NIL
newNode.parent = current
current.right = newNode
current = current.right
ELSE
newNode = NEW_NODE
newNode.color = BLACK
newNode.key = i
newNode.left = NIL
newNode.right = NIL
newNode.parent = current
current.left = newNode
current = current.left
ENDIF
ENDWHILE
ENDFOR
RETURN tree
ENDFUNCTION
3.2 C代码示例:
Node *constructMinRedTree(int n) {
// ... (与前一个函数相同的初始化代码)
// 构造完全平衡的二叉树,每个结点都是黑色
for (int i = 1; i <= n; i++) {
Node *newNode = (Node *)malloc(sizeof(Node));
newNode->color = BLACK;
newNode->key = i;
newNode->left = NULL;
newNode->right = NULL;
newNode->parent = current;
if (i % 2 == 0) { // 插入到左子树
current->left = newNode;
current = current->left;
} else { // 插入到右子树
current->right = newNode;
current = current->right;
}
}
return tree;
}
四、结论
通过上述构造方法,我们可以得出结论:
- 最大比值的红黑树是通过在每个黑色结点下尽可能多地添加红色子结点来构造的。
- 最小比值的红黑树是通过构造一棵完全平衡的二叉树,其中每个结点都是黑色的。
在实际应用中,红黑树的构造和操作需要考虑更多的细节,包括插入和删除操作后的平衡调整。本文仅提供了构造红黑树的基本思路和代码示例,实际应用中还需要结合红黑树的其他性质和操作来维护树的平衡。