谷歌（Google）历年编程真题——数组和字符串（螺旋矩阵）

news2025/1/17 1:48:45

Google 希望了解你的编码技能和专业技术知识，包括工具、编程语言，以及关于数据结构和算法等主题的一般知识。讨论过程中通常会反复提到相关的话题，就像在工作中的讨论那样，从而推动彼此思考并学习不同的方法。无论你的工作经验如何，Google 都非常重视你的分析能力。请准备好展示你在数据结构和算法方面的扎实功底。

螺旋矩阵

给你一个 m 行 n 列的矩阵 matrix ，请按照顺时针螺旋顺序，返回矩阵中的所有元素。

示例 1：

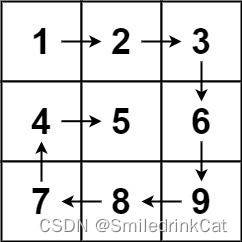
在这里插入图片描述

输入：matrix = [[1,2,3],[4,5,6],[7,8,9]]
输出：[1,2,3,6,9,8,7,4,5]

示例 2：

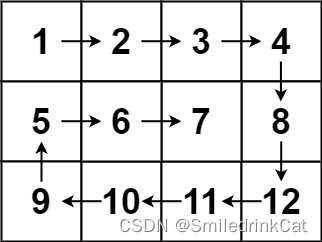
在这里插入图片描述

输入：matrix = [[1,2,3,4],[5,6,7,8],[9,10,11,12]]
输出：[1,2,3,4,8,12,11,10,9,5,6,7]

提示：

m == matrix.length
n == matrix[i].length
1 <= m, n <= 10
-100 <= matrix[i][j] <= 100

思路一：

我们可以按照顺时针螺旋的顺序遍历矩阵，每次取出最外层的元素，并不断缩小矩阵的范围，直到遍历完所有元素。具体步骤如下：

初始化四个变量：上边界 top、下边界 bottom、左边界 left、右边界 right，分别表示当前遍历范围的边界。
按照顺时针螺旋的顺序遍历矩阵，并将元素添加到结果列表中。
每次遍历完一行或一列后，更新边界值，缩小遍历范围。
循环直到所有元素都被遍历完。

代码示例1：

def spiralOrder(matrix):
    if not matrix:
        return []

    result = []
    m, n = len(matrix), len(matrix[0])
    top, bottom, left, right = 0, m - 1, 0, n - 1

    while top <= bottom and left <= right:
        # 从左到右遍历上边界
        for i in range(left, right + 1):
            result.append(matrix[top][i])
        top += 1

        # 从上到下遍历右边界
        for i in range(top, bottom + 1):
            result.append(matrix[i][right])
        right -= 1

        # 从右到左遍历下边界
        if top <= bottom:
            for i in range(right, left - 1, -1):
                result.append(matrix[bottom][i])
            bottom -= 1

        # 从下到上遍历左边界
        if left <= right:
            for i in range(bottom, top - 1, -1):
                result.append(matrix[i][left])
            left += 1

    return result

# 示例 1
matrix1 = [[1,2,3],[4,5,6],[7,8,9]]
print(spiralOrder(matrix1)) # 输出：[1,2,3,6,9,8,7,4,5]

# 示例 2
matrix2 = [[1,2,3,4],[5,6,7,8],[9,10,11,12]]
print(spiralOrder(matrix2)) # 输出：[1,2,3,4,8,12,11,10,9,5,6,7]

这个函数首先初始化四个变量表示当前遍历范围的边界。然后按照顺时针螺旋的顺序遍历矩阵，并将元素添加到结果列表中。每次遍历完一行或一列后，更新边界值，缩小遍历范围。最后返回结果列表。

思路二：

另一种解题思路是模拟整个顺时针螺旋的过程，按照方向逐步移动并填入元素。具体步骤如下：

初始化结果数组 result 和方向数组 directions。
依次填入元素，按照右、下、左、上的方向移动，直到遍历完所有元素。
在每个方向上移动的过程中，需要注意边界条件，以及当遍历完某一行或某一列后需要更新边界。
循环直到遍历完所有元素。

代码示例2：

def spiralOrder(matrix):
    if not matrix:
        return []

    result = []
    directions = [(0, 1), (1, 0), (0, -1), (-1, 0)]  # 右、下、左、上
    m, n = len(matrix), len(matrix[0])
    visited = [[False] * n for _ in range(m)]  # 标记已经访问过的元素
    row, col = 0, 0
    direction_index = 0

    for _ in range(m * n):
        result.append(matrix[row][col])
        visited[row][col] = True

        next_row, next_col = row + directions[direction_index][0], col + directions[direction_index][1]
        if 0 <= next_row < m and 0 <= next_col < n and not visited[next_row][next_col]:
            row, col = next_row, next_col
        else:
            direction_index = (direction_index + 1) % 4
            row, col = row + directions[direction_index][0], col + directions[direction_index][1]

    return result

# 示例 1
matrix1 = [[1,2,3],[4,5,6],[7,8,9]]
print(spiralOrder(matrix1)) # 输出：[1,2,3,6,9,8,7,4,5]

# 示例 2
matrix2 = [[1,2,3,4],[5,6,7,8],[9,10,11,12]]
print(spiralOrder(matrix2)) # 输出：[1,2,3,4,8,12,11,10,9,5,6,7]