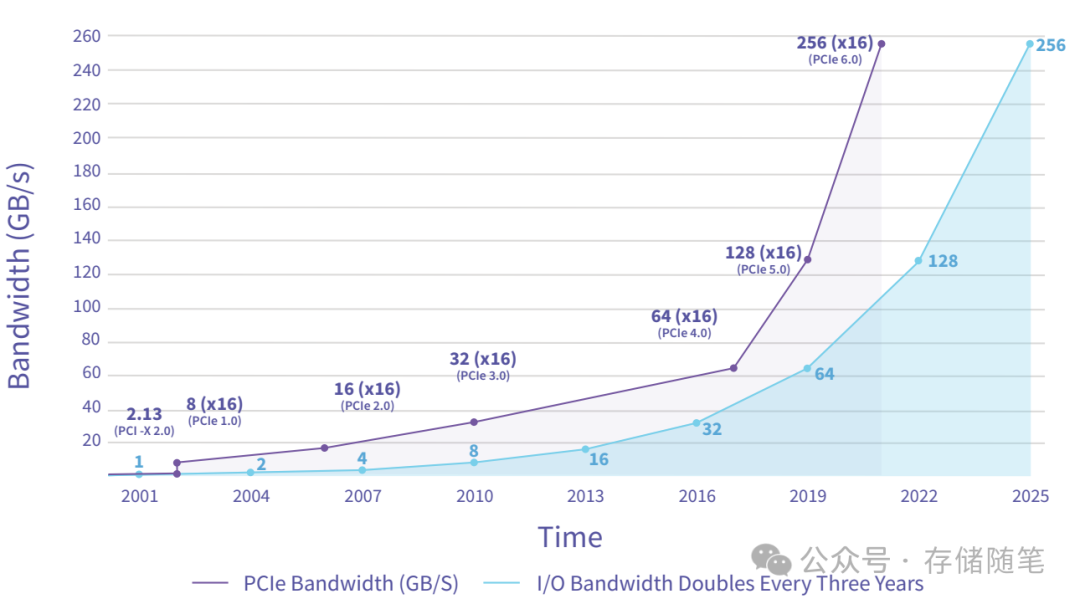
PCIe 6.0都已经发布了2-3年了，目前业内生态还没完全建立。甚至很多人都还没用上PCIe 5.0呢！

近日，PCIe 7.0 ver0.5版本已经开放，同时宣布马不停蹄准备在2025年完成正式SPEC规范发布。

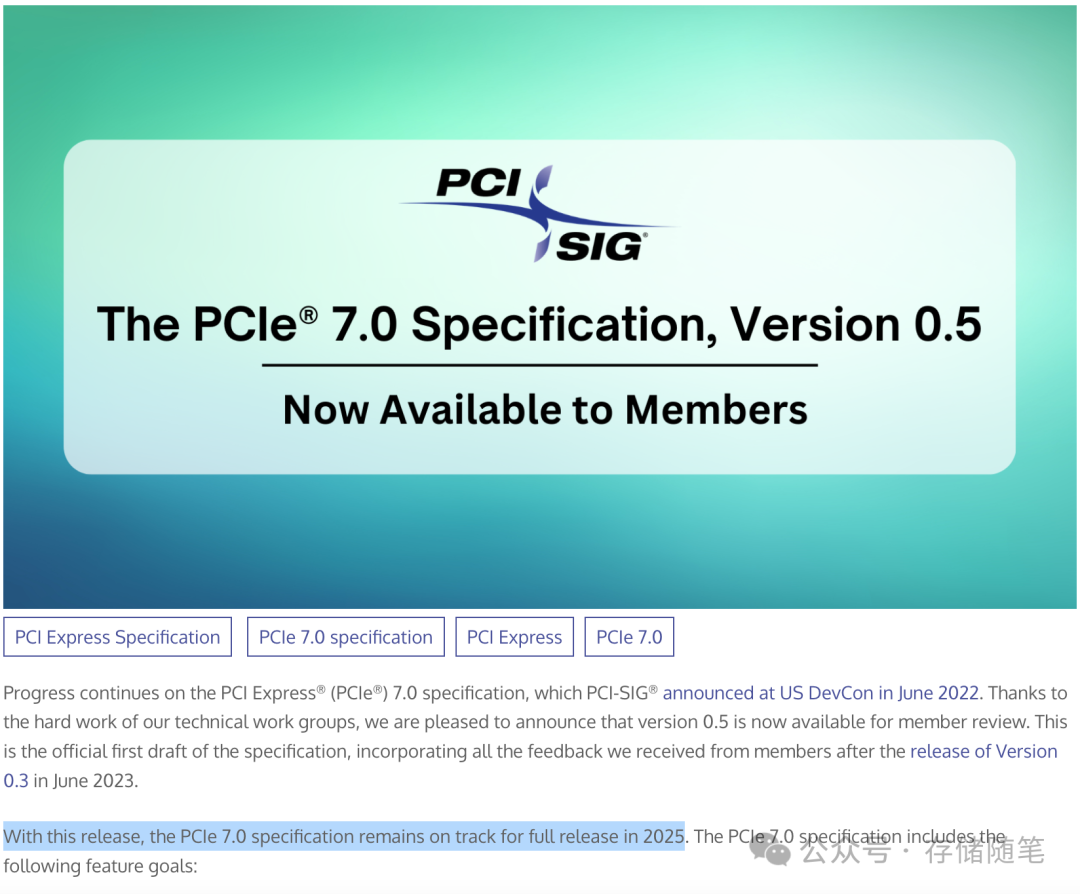
回顾PCIe 7.0变更，PCI-SIG在2022年6月的美国开发者大会（US DevCon）上宣布了PCI Express 7.0规范的持续进展。2023年6月发布版本0.3。PCIe 7.0规范旨在实现以下特性目标：

1. 提供高达128 GT/s的原始比特率：通过x16配置实现双向最高可达512 GB/s的数据传输速率，显著提升带宽能力以应对大数据量应用的需求。

2. 采用PAM4（四电平脉冲幅度调制）信号：采用更先进的调制技术，通过在信号上编码四个不同的振幅级别，提高单位时间内传输的信息密度。

3. 聚焦信道参数与传输距离：优化信道设计参数，确保在更长的物理距离下仍能保持高数据传输速率和稳定性，这对于数据中心等大规模部署环境至关重要。

4. 保持低延迟与高可靠性：继续追求低延迟性能，并强化系统的鲁棒性和数据传输的准确性，以适应对实时性和数据完整性要求极高的应用场景。

5. 提升电源效率：在提高性能的同时注重节能，致力于降低每比特数据传输的能耗，符合现代数据中心对绿色计算和能源效益的追求。

6. 保持与前代PCIe技术的向后兼容：确保新规范与所有先前PCIe版本的硬件设备无缝对接，保护用户投资并简化升级路径。

PCIe协议跑得太快，让开发同学们都受不了（借鉴下在执行pcie 6.0相关文章中，粉丝朋友留言交流的内容），强烈建议PCIe 7.0先躺平一段时间～劝你不要太卷啦～让开发同学们也缓口气～

扩展阅读：

• PCIe 6.0生态业内进展分析总结

• 浅析PCIe 6.0功能更新与实现的挑战

• 国产"芯"希望｜PCIe 5.0 SSD以后就靠它了～

• PCIe P2P DMA全景解读

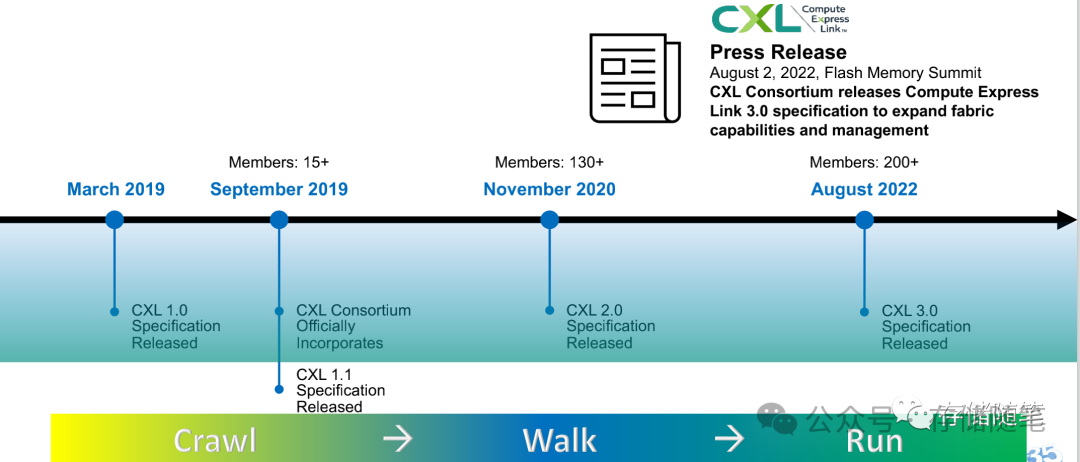
与PCIe协议强绑定的CXL，想必目前也是压力山大了。基于PCIe 5.0的CXL 1.1/2.0生态都没形成，基于PCIe 6.0的CXL 3.0仍然还有一段很长路要走。PCIe 7.0明年送到面前了，你让CXL咋办？

CXL 1.1（PCIe 5.0）支持直接内存扩展器连接。CXL 2.0（PCIe 5.0）将引入CXL交换机，扩展内存池功能。同时，CXL 3.0利用PCIe 6.0将启用级联交换机和点对点连接，促进完整的服务器解聚和可组合性。CXL标准包括三种协议（CXL.io、CXL.cache和CXL.mem），支持三种不同的CXL设备类型。这三种CXL设备类型，目前来看，Type3内存扩展方案的发展最迅速，也是带给数据中心和内存厂商最大的机遇。

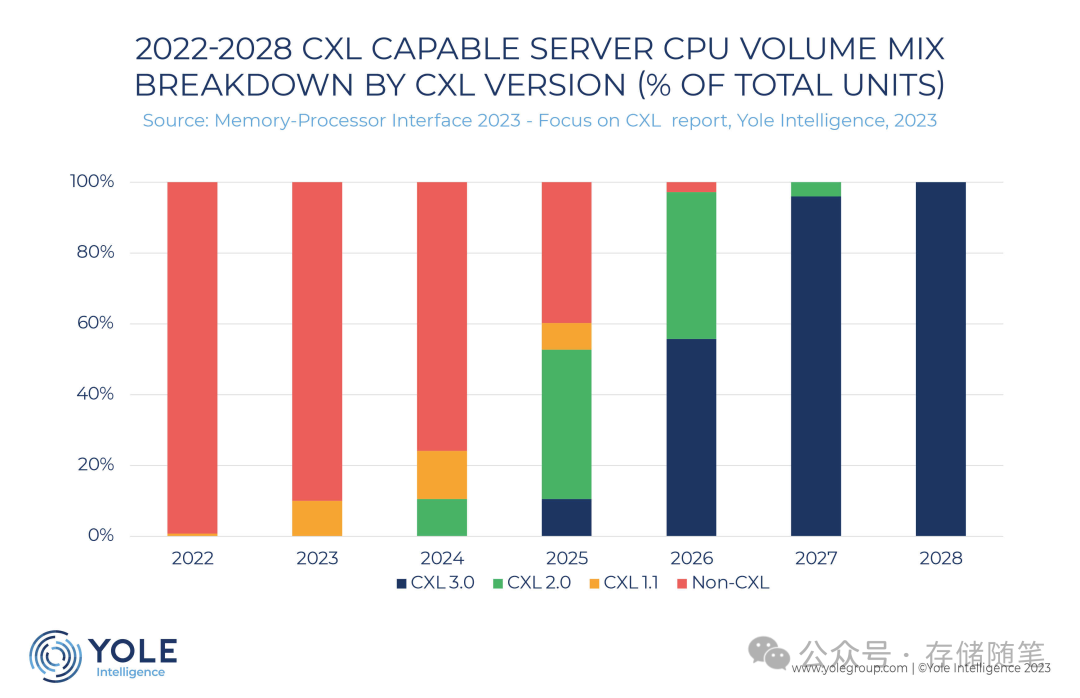
根据Yole机构分析数据显示，CXL在2024年开始爬坡，在2025年将会大规模上量，也就是代表着CXL的时代从2025年开始正式到来。

扩展阅读：

• CXL崛起：2024启航，2025年开启新时代

• 是谁？阻止CXL在AI场景大展身手～

• 浅析CXL P2P DMA加速数据传输的原理

如果您看完有所受益，欢迎点击文章底部左下角“关注”并点击“分享”、“在看”，非常感谢！

精彩推荐:

• 3D DRAM虽困难重重，最快明年到来

• 字节跳动入局存储内存SCM

• 解读“CFMS中国闪存市场峰会”存储技术看点

• 首个业内DNA存储技术规范发布

• 如何突破SSD容量提升的瓶颈？

• 固态存储是未来｜浅析SSD架构的演进与创新技术

• 论文解读：NAND闪存中读电压和LDPC纠错码的高效设计

• 华为新发布磁电存储“王炸”，到底是什么？

• SSD LDPC软错误探测方案解读

• 关于SSD LDPC纠错能力的基础探究

• 存储系统如何规避数据静默错误？

• PCIe P2P DMA全景解读

• 深度解读NVMe计算存储协议

• 对于超低延迟SSD，IO调度器已经过时了吗？

• 浅析CXL P2P DMA加速数据传输的原理

• NVMe over CXL技术如何加速Host与SSD数据传输？

• 浅析LDPC软解码对SSD延迟的影响

• 为什么QLC NAND才是ZNS SSD最大的赢家？

• SSD在AI发展中的关键作用：从高速缓存到数据湖

• 浅析不同NAND架构的差异与影响

• SSD基础架构与NAND IO并发问题探讨

• 字节跳动ZNS SSD应用案例解析

• CXL崛起：2024启航，2025年开启新时代

• NVMe SSD：ZNS与FDP对决，你选谁？

• 浅析PCI配置空间

• 浅析PCIe系统性能

• 存储随笔《NVMe专题》大合集及PDF版正式发布！

如果您也想针对存储行业分享自己的想法和经验，诚挚欢迎您的大作。
投稿邮箱：Memory_logger@163.com （投稿就有惊喜哦~）

《存储随笔》自媒体矩阵

更多存储随笔科普视频讲解，请移步B站账号：

如您有任何的建议与指正，敬请在文章底部留言，感谢您不吝指教！如有相关合作意向，请后台私信，小编会尽快给您取得联系，谢谢！