1. introduction_to_pca.cpp 主成分分析


/**
* @file introduction_to_pca.cpp
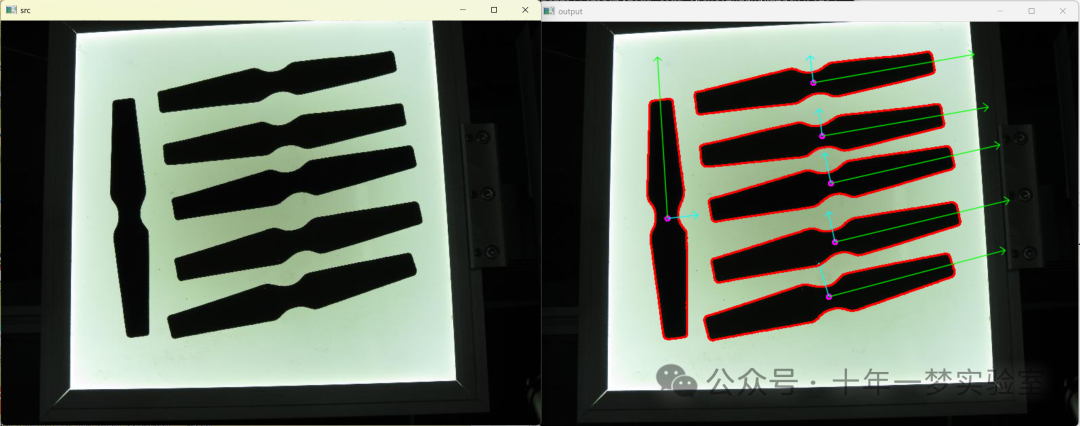
* @brief 这个程序演示了如何使用OpenCV PCA 提取物体的方向
* @author OpenCV团队
*/
// 包含OpenCV函数库所需要的头文件
#include "opencv2/core.hpp"
#include "opencv2/imgproc.hpp"
#include "opencv2/highgui.hpp"
#include <iostream> // 包含输入输出流的头文件
// 使用std和cv的命名空间,这样我们就可以直接使用它们提供的方法,不用每次都写std::和cv::
using namespace std;
using namespace cv;
// 函数声明
void drawAxis(Mat&, Point, Point, Scalar, const float);
double getOrientation(const vector<Point> &, Mat&);
/**
* @function drawAxis
* @brief 绘制轴线的函数
*/
void drawAxis(Mat& img, Point p, Point q, Scalar colour, const float scale = 0.2)
{
//! [visualization1]
// 计算以弧度为单位的角度
double angle = atan2((double)p.y - q.y, (double)p.x - q.x); // p到q的线段角度
// 计算p和q之间的直线的长度
double hypotenuse = sqrt((double)(p.y - q.y) * (p.y - q.y) + (p.x - q.x) * (p.x - q.x));
// 这里通过缩放因子来延长线段的长度
q.x = (int)(p.x - scale * hypotenuse * cos(angle)); // 计算新的q点的x坐标
q.y = (int)(p.y - scale * hypotenuse * sin(angle)); // 计算新的q点的y坐标
// 绘制p点到新q点的直线,这是主线段
line(img, p, q, colour, 1, LINE_AA);
// 创建箭头的勾
// 根据箭头角度计算箭头勾的端点,并绘制箭头勾的第一部分
p.x = (int)(q.x + 9 * cos(angle + CV_PI / 4)); // 计算箭头勾的一个端点的x坐标
p.y = (int)(q.y + 9 * sin(angle + CV_PI / 4)); // 计算箭头勾的一个端点的y坐标
line(img, p, q, colour, 1, LINE_AA); // 绘制箭头勾的第一部分
// 绘制箭头勾的第二部分
p.x = (int)(q.x + 9 * cos(angle - CV_PI / 4)); // 计算箭头勾的另一个端点的x坐标
p.y = (int)(q.y + 9 * sin(angle - CV_PI / 4)); // 计算箭头勾的另一个端点的y坐标
line(img, p, q, colour, 1, LINE_AA); // 绘制箭头勾的第二部分
//! [visualization1]
}
/**
* @function getOrientation
* @brief 获取方向的函数
*/
double getOrientation(const vector<Point> &pts, Mat &img)
{
//! [pca]
// 构造PCA分析使用的数据缓冲区, 每个点的x和y坐标为一行
int sz = static_cast<int>(pts.size()); // 获取点集的大小
Mat data_pts = Mat(sz, 2, CV_64F); // 创建Mat对象用于存储点坐标
for (int i = 0; i < data_pts.rows; i++) // 遍历所有点
{
data_pts.at<double>(i, 0) = pts[i].x; // 将点的x坐标放入Mat对象
data_pts.at<double>(i, 1) = pts[i].y; // 将点的y坐标放入Mat对象
}
// 执行PCA分析
PCA pca_analysis(data_pts, Mat(), PCA::DATA_AS_ROW); // 使用点集进行PCA分析
// 获取物体的中心点
Point cntr = Point(static_cast<int>(pca_analysis.mean.at<double>(0, 0)), // 计算平均值点的x坐标
static_cast<int>(pca_analysis.mean.at<double>(0, 1))); // 计算平均值点的y坐标
// 储存特征值和特征向量
vector<Point2d> eigen_vecs(2); // 创建存储特征向量的向量
vector<double> eigen_val(2); // 创建存储特征值的向量
for (int i = 0; i < 2; i++) // 只考虑x和y坐标,因此遍历两个维度
{
eigen_vecs[i] = Point2d(pca_analysis.eigenvectors.at<double>(i, 0), // 获取第i个特征向量的x分量
pca_analysis.eigenvectors.at<double>(i, 1)); // 获取第i个特征向量的y分量
eigen_val[i] = pca_analysis.eigenvalues.at<double>(i); // 获取第i个特征值
}
//! [pca]
//! [visualization]
// 画出主成分,也即特征向量方向
circle(img, cntr, 3, Scalar(255, 0, 255), 2); // 在中心点画个小圆标记
// 根据特征值和特征向量计算两个特征点的位置
Point p1 = cntr + 0.02 * Point(static_cast<int>(eigen_vecs[0].x * eigen_val[0]), static_cast<int>(eigen_vecs[0].y * eigen_val[0]));
Point p2 = cntr - 0.02 * Point(static_cast<int>(eigen_vecs[1].x * eigen_val[1]), static_cast<int>(eigen_vecs[1].y * eigen_val[1]));
// 画出两个特征向量构成的轴
drawAxis(img, cntr, p1, Scalar(0, 255, 0), 1); // 第一个主成分用绿色表示
drawAxis(img, cntr, p2, Scalar(255, 255, 0), 5); // 第二个主成分用黄色表示
// 计算并返回第一个主成分的方向角度(弧度值)
double angle = atan2(eigen_vecs[0].y, eigen_vecs[0].x); // orientation in radians
//! [visualization]
return angle; // 返回物体的定向角度
}
/**
* @function main
* @brief 主函数
*/
int main(int argc, char** argv)
{
//! [pre-process]
// 加载图像
CommandLineParser parser(argc, argv, "{@input | pca_test1.jpg | input image}");
parser.about( "This program demonstrates how to use OpenCV PCA to extract the orientation of an object.\n" );
parser.printMessage();
// 从文件中读取图像
Mat src = imread( samples::findFile( parser.get<String>("@input") ) );
// 检查图像是否成功加载
if(src.empty())
{
cout << "Problem loading image!!!" << endl;
return EXIT_FAILURE;
}
// 显示原始图像
imshow("src", src);
// 将图像转换为灰度图
Mat gray;
cvtColor(src, gray, COLOR_BGR2GRAY);
// 将图像转换为二值图
Mat bw;
threshold(gray, bw, 50, 255, THRESH_BINARY | THRESH_OTSU);
//! [pre-process]
//! [contours]
// 在阈值处理后的图像中查找所有轮廓
vector<vector<Point> > contours;
findContours(bw, contours, RETR_LIST, CHAIN_APPROX_NONE);
for (size_t i = 0; i < contours.size(); i++)
{
// 计算每个轮廓的面积
double area = contourArea(contours[i]);
// 忽略面积太小或太大的轮廓
if (area < 1e2 || 1e5 < area) continue;
// 仅用于可视化目的绘制每个轮廓
drawContours(src, contours, static_cast<int>(i), Scalar(0, 0, 255), 2);
// 获取每个形状的方向
getOrientation(contours[i], src);
}
//! [contours]
// 显示处理结果图像
imshow("output", src);
// 等待用户操作
waitKey();
// 正常退出程序
return EXIT_SUCCESS;
}该段代码主要演示了如何使用OpenCV里的PCA方法来提取物体的方向。它包括以下几个部分:
获取轮廓并绘制。
使用PCA计算轮廓的方向。
在图像上以直观的方式绘制轴线和方向。
主要的应用场景是,当你有一些形状,并且你想要定量地分析它们的方向时,可以使用这段代码来帮助你提取每个形状的主要方向。
threshold(gray, bw, 50, 255, THRESH_BINARY | THRESH_OTSU);

findContours(bw, contours, RETR_LIST, CHAIN_APPROX_NONE);

2. introduction_to_svm.cpp
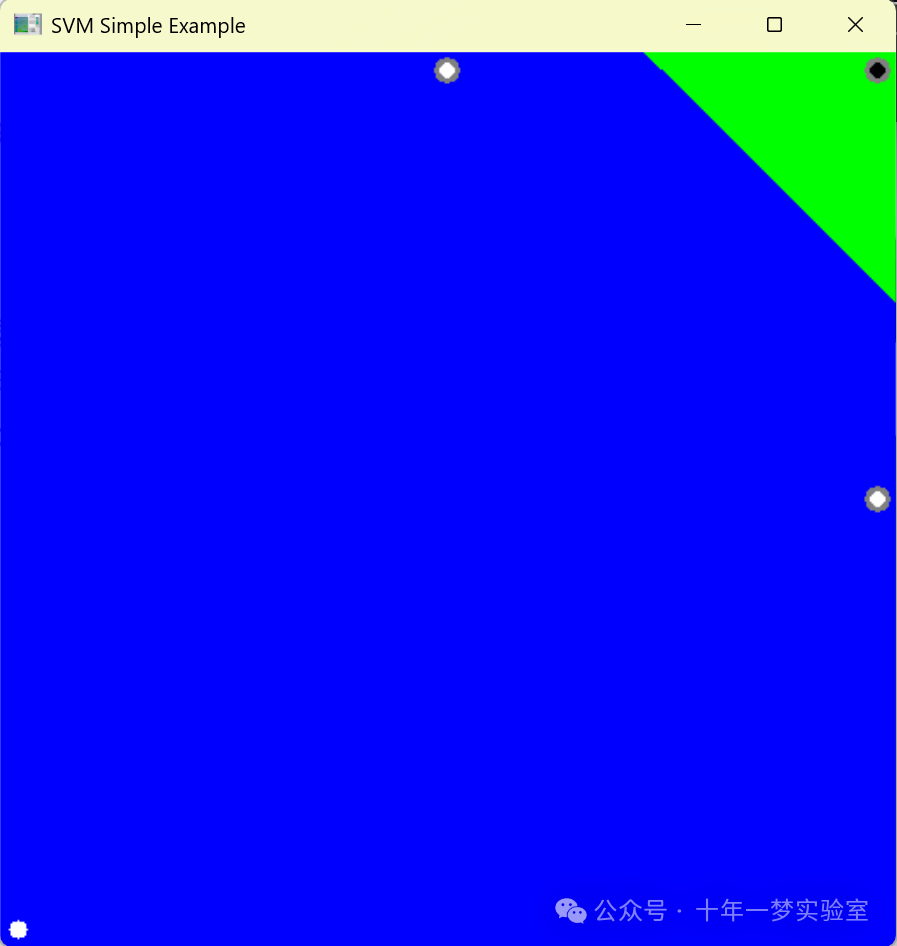

该代码的主要功能是使用支持向量机 (SVM) 对简单的2D数据进行分类,并把结果可视化展示出来。它首先设定了一个简单的二维训练数据集和对应的标签,然后创建了一个SVM分类器,并用线性核函数来训练这些数据。之后创建了一个512x512大小的图像,该图像的每个像素代表一个数据点,通过SVM模型对每个点进行分类,并据此为点涂色(绿色为正类,蓝色为负类)。代码还显示了训练数据点,并用不同的颜色标注支持向量。最终,结果图像会被保存并显示给用户。
# 包含OpenCV库相关头文件
#include <opencv2/core.hpp> // 包含OpenCV内核模块的定义
#include <opencv2/imgproc.hpp> // 包含图像处理功能
#include <opencv2/imgcodecs.hpp> // 包含图像编码解码相关功能
#include <opencv2/highgui.hpp> // 包含图形用户界面相关功能
#include <opencv2/ml.hpp> // 包含机器学习模块的功能
// 使用命名空间,简化代码
using namespace cv;
using namespace cv::ml;
int main(int, char**)
{
// 设置训练数据
// [setup1]
int labels[4] = {1, -1, -1, -1}; // 定义标签数组,一类用1表示,另一类用-1表示
float trainingData[4][2] = { {501, 10}, {255, 10}, {501, 255}, {10, 501} }; // 定义训练数据数组
// [setup1]
// [setup2]
Mat trainingDataMat(4, 2, CV_32F, trainingData); // 将训练数据转换为OpenCV矩阵
Mat labelsMat(4, 1, CV_32SC1, labels); // 将标签数据转换为OpenCV矩阵
// [setup2]
// 训练SVM分类器
// [init]
Ptr<SVM> svm = SVM::create(); // 创建一个SVM对象
svm->setType(SVM::C_SVC); // 设置SVM类型为C-Support Vector Classification
svm->setKernel(SVM::LINEAR); // 设置SVM核函数为线性核
svm->setTermCriteria(TermCriteria(TermCriteria::MAX_ITER, 100, 1e-6)); // 设置终止条件
// [init]
// [train]
svm->train(trainingDataMat, ROW_SAMPLE, labelsMat); // 用训练数据和标签训练SVM
// [train]
// 为了可视化,定义图像尺寸和图像矩阵
int width = 512, height = 512;
Mat image = Mat::zeros(height, width, CV_8UC3);
// 展示SVM给出的决策区域
// [show]
Vec3b green(0,255,0), blue(255,0,0);
for (int i = 0; i < image.rows; i++)
{
for (int j = 0; j < image.cols; j++)
{
Mat sampleMat = (Mat_<float>(1,2) << j,i); // 创建一个样本点
float response = svm->predict(sampleMat); // 预测样本点的响应
if (response == 1)
image.at<Vec3b>(i,j) = green; // 如果预测结果为1,将该点标记为绿色
else if (response == -1)
image.at<Vec3b>(i,j) = blue; // 如果预测结果为-1,将该点标记为蓝色
}
}
// [show]
// 展示训练数据
// [show_data]
int thickness = -1; // 设置圆点的厚度为-1,即实心圆点
// 在图像中绘制训练数据点
circle( image, Point(501, 10), 5, Scalar( 0, 0, 0), thickness );
circle( image, Point(255, 10), 5, Scalar(255, 255, 255), thickness );
circle( image, Point(501, 255), 5, Scalar(255, 255, 255), thickness );
circle( image, Point( 10, 501), 5, Scalar(255, 255, 255), thickness );
// [show_data]
// 展示支持向量
// [show_vectors]
thickness = 2; // 设置支持向量圆点的厚度为2
Mat sv = svm->getUncompressedSupportVectors(); // 获取未压缩的支持向量
// 在图像上绘制支持向量点
for (int i = 0; i < sv.rows; i++)
{
const float* v = sv.ptr<float>(i); // 获取每个支持向量的指针
circle(image, Point( (int) v[0], (int) v[1]), 6, Scalar(128, 128, 128), thickness); // 绘制支持向量点
}
// [show_vectors]
imwrite("result.png", image); // 将图像保存为result.png文件
imshow("SVM Simple Example", image); // 将图像显示给用户
waitKey(); // 等待用户按键
return 0;
}

3. non_linear_svms.cpp

#include <iostream> // 引入IO流库
#include <opencv2/core.hpp> // 引入OpenCV核心功能库
#include <opencv2/imgproc.hpp> // 引入图像处理库
#include "opencv2/imgcodecs.hpp" // 引入图像编解码库
#include <opencv2/highgui.hpp> // 引入GUI库
#include <opencv2/ml.hpp> // 引入机器学习库
using namespace cv; // 使用cv命名空间
using namespace cv::ml; // 使用cv的机器学习命名空间
using namespace std; // 使用标准命名空间
// 声明一个帮助函数,用于显示程序信息
static void help()
{
cout<< "\n--------------------------------------------------------------------------" << endl
<< "This program shows Support Vector Machines for Non-Linearly Separable Data. " << endl
<< "--------------------------------------------------------------------------" << endl
<< endl;
}
// 主函数入口
int main()
{
help(); // 调用帮助函数展示信息
// 定义一些SVM训练时使用的常量
const int NTRAINING_SAMPLES = 100; // 每个类的训练样本数
const float FRAC_LINEAR_SEP = 0.9f; // 线性可分部分的样本比例
// 用于可视化的数据
const int WIDTH = 512, HEIGHT = 512; // 定义可视化图像的宽和高
Mat I = Mat::zeros(HEIGHT, WIDTH, CV_8UC3); // 创建一个黑色的可视化图像
//--------------------- 1. 随机设置训练数据 ---------------------------------------
Mat trainData(2*NTRAINING_SAMPLES, 2, CV_32F); // 创建训练数据矩阵
Mat labels (2*NTRAINING_SAMPLES, 1, CV_32S); // 创建对应的标签矩阵
RNG rng(100); // 随机数生成器
// 设置线性可分部分的训练数据
int nLinearSamples = (int) (FRAC_LINEAR_SEP * NTRAINING_SAMPLES);
// 类别1的随机点生成
Mat trainClass = trainData.rowRange(0, nLinearSamples);
// x坐标的范围是[0, 0.4)
Mat c = trainClass.colRange(0, 1);
rng.fill(c, RNG::UNIFORM, Scalar(0), Scalar(0.4 * WIDTH));
// y坐标的范围是[0, 1)
c = trainClass.colRange(1,2);
rng.fill(c, RNG::UNIFORM, Scalar(0), Scalar(HEIGHT));
// 类别2的随机点生成
trainClass = trainData.rowRange(2*NTRAINING_SAMPLES-nLinearSamples, 2*NTRAINING_SAMPLES);
// x坐标的范围是[0.6, 1]
c = trainClass.colRange(0 , 1);
rng.fill(c, RNG::UNIFORM, Scalar(0.6*WIDTH), Scalar(WIDTH));
// y坐标的范围是[0, 1)
c = trainClass.colRange(1,2);
rng.fill(c, RNG::UNIFORM, Scalar(0), Scalar(HEIGHT));
//------------------ 生成非线性可分部分的训练数据 ---------------
// 为类别1和2的生成随机点
trainClass = trainData.rowRange(nLinearSamples, 2*NTRAINING_SAMPLES-nLinearSamples);
// x坐标的范围是[0.4, 0.6)
c = trainClass.colRange(0,1);
rng.fill(c, RNG::UNIFORM, Scalar(0.4*WIDTH), Scalar(0.6*WIDTH));
// y坐标的范围是[0, 1)
c = trainClass.colRange(1,2);
rng.fill(c, RNG::UNIFORM, Scalar(0), Scalar(HEIGHT));
//------------------------ 生成类别的标签 ---------------------------------
labels.rowRange( 0, NTRAINING_SAMPLES).setTo(1); // 类别1
labels.rowRange(NTRAINING_SAMPLES, 2*NTRAINING_SAMPLES).setTo(2); // 类别2
//------------------------ 2. 设置支持向量机的参数 -------------------------
cout << "Starting training process" << endl;
Ptr<SVM> svm = SVM::create(); // 创建一个SVM对象
svm->setType(SVM::C_SVC); // 设置SVM类型为C-SVC
svm->setC(0.1); // 设置C参数
svm->setKernel(SVM::LINEAR); // 设置核函数为线性核
svm->setTermCriteria(TermCriteria(TermCriteria::MAX_ITER, (int)1e7, 1e-6)); // 设置终止条件
//------------------------ 3. 训练svm --------------------------------------
svm->train(trainData, ROW_SAMPLE, labels); // 使用训练数据和标签训练SVM
cout << "Finished training process" << endl;
//------------------------ 4. 显示决策区域-----------------------------------
Vec3b green(0,100,0), blue(100,0,0);
for (int i = 0; i < I.rows; i++)
{
for (int j = 0; j < I.cols; j++)
{
// 对于图像中的每个点,使用SVM进行预测
Mat sampleMat = (Mat_<float>(1,2) << j, i);
float response = svm->predict(sampleMat);
// 根据预测结果把点对应的颜色涂上
if (response == 1) I.at<Vec3b>(i,j) = green;
else if (response == 2) I.at<Vec3b>(i,j) = blue;
}
}
//----------------------- 5. 显示训练数据 -----------------------------------
int thick = -1;
float px, py;
// 类别1的数据
for (int i = 0; i < NTRAINING_SAMPLES; i++)
{
px = trainData.at<float>(i,0);
py = trainData.at<float>(i,1);
// 在图像上画圆来代表数据点
circle(I, Point( (int) px, (int) py ), 3, Scalar(0, 255, 0), thick);
}
// 类别2的数据
for (int i = NTRAINING_SAMPLES; i <2*NTRAINING_SAMPLES; i++)
{
px = trainData.at<float>(i,0);
py = trainData.at<float>(i,1);
circle(I, Point( (int) px, (int) py ), 3, Scalar(255, 0, 0), thick);
}
//------------------------- 6. 显示支持向量 ---------------------------------
thick = 2;
Mat sv = svm->getUncompressedSupportVectors(); // 获取支持向量
for (int i = 0; i < sv.rows; i++)
{
const float* v = sv.ptr<float>(i);
// 画出支持向量
circle(I, Point( (int) v[0], (int) v[1]), 6, Scalar(128, 128, 128), thick);
}
imwrite("result.png", I); // 保存生成的图像
imshow("SVM for Non-Linear Training Data", I); // 展示图像
waitKey(); // 等待键盘输入
return 0;
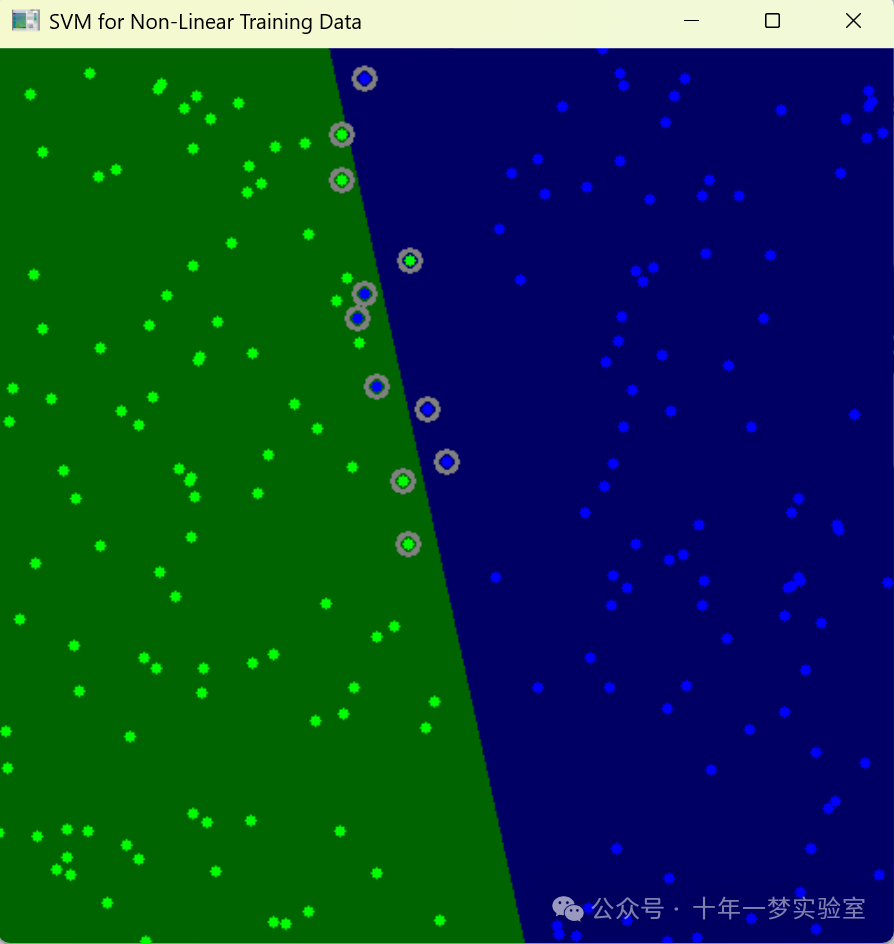
}本段代码演示了如何使用支持向量机(SVM)对非线性可分数据进行分类。具体包括以下步骤:
随机生成两个类的训练数据和对应的标签;
设置支持向量机的参数并进行训练;
显示SVM的决策区域;
在图像上用不同颜色显示两个类的数据点;
在图像上显示支持向量。
代码运行完成后将会产生一张图像,展示了决策区域和支持向量机如何区分两个类的数据点。





circle(I, Point((int)px, (int)py), 3, Scalar(255, 0, 0), thick);