蓝桥杯第十四届C++A组(未完)

【规律题】平方差

题目描述

给定 L, R，问 L ≤ x ≤ R 中有多少个数 x 满足存在整数 y,z 使得 $x=y^{2}-z^{2}$ 。

输入格式

输入一行包含两个整数 L, R，用一个空格分隔。

输出格式

输出一行包含一个整数满足题目给定条件的 x 的数量。

样例输入

1 5

样例输出

提示

$1=1^{2}-0^{2}$

$3=2^{2}-1^{2}$

$4=2^{2}-0^{2}$

$5=3^{2}-2^{2}$

对于 40% 的评测用例，LR ≤ 5000 ；

对于所有评测用例，1 ≤ L ≤ R ≤ 10^9 。

由 $x=y^{2}-z^{2}$ 得 $x=(y+z)*(y-z)$ ，

令 $m=(y+z),n=(y-z)$ ，则 $x=m*n$ ，解得： $y=\frac{m+n}{2},z=\frac{m-n}{2}$

要使y和z有整数解，那么 $(m+n),(m-n)$ 为偶数，

（1）偶数+偶数=偶数，偶数-偶数=偶数；

（2）奇数+奇数=偶数，奇数-奇数=偶数；

则m和n奇偶性相同，即如果x有一对因子奇偶性相同，那么一定可以找到y,z满足 $x=y^{2}-z^{2}$ 。

（1）若m,n都为偶数，那么m是2的倍数，n是2的倍数，那么m*n一定是4的倍数。

（2）若m,n都为奇数，那么由性质奇数*奇数=奇数得，m*n也一定为奇数。

综上 x 是四的倍数或者奇数。

#include<iostream>
#include<cstring>
#include<map>
#include<vector>
#include<cmath>
using namespace std;
typedef long long LL;
const int N=10010;
int main(){
	LL L,R;
	cin>>L>>R;
	int cnt=0;
	for(LL i=L;i<=R;i++){
		if(i%4==0||i%2){
			cnt++;
		}
	}
	cout<<cnt<<endl;
	return 0;
}

更小的数

题目描述

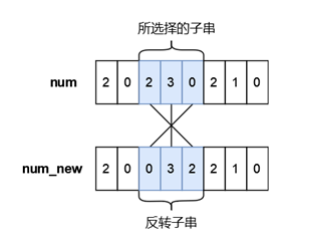
蓝桥杯2023年第十四届省赛真题-更小的数

小蓝有一个长度均为 n 且仅由数字字符 0 ∼ 9 组成的字符串，下标从 0 到 n − 1，你可以将其视作是一个具有 n 位的十进制数字 num，小蓝可以从 num 中选出一段连续的子串并将子串进行反转，最多反转一次。小蓝想要将选出的子串进行反转后再放入原位置处得到的新的数字 numnew 满足条件 numnew < num，请你帮他计算下一共有多少种不同的子串选择方案，只要两个子串在 num 中的位置不完全相同我们就视作是不同的方案。

注意，我们允许前导零的存在，即数字的最高位可以是 0 ，这是合法的。

输入格式

输入一行包含一个长度为 n 的字符串表示 num（仅包含数字字符 0 ∼ 9），

从左至右下标依次为 0 ∼ n − 1。

输出格式

输出一行包含一个整数表示答案。

样例输入

样例输出

提示

一共有 8 种不同的方案：

1）所选择的子串下标为 0 ∼ 1 ，反转后的 numnew = 120102 < 210102 ；

2）所选择的子串下标为 0 ∼ 2 ，反转后的 numnew = 012102 < 210102 ；

3）所选择的子串下标为 0 ∼ 3 ，反转后的 numnew = 101202 < 210102 ；

4）所选择的子串下标为 0 ∼ 4 ，反转后的 numnew = 010122 < 210102 ；

5）所选择的子串下标为 0 ∼ 5 ，反转后的 numnew = 201012 < 210102 ；

6）所选择的子串下标为 1 ∼ 2 ，反转后的 numnew = 201102 < 210102 ；

7）所选择的子串下标为 1 ∼ 4 ，反转后的 numnew = 201012 < 210102 ；

8）所选择的子串下标为 3 ∼ 4 ，反转后的 numnew = 210012 < 210102 ；

对于 20% 的评测用例，1 ≤ n ≤ 100 ；

对于 40% 的评测用例，1 ≤ n ≤ 1000 ；

对于所有评测用例，1 ≤ n ≤ 5000 。

#include<iostream>
#include<algorithm>
#include<cstring>
#include<map>
#include<vector>
#include<cmath>
using namespace std;
typedef long long LL;
int main(){
	string s;
	cin>>s;
	int n=s.size();
	int cnt=0;
	for(int i=0;i<n-1;i++){
		for(int j=n-1;j>i;j--){
			if(s[i]>s[j]) cnt++;
			else if(s[i]==s[j]){
				for(int x=i,y=j;x<y;x++,y--){
					if(s[x]>s[y]){
						cnt++;
						break;
					}else if(s[x]<s[y]) break;
				}
			}
		}
	}
	cout<<cnt<<endl;
	return 0;
}

【DFS】颜色平衡树

题目描述

给定一棵树，结点由 1 至 n 编号，其中结点 1 是树根。树的每个点有一个颜色 Ci。

如果一棵树中存在的每种颜色的结点个数都相同，则我们称它是一棵颜色平衡树。

求出这棵树中有多少个子树是颜色平衡树。

输入格式

输入的第一行包含一个整数 n ，表示树的结点数。

接下来 n 行，每行包含两个整数 Ci , Fi，用一个空格分隔，表示第 i 个结点的颜色和父亲结点编号。

特别地，输入数据保证 F1 为 0 ，也即 1 号点没有父亲结点。保证输入数据是一棵树。

输出格式

输出一行包含一个整数表示答案。

样例输入

样例输出

提示

编号为 1, 3, 5, 6 的 4 个结点对应的子树为颜色平衡树。

对于 30% 的评测用例，n ≤ 200，Ci ≤ 200 ；

对于 60% 的评测用例，n ≤ 5000，Ci ≤ 5000 ；

对于所有评测用例，1 ≤ n ≤ 200000，1 ≤ Ci ≤ 200000，0 ≤ Fi < i 。

#include<iostream>
#include<cstring>
#include<vector>
#include<map>
using namespace std;
const int N=2e5+10;
int c[N];
int ans=0;
int n;
vector<int> g[N];
void add(map<int,int> &cnt,map<int,int> &cnt_nb){
	for(auto mp:cnt_nb){
		int x=mp.first;
		int y=mp.second;
		cnt[x]+=y;
	}
}
map<int,int> dfs(vector<int> *g,int *c,int i){
	int sz=g[i].size();
	map<int,int> cnt;
	if(sz==0){
		cnt[c[i]]=1;
		ans++;
		return cnt;
	}
	cnt[c[i]]=1;
	for(int j=0;j<sz;j++){
		int nb=g[i][j];
		map<int,int> cnt_nb=dfs(g,c,nb);
		add(cnt,cnt_nb);
	}
	int num=cnt[c[i]];
	for(auto mp:cnt){
		int count=mp.second;
		if(count!=num) return cnt;
	}
	ans++;
	return cnt;
}
int main(){
	cin>>n;
	for(int i=0;i<n;i++){
		int f;
		cin>>c[i]>>f;
		if(f>=1) g[f-1].push_back(i);
	}
	dfs(g,c,0);
	cout<<ans<<endl;
	return 0;
}

【DFS】(选不选)买瓜

题目描述

小蓝正在一个瓜摊上买瓜。瓜摊上共有 n 个瓜，每个瓜的重量为 Ai 。

小蓝刀功了得，他可以把任何瓜劈成完全等重的两份，不过每个瓜只能劈一刀。

小蓝希望买到的瓜的重量的和恰好为 m 。

请问小蓝至少要劈多少个瓜才能买到重量恰好为 m 的瓜。如果无论怎样小蓝都无法得到总重恰好为 m 的瓜，请输出 −1 。

输入格式

输入的第一行包含两个整数 n, m，用一个空格分隔，分别表示瓜的个数和小蓝想买到的瓜的总重量。

第二行包含 n 个整数 Ai，相邻整数之间使用一个空格分隔，分别表示每个瓜的重量。

输出格式

输出一行包含一个整数表示答案。

样例输入

3 10
1 3 13

样例输出

提示

对于 20% 的评测用例，∑n≤10；

对于 60% 的评测用例，∑n≤20；

对于所有评测用例，1 ≤n≤30，1≤ Ai ≤ 10^9 ，1 ≤ m ≤ 10^9

#include<iostream>
#include<algorithm>
using namespace std;
typedef long long LL;
const int N=35,INF=0x3f3f3f3f;
LL p[N];
LL a[N];
int n;
LL m;
int ans=INF;
void dfs(int u,LL sum,int cnt){
	if(sum==m){
		ans=min(ans,cnt);
		return ;
	}
	if(cnt>=ans||u>n||sum+p[u]<m||sum>m) return ;
	dfs(u+1,sum+a[u],cnt);
	dfs(u+1,sum+a[u]/2,cnt+1);
	dfs(u+1,sum,cnt);
}
int main(){
	cin>>n>>m;
	m*=2;
	for(int i=1;i<=n;i++){
		cin>>a[i];
		a[i]*=2;
	}
	sort(a+1,a+1+n,greater<int>());
	for(int i=n;i>=1;i--) p[i]=p[i+1]+a[i];
	dfs(1,0,0);
	if(ans==INF) cout<<"-1"<<endl;
	else cout<<ans<<endl;
	return 0;
}

网络稳定性（X)

异或和之和

题目描述

给定一个数组 Ai，分别求其每个子段的异或和，并求出它们的和。或者说，对于每组满足 1 ≤ L ≤ R ≤ n 的 L, R ，求出数组中第 L 至第 R 个元素的异或和。然后输出每组 L, R 得到的结果加起来的值。

输入格式

输入的第一行包含一个整数 n 。

第二行包含 n 个整数 Ai ，相邻整数之间使用一个空格分隔。

输出格式

输出一行包含一个整数表示答案。

样例输入

5
1 2 3 4 5

样例输出

提示

对于 30% 的评测用例，n ≤ 300 ；
对于 60% 的评测用例，n ≤ 5000 ；
对于所有评测用例，1 ≤ n ≤ 105，0 ≤ Ai ≤ 2^20 。

区间[l,r]的异或和可以表示为 $S_{r}\bigoplus S_{l-1}$ ，这样原问题就变成了：求n+1个数两两异或之和，如果 $S_{i}$ 的二进制第 j 位为1（0），我们只需知道 [0,i-1] 这个区间内的数二进制第 j 位为0（1）的个数x，这样s[i]的第 j 位的贡献值为x*2^j；

#include<iostream>
#include<vector>
#include<map>
#define int long long
using namespace std;
const int N=1e5+10;
int a[N][30];
signed main(){
	int n;
	cin>>n;
	int x;
	for(int i=1;i<=n;i++){
		cin>>x;
		for(int j=0;j<=20;j++){
			a[i][j]=(x>>j)&1;
			a[i][j]^=a[i-1][j];
		}
	}
	int ans=0;
	for(int j=0;j<=20;j++){
		map<int,int> mp;
		mp[0]++;
		for(int i=1;i<=n;i++){
			int x=mp[a[i][j]^1];//与第i个数第j位不同的个数
			ans+=(1<<j)*x;
			mp[a[i][j]]++;
		}
	}
	cout<<ans<<endl;
	return 0;
}

#include<iostream>
#include<vector>
#include<map>
#define int long long
using namespace std;
const int N=1e5+10;
int a[N];
int s[N];
int cnt[N][30];
signed main(){
	int n;
	cin>>n;
	int x;
	for(int i=1;i<=n;i++){
		cin>>a[i];
		s[i]=s[i-1]^a[i];
	}
//求n+1个数第j位0和1的个数
	for(int j=0;j<=20;j++){
		for(int i=0;i<=n;i++){
			if(s[i]>>j&1) cnt[j][1]++;
			else cnt[j][0]++;
		}
	}
	int ans=0;
	for(int i=0;i<=20;i++){
//每个1都可以和每个0异或等于1，总数为cnt[i][0]*cnt[i][1]，每个1的贡献值为2^i
		ans+=cnt[i][0]*cnt[i][1]*(1<<i);
	}
	cout<<ans<<endl;
	return 0;
}