引言

之前觉得这个IDA*算法、迭代加深算法很神秘，感觉很难，其实自己学下来感觉其实不难，相反思路非常的简单，清晰明了，我觉得难是因为我之前从来都不写暴力，就算是图论问题我也只写 $BFS$ ，而不写 $DFS$ ，因为前者虽然长但是好写，后者短也不是很难，其实就是自己写得少，再加上之前参加校赛写 $DFS$ 一直没写对，给自己留下了心理阴影了（其实那题本来时间复杂度太高也过不了），所以就处于未知的恐惧，但现在其实迷雾已经慢慢消散了，开始今天的学习了，加油！

---

一、概念

IDA*： $DFS$ 版的 A* 算法，就是对 迭代加深 的一个优化。有一个估价函数，表示从当前状态到终点至少需要的步骤，如果当前状态加上估价函数都到达不了终点，那么就停止搜索。其实就是跟之前的 $DFS优化$ 一样，就是一个 最优性剪枝 而已，把代码看一遍一下就能理解了。

---

二、例题

1.排书

标签：搜索、IDA*

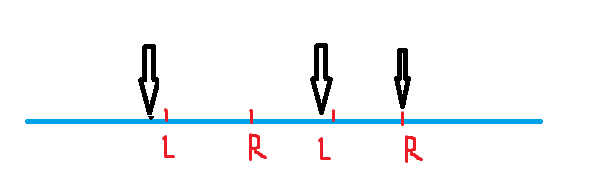
思路：首先答案是在较浅层，所以可以用迭代加深去做。其次估价函数可以这样理解，一次排书会改变 $3$ 个结点的后继，如下图所示，那么最少排书次数为 $\lceil \frac{n}{3}\rceil$ 。剩下的就是正常的迭代加深跟操作了，具体细节见代码。

题目描述：

给定 n 本书，编号为 1∼n。

在初始状态下，书是任意排列的。

在每一次操作中，可以抽取其中连续的一段，再把这段插入到其他某个位置。

我们的目标状态是把书按照 1∼n 的顺序依次排列。

求最少需要多少次操作。

输入格式
第一行包含整数 T，表示共有 T 组测试数据。

每组数据包含两行，第一行为整数 n，表示书的数量。

第二行为 n 个整数，表示 1∼n 的一种任意排列。

同行数之间用空格隔开。

输出格式
每组数据输出一个最少操作次数。

如果最少操作次数大于或等于 5 次，则输出 5 or more。

每个结果占一行。

数据范围
1≤n≤15
输入样例：
3
6
1 3 4 6 2 5
5
5 4 3 2 1
10
6 8 5 3 4 7 2 9 1 10
输出样例：
2
3
5 or more

示例代码：

#include <bits/stdc++.h>

using namespace std;

typedef long long LL;
typedef pair<int,int> PII;
#define x first
#define y second

const int N = 20;

int n;
int q[N];
int w[5][N];

int f()  // 估价函数
{
	int cnt = 0;
	for(int i = 1; i < n; ++i)
	{
		if(q[i] != q[i-1] + 1) cnt++; 
	}
	return (cnt + 2) / 3;
}

bool dfs(int u, int depth)
{
	if(u + f() > depth) return false;  // IDA* 最优性剪枝 
	if(f() == 0) return true;
	
	for(int len = 1; len + 1 <= n; ++len)
	{
		for(int l = 0; l + len - 1 < n; ++l)
		{
			int r = l + len - 1;
			for(int k = r + 1; k < n; ++k) // 排除等效冗余
			{
				memcpy(w[u], q, sizeof q);
				int x, y;
				for(x = r + 1, y = l; x <= k; ++x, ++y) q[y] = w[u][x];
				for(x = l; x <= r; ++x, ++y) q[y] = w[u][x];
				if(dfs(u+1,depth)) return true;
				memcpy(q, w[u], sizeof q);
			}	
		}	
	} 
	return false;
}

int main()
{
	ios::sync_with_stdio(0); cin.tie(0); cout.tie(0);
	
	int T; cin >> T;
	while(T--)
	{
		cin >> n;
		for(int i = 0; i < n; ++i) cin >> q[i];
		
		int depth = 0;
		while(depth < 5 && !dfs(0,depth)) depth++;
		
		if(depth >= 5) cout << "5 or more" << endl;
		else cout << depth << endl;
	}
	
	return 0;
}

---

2.回转游戏

标签：搜索、IDA*

思路：首先步数不会太大，抽 $64$ 次就返回原样了，超过 $64$ 的也是冗余的，所以可以用迭代加深去做。估计函数：没抽一次就会改变一个中间的数，所以至少需要出现次数最多的数全变为一样。然后具体的操作，每个格子可以用如下图进行编号，每次操作就是将每一条格子向前覆盖，然后第一个格子不到后面。又因为从一边抽过再从另一边抽的话就是无效操作，所以可以用一个 $last$ 来记录，然后可以定义一个数组来存其相反的操作。具体细节见代码。

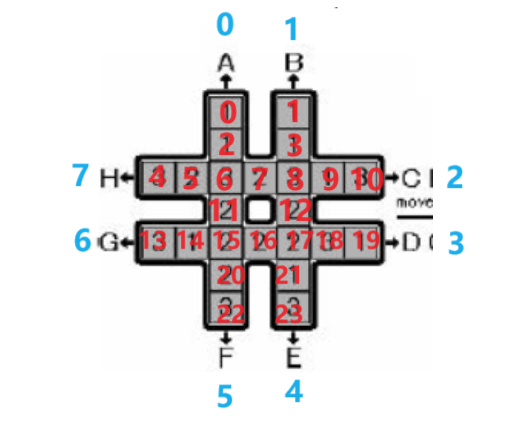
题目描述：

如下图所示，有一个 # 形的棋盘，上面有 1,2,3 三种数字各 8 个。

给定 8 种操作，分别为图中的 A∼H。

这些操作会按照图中字母和箭头所指明的方向，把一条长为 7 的序列循环移动 1 个单位。

例如下图最左边的 # 形棋盘执行操作 A 后，会变为下图中间的 # 形棋盘，再执行操作 C 后会变成下图最右边的 # 形棋盘。

给定一个初始状态，请使用最少的操作次数，使 # 形棋盘最中间的 8 个格子里的数字相同。

输入格式
输入包含多组测试用例。

每个测试用例占一行，包含 24 个数字，表示将初始棋盘中的每一个位置的数字，按整体从上到下，同行从左到右的顺序依次列出。

输入样例中的第一个测试用例，对应上图最左边棋盘的初始状态。

当输入只包含一个 0 的行时，表示输入终止。

输出格式
每个测试用例输出占两行。

第一行包含所有移动步骤，每步移动用大写字母 A∼H 中的一个表示，字母之间没有空格，如果不需要移动则输出 No moves needed。

第二行包含一个整数，表示移动完成后，中间 8 个格子里的数字。

如果有多种方案，则输出字典序最小的解决方案。

输入样例：
1 1 1 1 3 2 3 2 3 1 3 2 2 3 1 2 2 2 3 1 2 1 3 3
1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 3 3 3 3 3 3 3 3
0
输出样例：
AC
2
DDHH
2

示例代码：

#include <bits/stdc++.h>

using namespace std;

typedef long long LL;
typedef pair<int,int> PII;
#define x first
#define y second

const int N = 25;

int q[N];
char path[100];

int op[8][7] = {
	{0,2,6,11,15,20,22},
	{1,3,8,12,17,21,23},
	{10,9,8,7,6,5,4},
	{19,18,17,16,15,14,13},
	{23,21,17,12,8,3,1},
	{22,20,15,11,6,2,0},
	{13,14,15,16,17,18,19},
	{4,5,6,7,8,9,10},
};

int oppsite[8] = {5,4,7,6,1,0,3,2};
int center[8] = {6,7,8,11,12,15,16,17};

int f()
{
	static int sum[4] = {0};
	memset(sum, 0, sizeof sum);
	for(int i = 0; i < 8; ++i) sum[q[center[i]]]++;
	
	int maxv = 0;
	for(int i = 0; i < 4; ++i) maxv = max(maxv, sum[i]);
	return 8 - maxv;
}

void operate(int x)
{
	int t = q[op[x][0]];
	for(int i = 1; i < 7; ++i) q[op[x][i-1]] = q[op[x][i]];
	q[op[x][6]] = t;
}

bool dfs(int u, int depth, int last)
{
	if(u + f() > depth) return false;
	if(f() == 0) return true;
	
	for(int i = 0; i < 8; ++i)
	{
		if(oppsite[i] == last) continue;  // 排除等效冗余
		operate(i);
		path[u] = i + 'A';
		if(dfs(u+1,depth,i)) return true;
		operate(oppsite[i]); 
	}
	return false;
}

int main()
{
	ios::sync_with_stdio(0); cin.tie(0); cout.tie(0);
	
	while(cin >> q[0], q[0])
	{
		for(int i = 1; i < 24; ++i) cin >> q[i];
		
		int depth = 0;
		while(!dfs(0,depth,-1)) depth++;
		
		if(!depth) cout << "No moves needed";
		else
		{
			for(int i = 0; i < depth; ++i) cout << path[i];
		}
		cout << endl << q[6] << endl;
	}
	
	return 0;
}