目录
- 一、说明
- 二、朗之万方程的诞生
- 2.1 牛顿力学
- 2.2 流体中的随机运动
- 三、小质量物体布朗运动方程
- 四、布朗运动的Python代码
- 五、稳定性讨论
- 5.1 波尔兹曼分布
- 5.2 梯度下降算法
- 六、随机梯度下降(SGD)和小批量梯度下降
- 七、机器学习与物理,作为朗之万过程的梯度下降
- 结论
一、说明
梯度下降算法是机器学习中最流行的优化技术之一。它有三种类型:批量梯度下降(GD)、随机梯度下降(SGD)和小批量梯度下降(在每次迭代中用于计算损失函数梯度的数据量不同)。
本文的目标是描述基于朗格文动力学(LD)的全局优化器的研究进展,LD是一种分子运动的建模方法,它起源于20世纪初阿尔伯特·爱因斯坦和保罗·朗之万关于统计力学的著作。
我将从理论物理学的角度提供一个优雅的解释,为什么梯度下降的变种是有效的全局优化器。
二、朗之万方程的诞生

没有迹象表明一场革命即将发生。1904年,如果阿尔伯特·爱因斯坦放弃了物理学,他的科学家同行们可能甚至都不会注意到。幸运的是,这并没有发生。1905年,这位年轻的专利职员发表了四篇革命性的论文。
m
d
2
x
d
t
2
=
−
λ
d
x
d
t
+
R
t
+
F
m \frac{d^2x}{dt^2}=-\lambda\frac{dx}{dt}+R_t + F
mdt2d2x=−λdtdx+Rt+F
这里提醒大家,我们需要习惯于这种数学模型的表述。如何习惯?简单!长期接触长期体味,逐渐地,你就体会到这种简单方法的奇妙和快捷沟通,那么,该方程是到底什么意思呢?
2.1 牛顿力学
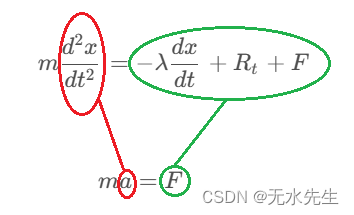
我i们知道牛顿公式
m
a
=
F
ma = F
ma=F
只要对这个方程任意加入能解释的项就可以了,大致的框架如下图:
其中:
d
2
x
d
t
2
\frac{d^2x}{dt^2}
dt2d2x:加速度,是位移对时间的二阶导。
−
λ
d
x
d
t
-\lambda \frac{dx}{dt}
−λdtdx: 该项是运动阻力,速度越大,阻力越大,因此成正比。
R
t
R_t
Rt:是个力,来自高斯随机过程。
F
F
F:是个外力,可有可无。
其实,几乎所有的宏观物理方程框架来自牛顿,而且,框架类似,细节不同。
随机力
R
t
R_t
Rt是一个
δ
\delta
δ相关的平稳高斯过程,其均值和方差如下:
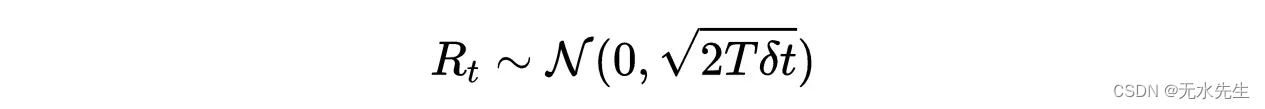
术语“
δ
\delta
δ相关”意味着两个不同时间的力是零相关的。 Langevin方程是第一个描述不平衡热力学的数学方程。
2.2 流体中的随机运动
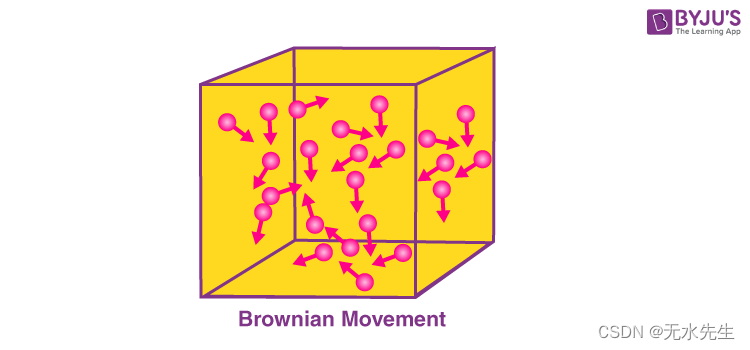
什么是布朗运动?
“布朗运动是指悬浮在流体中的小颗粒所表现出的随机运动。它通常被称为“布朗运动”。这种运动是粒子与流体中其他快速移动的粒子碰撞的结果。
布朗运动以苏格兰植物学家罗伯特·布朗的名字命名,他首先观察到花粉粒放入水中时会沿随机方向移动。下面提供了描述流体粒子的随机运动(由这些粒子之间的碰撞引起)的图示。
三、小质量物体布朗运动方程
先参考朗之万方程:
m
d
2
x
d
t
2
=
−
λ
d
x
d
t
+
R
t
+
F
m \frac{d^2x}{dt^2}=-\lambda\frac{dx}{dt}+R_t + F
mdt2d2x=−λdtdx+Rt+F
当
m
<
ε
m<\varepsilon
m<ε
表示:如果粒子的质量足够小,我们可以把左边设为零。此外,我们可以用某个势能的导数来表示一个(保守)力,比如引力。我们得到:
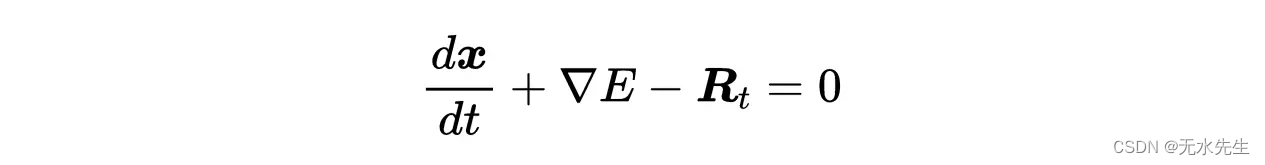
小质量的朗之万方程
写作:
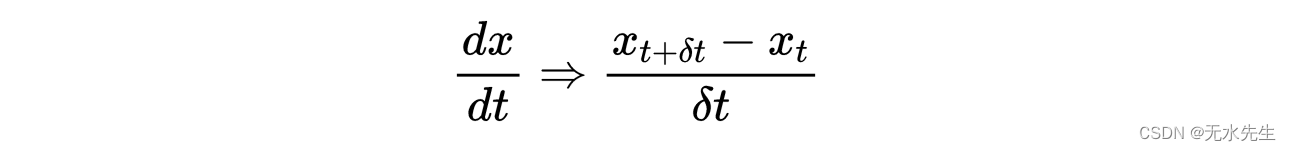
其中δt是一个小时间间隔,并有移动项,我们得到了小质量粒子的离散朗之万方程:
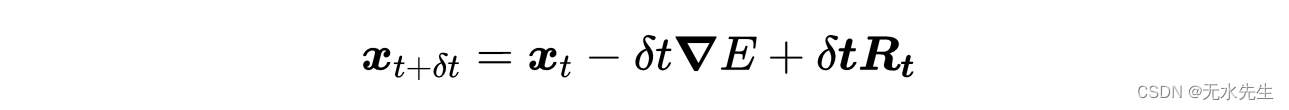
用这种方式表示,朗之万方程描述了经历布朗运动的粒子的增量位移。至此,我们可以用计算机程序实现整个过程。
四、布朗运动的Python代码
为了模拟二维离散布朗过程,采用了两种一维过程。步骤如下:
首先,选择时间步数“steps”。
坐标x和y是随机跳跃的累积和(函数np.cumsum()用于计算它们)。
中间点X和Y通过使用np.interp()插值计算。
然后使用plot()函数绘制布朗运动。
代码是:
import numpy as np
import matplotlib.pyplot as plt
import random
steps =5000
random.seed(42)
x,y = np.cumsum(np.random.randn(steps)), np.cumsum(np.random.randn(steps))
points = 10
ip = lambda x, steps, points: np.interp(np.arange(steps*points),np.arange(steps)*points,x)
X, Y = ip(x, steps, points), ip(y, steps, points)
fig, ax = plt.subplots(1, 1, figsize=(10, 10))
ax.set_title('Brownian Motion')
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.plot(X, Y, color='green',marker='o', markersize=1)
plt.show()
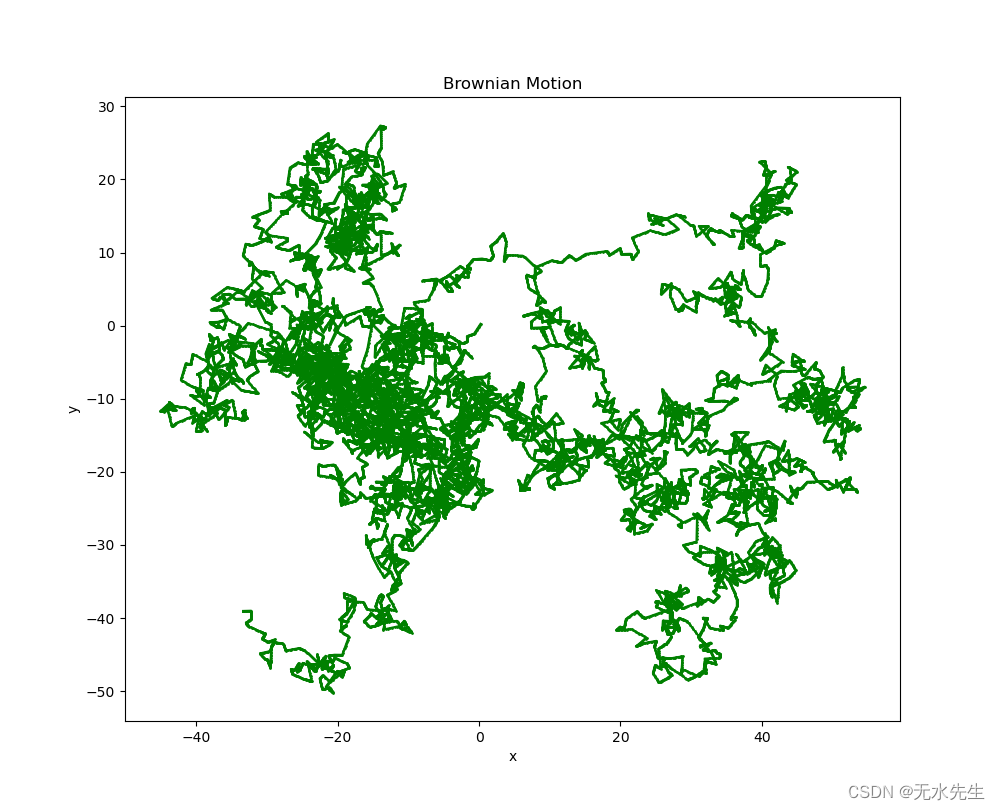
五、稳定性讨论
布朗运动图解
朗之万动力学与全局极小值
朗之万动力学的一个重要性质是随机过程x(t)(其中x(t)服从上面给出的Langevin方程)的扩散分布p(x)收敛于平稳分布,即普遍存在的波尔兹曼分布(BD)。
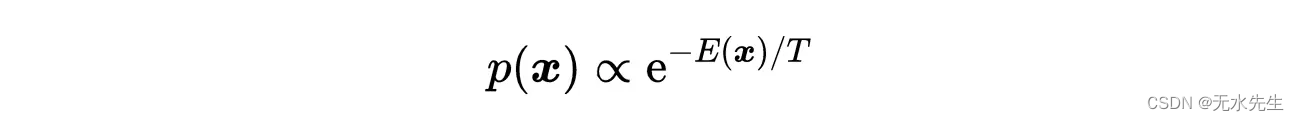
5.1 波尔兹曼分布
它集中在势能E(x)的全局最小值附近(从它的函数形式,我们可以很容易地看到BD峰在势能E(x)的全局最小值上)。更准确地说,如果温度按照离散步骤缓慢降至零:
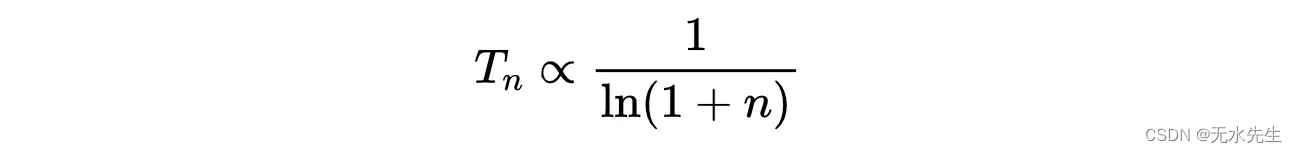
那么p(x)在n的大值时收敛于玻尔兹曼分布(x收敛于E(x)的全局最小值)。朗之万方程的时变温度通常被解释为描述亚稳态物理状态的衰减到系统的基态(这是能量的全局最小值)。因此,我们可以使用朗之万动力学来设计算法,使其成为潜在非凸函数的全局最小化。
这一原理是模拟退火技术的基础,用于获得近似的全局最优函数。模拟退火在寻找极大值中的应用。
5.2 梯度下降算法
现在我将转到机器学习优化算法。
梯度下降是一个简单的迭代优化算法最小化(或最大化)函数。在机器学习的背景下,这些函数是损失函数。为具体起见,考虑一个多元损失函数L(w),定义了一些不动点p周围的所有点w。GD算法基于一个简单的性质,即从任何点p开始,函数L(w)在其负梯度方向上衰减最快:
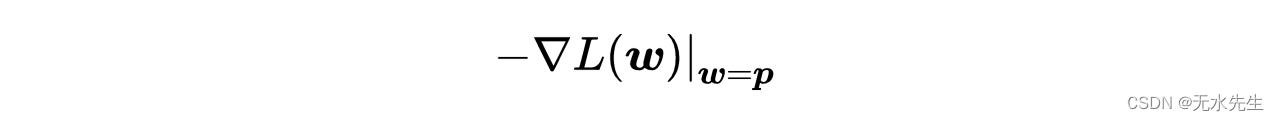
损失函数的负梯度。
人们首先猜测最小值的初始值,然后计算序列:
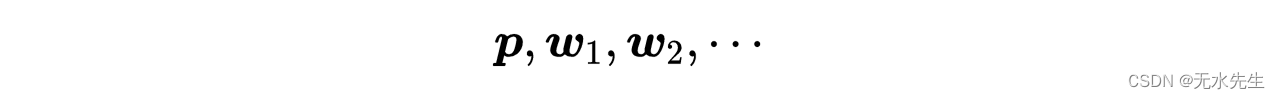
遵循迭代过程:
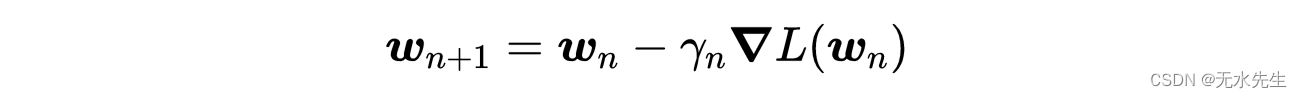
梯度下降法递归。
其中,γ为学习率,允许在每次迭代n时改变学习率。如果损失函数L及其梯度具有一定的性质,按照一定的协议选择学习率变化,保证局部收敛(只有当L是凸函数时才保证收敛到全局最小值,因为对于凸函数,任何局部最小值也是全局最小值)。
六、随机梯度下降(SGD)和小批量梯度下降
基本的GD算法在每次迭代时都扫描完整的数据集,而SGD和小批量GD只使用训练数据的一个子集。SGD在每次迭代中使用单个训练数据样本更新梯度,即在扫描训练数据时,对每个训练示例执行上述w的更新。小批量GD使用小批量的训练示例执行参数更新。
让我们用数学的方式来解释。用于一般训练集:
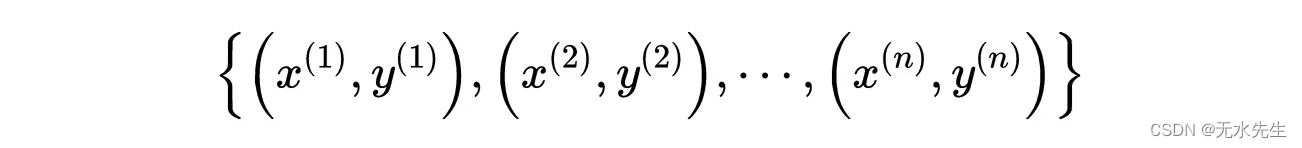
n个样本的训练集。
损失函数的一般形式为:
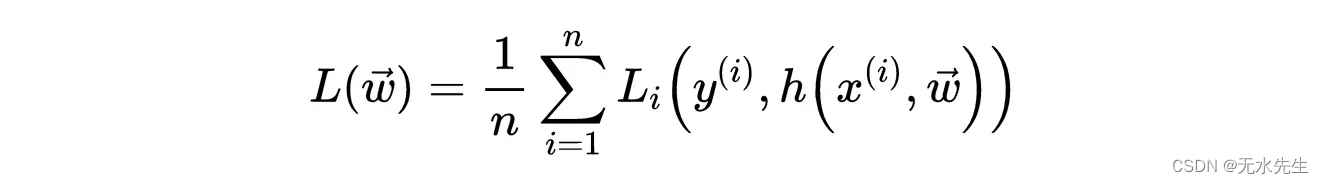
一般损失函数。
在小批梯度下降的情况下,总和仅在批内的训练示例。特别是SGD只使用一个样本。与普通的GD相比,这些过程有两个主要优势:它们速度更快,并且可以处理更大的数据集。
定义G和g如下所示,在这种情况下我们有:
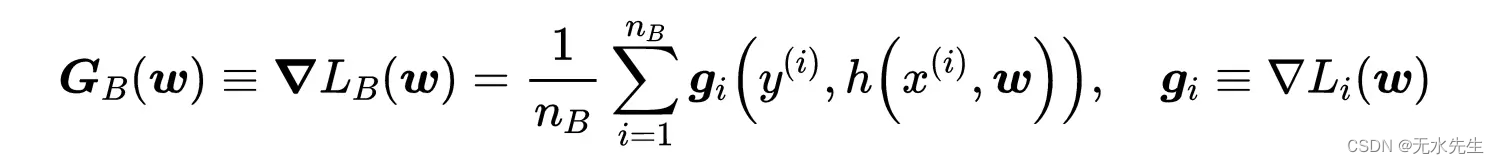
在下面的动画中,SGD的收敛和其他方法一起展示了(这些其他方法,本文没有提到,是SGD的最新改进)。
七、机器学习与物理,作为朗之万过程的梯度下降
下一个步骤对于论证是至关重要的。为了让读者理解主要思想,我省略了一些较为严格的细节。
我们可以把小批量梯度写成全梯度和正态分布的η之间的和:
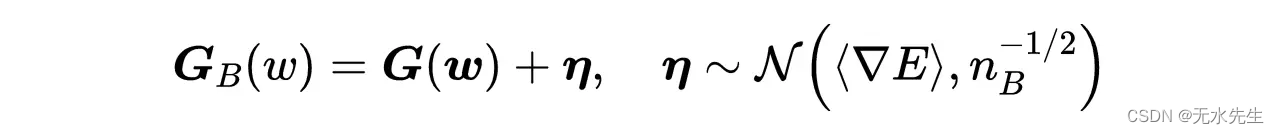
现在将这个表达式代入GD迭代表达式中,我们得到:
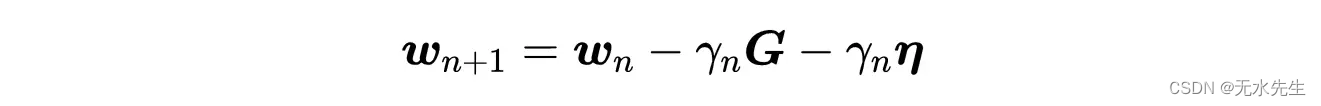
小批量梯度下降迭代步骤
一个优雅的联系
将小批量梯度下降迭代的表达式与朗之万方程进行比较,我们可以立即注意到它们的相似性。更准确地说,它们通过以下方式变得相同:

用γ代入δt,我们发现:
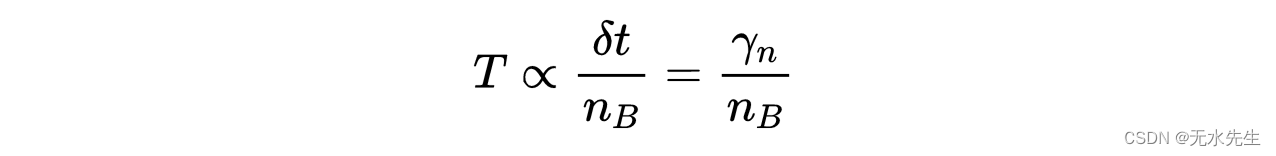
因此,SGD或小批量梯度下降算法形式上类似于朗之万过程,这就解释了为什么如果学习率按照前面提到的协议变化,它们有非常高的概率选择全局最小值。
这个结果并不新鲜。事实上,有许多证据表明,在通常的梯度下降递归中添加一个噪声项会使算法收敛到全局最小值。
结论
在这篇文章中,我展示了将随机或小批量梯度下降看作是朗之万随机过程,并通过学习率包括额外的随机化级别,我们可以理解为什么这些算法可以作为全局优化器工作得如此好。这是一个很好的结果,它表明从多个角度检查一个问题通常是非常有用的。

![练习14 Web [极客大挑战 2019]Upload](https://img-blog.csdnimg.cn/direct/8cbc3da0411f4b15873e2fbdc27e2c3e.png)





![Vue 样式技巧总结与整理[中级局]](https://img-blog.csdnimg.cn/direct/2ef7d9e8907246a9bafaec9197eaaedb.png)