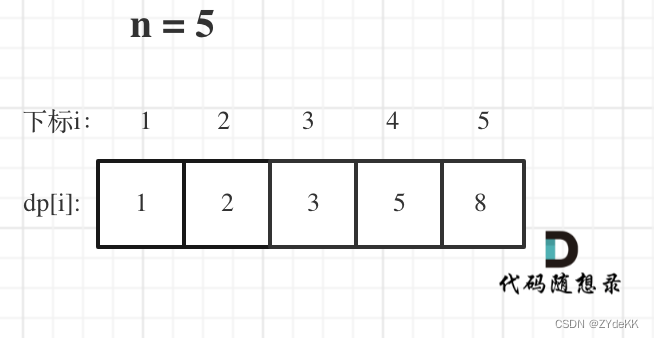
509.斐波那契数列

动规五步曲：

1. 确定 dp[i] 含义：第 i 个斐波那契数值为 dp[i]
2. 递推公式：dp[i] = dp[i - 1] + dp[i - 2]
3. dp数组初始化：dp[0] = dp[1] = 1
4. 遍历顺序：从前向后
5. 打印dp数组

class Solution:
    def fib(self, n: int) -> int:
        # 如果 n==0，
        # 那么dp会被初始化为1个元素长，
        # 导致初始化前2个元素的时候报错。
        if n == 0:
            return 0
        dp = [0] * (n + 1)  # n 表示 第 n+1 个斐波那契数（可以自己写一个数列数一数）
        dp[0], dp[1] = 0, 1
        # 循环从 第3个 数开始，第n+1个 数结束
        # 也就是说，下标从 2 开始，n 结束
        for i in range(2, n + 1):
            dp[i] = dp[i - 1] + dp[i - 2]

        return dp[n]

70.爬楼梯

1阶：1种：1台阶

2阶：2种：1台阶2次；2台阶1次

3阶：3种：1台阶3次；1台阶1次+2台阶1次；2台阶1次+1台阶2次

对于3阶，可以从1阶或者2阶爬1次到达，也就是说3阶 = 1阶 + 2阶 = 1 + 2 = 3。

动规五步曲：

1. 确定 dp[i] 含义：爬到第 i 阶台阶有 dp[i] 种方法
2. 递推公式：dp[i] = dp[i - 1] + dp[i - 2]
3. dp数组初始化：dp[1] = 1, dp[2] = 2（本题要求 n > 0）
4. 遍历顺序：从前到后
5. 打印dp数组

class Solution:
    def climbStairs(self, n: int) -> int:
        if n == 1:
            return 1
        dp = [0] * (n + 1)
        dp[1] = 1
        dp[2] = 2

        for i in range(3, n+1):
            dp[i] = dp[i - 1] + dp[i - 2]
        return dp[n]

746.使用最小花费爬楼梯

动规五步曲：

1. 确定 dp[i] 含义：爬到第 i 阶台阶需要的花费为 dp[i]
2. 递推公式：dp[i] = min(dp[i - 1] + cost[i - 1], dp[i - 2] + cost[i - 2])。到达 dp[i] 有两种方法（从dp[i - 1]跨1步，或者从dp[i - 2]跨2步），两者花费不同，我们选择最小花费。
3. dp数组初始化：dp[0] = 0, dp[0] = 0。题意表示我们可以自由选择从下标为 0 或下标为 1 的台阶开始爬楼梯。从某台阶开始是不需要花费的，而攀爬需要花费。
4. 遍历顺序：从前到后
5. 打印dp数组

class Solution:
    def minCostClimbingStairs(self, cost: List[int]) -> int:
        # 需要注意的是，根据题意，顶楼为台阶数+1
        dp = [0] * (len(cost) + 1)
        dp[0], dp[1] = 0, 0
        
        for i in range(2, len(cost) + 1):
            dp[i] = min(dp[i-1]+cost[i-1], dp[i-2]+cost[i-2])

        return dp[-1]