题目与题解
参考资料:回溯总结
332.重新安排行程
题目链接:332.重新安排行程
代码随想录题解:332.重新安排行程
视频讲解:带你学透回溯算法(理论篇)| 回溯法精讲!_哔哩哔哩_bilibili
解题思路:
这题有两个难点,一个是要求返回的结果是按升序排列最小的,另一个是行程要保证使用每一张机票,并且假设机票行程存在环路,不能困在环中。
针对第一个难点,可以提前对tickets进行排序,利用list.sort方法重写其中的comparator,排序的key为tickets里面每一张ticket的目的地,也就是tickets.get(i).get(1),这样保证有结果时,第一个结果一定是升序最小。
针对第二个难点,这里是树枝的去重问题,所以可以用一个usedTickets数组,记录每一张ticket的使用情况,用过就设置为true,保证不会重复使用。
然后就可以用回溯三部曲:
参数有 - 用于存放结果的result,用于记录路线的path,输入tickets,usedTickets数组和每次递归时的起点start(这里也可以不需要这个参数,用path.getLast()代替)
终止条件 - 题目要求每张机票都使用,那么每有N张机票,途径地点就有N+1个,所以当path的元素到达n+1后,路径就完成了,可以返回结果。
单层遍历逻辑:循环遍历tickets里面的每一个元素,如果usedTickets[i]为true,或者tickets.get(i).get(1) 不等于start,则跳过该循环;否则将tickets.get(i).get(1)加入path,usedTickets[i]设置为true,调用回溯方法,修改start为tickets.get(i).get(1),出来后修改usedTickets[i]为false并弹出path最后一个元素即可。
class Solution {
List<String> result = new ArrayList<>();
LinkedList<String> path = new LinkedList<>();
public List<String> findItinerary(List<List<String>> tickets) {
boolean[] usedTickets = new boolean[tickets.size()];
// tickets.sort((list1, list2) -> list1.get(0).compareTo(list2.get(0)));
tickets.sort(Comparator.comparing(list -> list.get(1)));
path.add("JFK");
findItinerary(tickets, usedTickets, "JFK");
return result;
}
boolean findItinerary(List<List<String>> tickets, boolean[] usedTickets, String start) {
if (path.size() == tickets.size() + 1) {
result = new ArrayList<>(path);
return true;
}
for (int i = 0; i < tickets.size(); i++) {
if (usedTickets[i] || !tickets.get(i).get(0).equals(start)) continue;
path.add(tickets.get(i).get(1));
usedTickets[i] = true;
if (findItinerary(tickets, usedTickets, tickets.get(i).get(1)))
return true;
usedTickets[i] = false;
path.pollLast();
}
return false;
}
}但是这样写在leetcode上不能ac,会提示超时,因为每次遍历tickets都是从头开始遍历的,搜索效率非常低,需要用map替代list。
看完代码随想录之后的想法
随想录答案改造了一下ticket,用Map<String, Map<String, Integer>> map存储tickets每一个起点对应的多个目的地,以及机票用过与否的情况。目前自己写还比较难,先放着以后看。
class Solution {
private Deque<String> res;
private Map<String, Map<String, Integer>> map;
private boolean backTracking(int ticketNum){
if(res.size() == ticketNum + 1){
return true;
}
String last = res.getLast();
if(map.containsKey(last)){//防止出现null
for(Map.Entry<String, Integer> target : map.get(last).entrySet()){
int count = target.getValue();
if(count > 0){
res.add(target.getKey());
target.setValue(count - 1);
if(backTracking(ticketNum)) return true;
res.removeLast();
target.setValue(count);
}
}
}
return false;
}
public List<String> findItinerary(List<List<String>> tickets) {
map = new HashMap<String, Map<String, Integer>>();
res = new LinkedList<>();
for(List<String> t : tickets){
Map<String, Integer> temp;
if(map.containsKey(t.get(0))){
temp = map.get(t.get(0));
temp.put(t.get(1), temp.getOrDefault(t.get(1), 0) + 1);
}else{
temp = new TreeMap<>();//升序Map
temp.put(t.get(1), 1);
}
map.put(t.get(0), temp);
}
res.add("JFK");
backTracking(tickets.size());
return new ArrayList<>(res);
}
}遇到的困难
想了一个多小时,超时问题实在不知道怎么解,hard不愧是hard。
51. N皇后
题目链接:51. N皇后
代码随想录题解:51. N皇后
视频讲解:这就是传说中的N皇后? 回溯算法安排!| LeetCode:51.N皇后_哔哩哔哩_bilibili
解题思路:
两眼一麻黑,直接抄答案。
看完代码随想录之后的想法
重点还是得把图画出来,理清每一层的思路,才能真正写出来。
首先来看一下皇后们的约束条件:
- 不能同行
- 不能同列
- 不能同斜线
确定完约束条件,来看看究竟要怎么去搜索皇后们的位置,这里可以抽象为一棵树。
用一个 3 * 3 的棋盘,将搜索过程抽象为一棵树,如图:
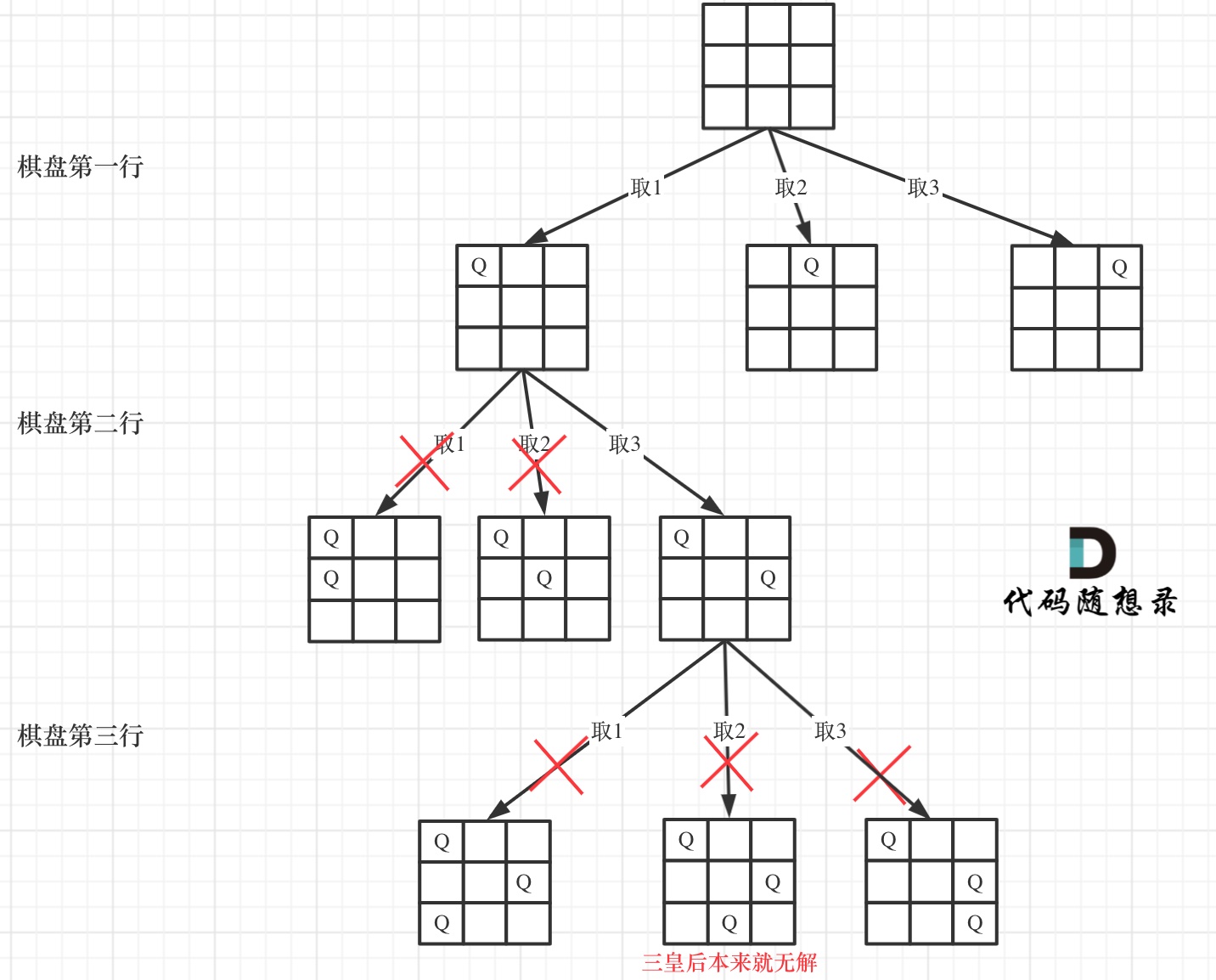
从图中,可以看出,二维矩阵中矩阵的高就是这棵树的高度,矩阵的宽就是树形结构中每一个节点的宽度。
那么我们用皇后们的约束条件,来回溯搜索这棵树,只要搜索到了树的叶子节点,说明就找到了皇后们的合理位置了
递归函数参数:定义全局变量二维数组result来记录最终结果,参数n是棋盘的大小,然后用row来记录当前遍历到棋盘的第几层了。
终止条件:当递归到棋盘最底层(也就是叶子节点)的时候,就可以收集结果并返回了,此时row=n
单层搜索的逻辑:递归深度就是row控制棋盘的行,每一层里for循环的col控制棋盘的列,一行一列,确定了放置皇后的位置。每次都是要从新的一行的起始位置开始搜,所以都是从0开始。
验证棋盘是否合法:按照如下标准去重:
- 不能同行,这里不需要检查,因为每次递归必然是换新的一行
- 不能同列
- 不能同斜线 (45度和135度角),这里注意超过180度的对角不用考虑,因为按递归的顺序,大于row的行里面不会有棋子。
class Solution {
List<List<String>> result = new ArrayList<>();
List<String> path = new ArrayList<>();
public List<List<String>> solveNQueens(int n) {
char[][] chessboard = new char[n][n];
for (int i = 0; i < n; i++) {
Arrays.fill(chessboard[i], '.');
}
solveNQueens(n, 0, chessboard);
return result;
}
void solveNQueens(int n, int row, char[][] chessboard) {
if (row == n) {
List<String> temp= new ArrayList<>();
for (int i = 0; i < n; i++) {
temp.add(String.copyValueOf(chessboard[i]));
}
result.add(temp);
return;
}
for (int i = 0; i < n; i++) {
if (!isValid(chessboard, i, row, n)) continue;
chessboard[row][i] = 'Q';
solveNQueens(n, row+1, chessboard);
chessboard[row][i] = '.';
}
}
boolean isValid(char[][] chessboard, int col, int row, int n) {
for (int i = 0; i < n; i++) {
if (chessboard[i][col] == 'Q')
return false;
}
for (int i = 1; col - i >= 0 && row - i >= 0 ; i++) {
if (chessboard[row - i][col - i] == 'Q')
return false;
}
for (int i = 1; col + i < n && row - i >= 0 ; i++) {
if (chessboard[row - i][col + i] == 'Q')
return false;
}
return true;
}
}遇到的困难
一开始连N皇后问题的定义都不是很清楚,就抓瞎了,这种特型的二维数组题以后就有参考标准了。
37. 解数独
题目链接:37. 解数独
代码随想录题解:37. 解数独
视频讲解:回溯算法二维递归?解数独不过如此!| LeetCode:37. 解数独_哔哩哔哩_bilibili
解题思路:
见答案,二刷再看
看完代码随想录之后的想法
遇到的困难
今日收获
今天全是hard题,确实很难,二刷再好好看。
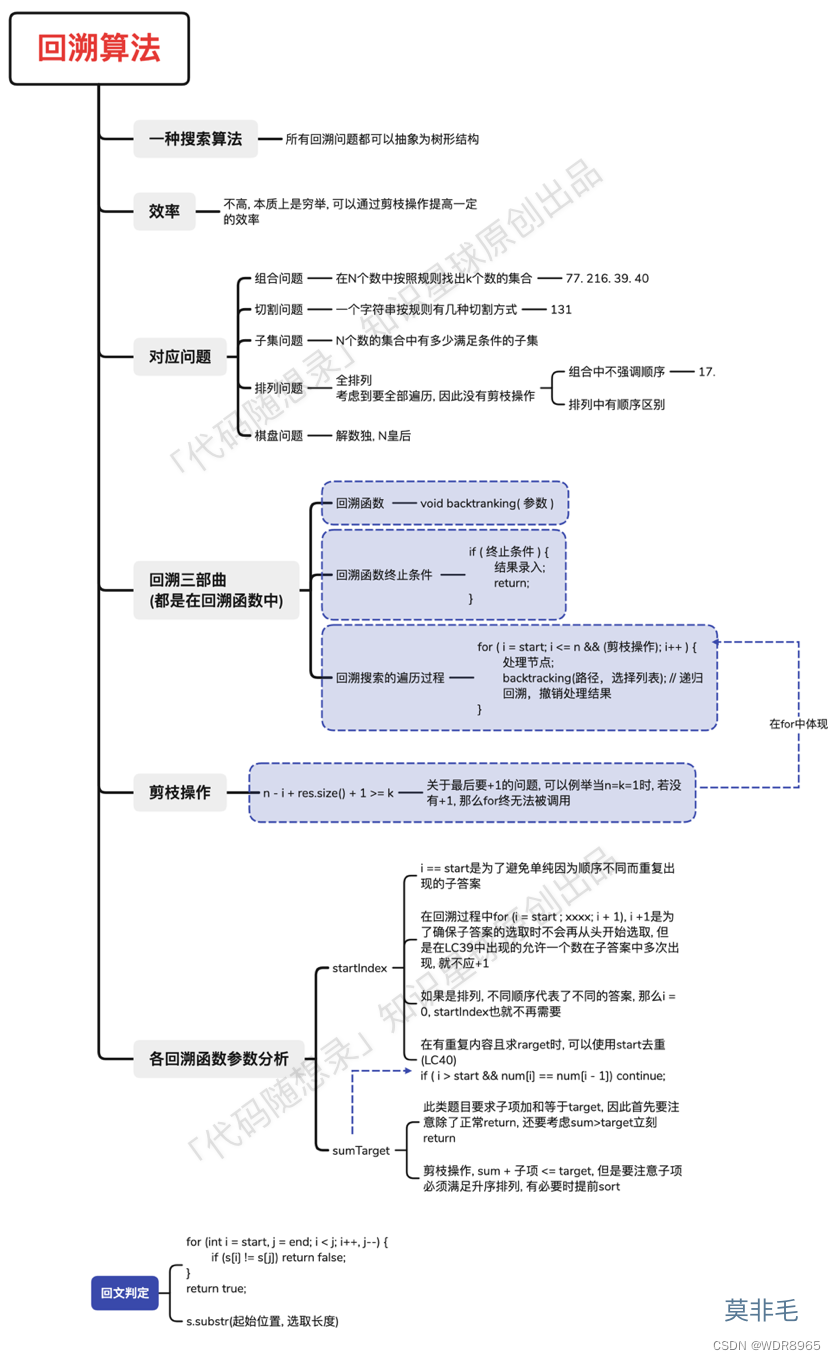
回溯总结:
回溯算法能解决如下问题:
- 组合问题:N个数里面按一定规则找出k个数的集合
- 排列问题:N个数按一定规则全排列,有几种排列方式
- 切割问题:一个字符串按一定规则有几种切割方式
- 子集问题:一个N个数的集合里有多少符合条件的子集
- 棋盘问题:N皇后,解数独等等
在树形结构中子集问题是要收集所有节点的结果,而组合问题是收集叶子节点的结果。
对于组合问题,for循环在寻找起点的时候要有一个范围,如果这个起点到集合终止之间的元素已经不够题目要求的k个元素了,就没有必要搜索了
排列问题与组合的不同:
- 每层都是从0开始搜索而不是startIndex
- 需要used数组记录path里都放了哪些元素了
去重:使用set去重的版本相对于used数组的版本效率都要低很多