题目描述
数轴上有n个闭区间:D1,...,Dn。
其中区间Di用一对整数[ai, bi]来描述,满足ai < bi。
已知这些区间的长度之和至少有10000。
所以,通过适当的移动这些区间,你总可以使得他们的“并”覆盖[0, 10000]——也就是说[0, 10000]这个区间内的每一个点都落于至少一个区间内。
你希望找一个移动方法,使得位移差最大的那个区间的位移量最小。
具体来说,假设你将Di移动到[ai+ci, bi+ci]这个位置。你希望使得maxi{|ci|} 最小。输入
输入的第一行包含一个整数n,表示区间的数量。
接下来有n行,每行2个整数ai, bi,以一个空格分开,表示区间[ai, bi]。
保证区间的长度之和至少是10000。输出
输出一个数字,表示答案。如果答案是整数,只输出整数部分。如果答案不是整数,输出时四舍五入保留一位小数。
样例输入
2
10 5010
4980 9980
样例输出20
首先说思路,在满足条件的所有值中取最大值,常见的二分问题,而又涉及到区间遍历,可能会有考贪心。这道题,大致看起来,可以按一般贪心的思路,将全部区间按右端点值由小到大排序,然后采用二分,判断mid值是否可以让所有区间通过移位达到连续不断,并且长度大于10000。
①二分:这道题看数据会出现小数,其实最小也就0.5,我看别人的做法是把有关区间以及距离什么的都乘2,这样算出来的mid最小值也就为1,可以用整数二分。但我直接用的实数二分,也是差不多的,可能算的次数会多一点。
②check函数:每次二分,都要判断mid是否满足条件,就要用到check函数。其实我的想法是遍历区间,拿遍历到的某个区间[l,r]跟之前遍历完所有区间形成的右端最大值mr比较,如果l-mid>mr,那说明我往左移也跟前面所有区间形成不了交集,那当然后边的区间也一样,所以直接判断mid不符合要求(当时是这样想的,不过细想其实有错),然后就这样遍历完,如果mr≥10000,不就说明mid可以实现区间移位连续嘛,那就继续二分,直到二分的区间缩成一个值。
但是,最后程序无论怎么改,都只过了九个测试点,挠头
(过九个测试点):
#include<bits/stdc++.h>
using namespace std;
struct Point{
int l,r;
Point(int a,int b){
l=a,r=b;
}
friend bool operator<(const Point& p1,const Point& p2){
if(p1.r!=p2.r)return p1.r<p2.r;//为什么要优先用r排序?贪心思想,
else return p1.l<p2.l;
}
};
vector<Point>pv;
bool check(double mid){
cout<<mid<<endl;
vector<Point>temp(pv);//复制vector来进行模拟
double mr=0;//表示所有区间通过不同移动能将右端点扩大到的范围
for(int i=0;i<temp.size();i++){
int l=temp[i].l,r=temp[i].r;
if(mr+1e-6>l-mid&&mr<r+mid+1e-6){
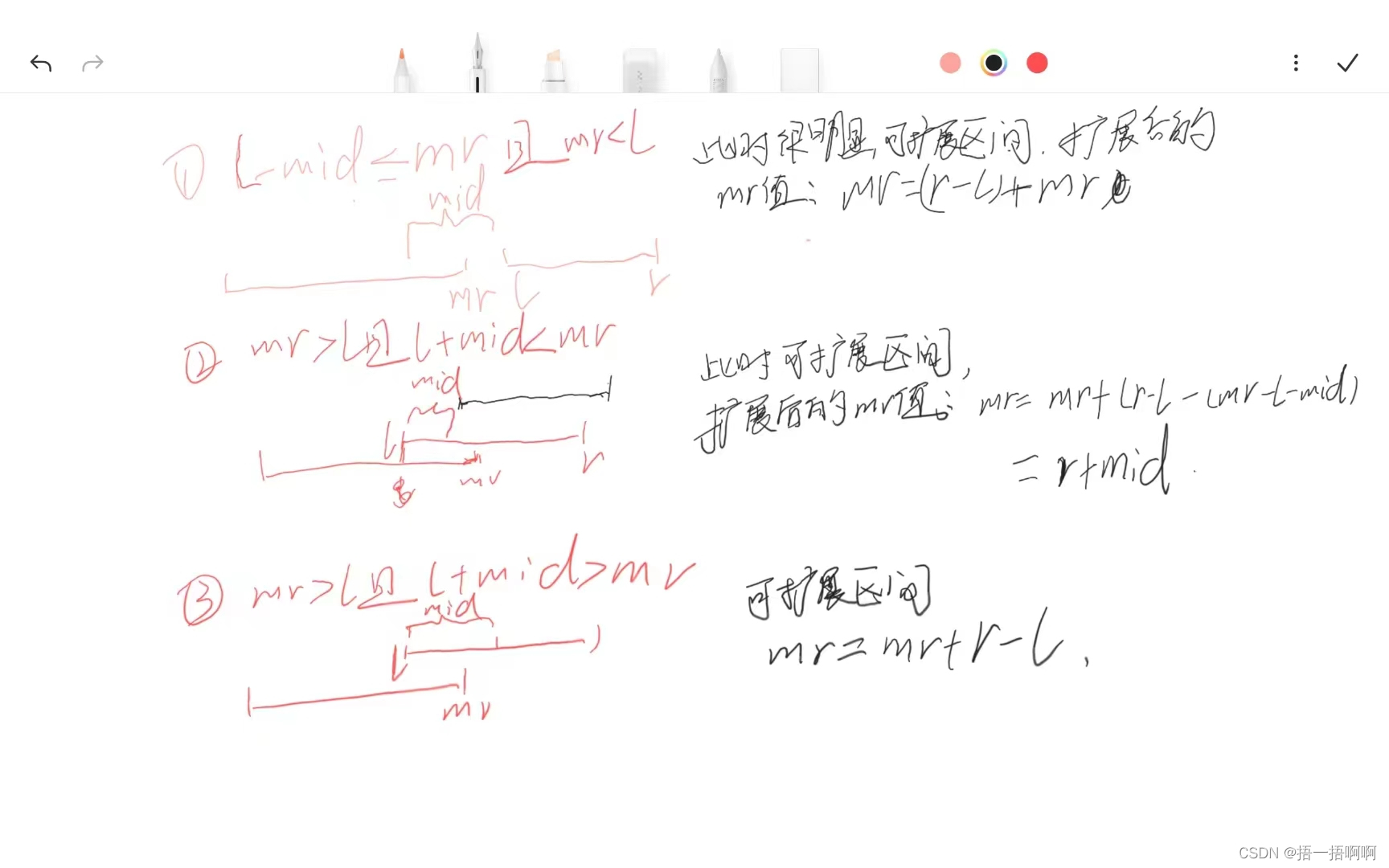
//mr>=l-mid说明可以通过对区间[l,r]进行左移操作实现与原来的区间有交,也就是使整个区间连续,mr<=r+mid是指通过这个区间[l,r]右移,可以实现mr变大,不然处理[l,r]区间又有什么意义呢
if(mr<l){
mr=r-l+mr;
}else{
if(l+mid>mr)mr+=(r-l);
else mr+=(r-l-(mr-l-mid));
}
}
if(mr<l-mid)return false;
}
return mr+1e-6>10000;//循环正常结束也不一定能行,要区间右端最大值大于等于10^4
}
int main(){//这道题,典型的大于中找最小,大于是指mid超过某一个值,就可以实现所有区间移动覆盖整个范围,最小是指要找的mid要满足条件且最小,直接套模板
int n;
cin>>n;
int l,r;
for(int i=0;i<n;i++){
cin>>l>>r;
pv.push_back(Point(l,r));
}
sort(pv.begin(),pv.end());
double L=0,R=10000,mid;
while(R-L>1e-6){
cout<<mid<<" "<<L<<" "<<R<<endl;
mid=(L+R)/2;//维护左边
if(check(mid)){
R=mid;
}else{
L=mid;
}
}
if(mid>1e-6)cout<<mid<<endl;
else cout<<0<<endl;
}好吧,现在讲讲AC的代码,我当时看别人的题解也好奇,为什么一次遍历的事,他还要加个while循环,这不增加工作量嘛,我绞尽脑汁也想不明白while有什么用处,后边才发现,原来是弥补贪心策略的不足!!!我先举个例子:
对于数据 :
3
1000 2000
800 3000
2200 10000
考虑贪心,区间按右端点值从小到大排吗?这样输出的答案可不对哦,输出的答案会是1000,正确的答案可是800!!!
那要不考虑区间按左端点从大到小排?
对于数据:
3
2 1000
3 8
1002 1000
按左排输出的答案可就是994了喔!!!所以,我自己也不知道到底要怎样贪心了
可能ac的人也不知道吧,所以他们添了一层循环,为的是保证一个之前没用到的区间,以后还有机会用,这样就加大了正确的可能,毕竟,谁也不知道哪个区间先用上嘛,不同区间用的先后次序不同,可能产生不同结果。
自我安慰:这道题主要考二分,其他不懂的是次要的(好吧,还是自己贪心不行)![]()
所以,要是有更好的策略,可以跟我分享,救救菜狗![]()
(叠甲,这篇博客是在精神不正常状态下写的,语无伦次,看题解可以去那些大佬博客)
(AC):
#include<bits/stdc++.h>
using namespace std;
struct Point{
int l,r;
Point(int a,int b){
l=a,r=b;
}
friend bool operator<(const Point& p1,const Point& p2){
if(p1.r!=p2.r)return p1.r<p2.r;//为什么要优先用r排序?贪心思想,
else return p1.l<p2.l;
}
};
vector<Point>pv;
bool check(double mid){
vector<Point>temp(pv);//复制vector来进行模拟
double mr=0;//表示所有区间通过不同移动能将右端点扩大到的范围
while(true){//避免一些特殊区间影响,弥补贪心的不足
bool flag=false;
for(int i=0;i<temp.size();i++){
int l=temp[i].l,r=temp[i].r;
if(mr+1e-6>l-mid&&mr<r+mid+1e-6){
//mr>=l-mid说明可以通过对区间[l,r]进行左移操作实现与原来的区间有交,也就是使整个区间连续,mr<=r+mid是指通过这个区间[l,r]右移,可以实现mr变大,不然处理[l,r]区间又有什么意义呢
flag=true;
if(mr<l){
mr=r-l+mr;
}else{
if(l+mid>mr)mr+=(r-l);
else mr+=(r-l-(mr-l-mid));
}
temp.erase(temp.begin()+i);
break;
}
}
if(!flag||mr+1e-6>10000)break;
}
return mr+1e-6>10000;//循环正常结束也不一定能行,要区间右端最大值大于等于10^4
}
int main(){//这道题,典型的大于中找最小,大于是指mid超过某一个值,就可以实现所有区间移动覆盖整个范围,最小是指要找的mid要满足条件且最小,直接套模板
int n;
cin>>n;
int l,r;
for(int i=0;i<n;i++){
cin>>l>>r;
pv.push_back(Point(l,r));
}
sort(pv.begin(),pv.end());
double L=0,R=10000,mid;
while(R-L>1e-6){
mid=(L+R)/2;//维护左边
if(check(mid)){
R=mid;
}else{
L=mid;
}
}
if(mid>1e-6)cout<<mid<<endl;
else cout<<0<<endl;
}