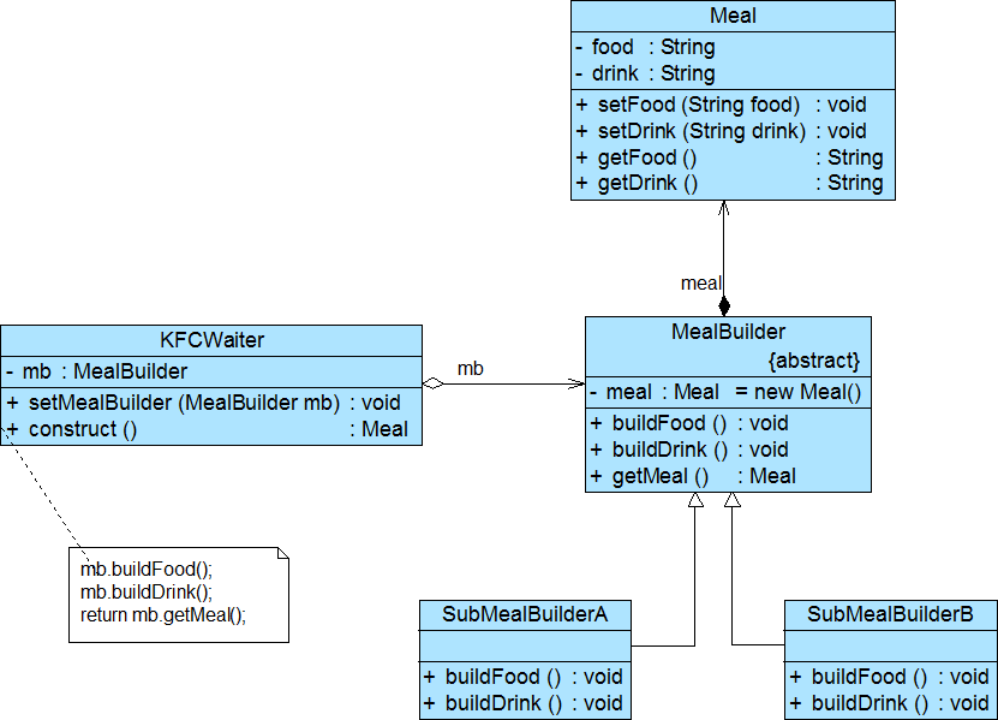
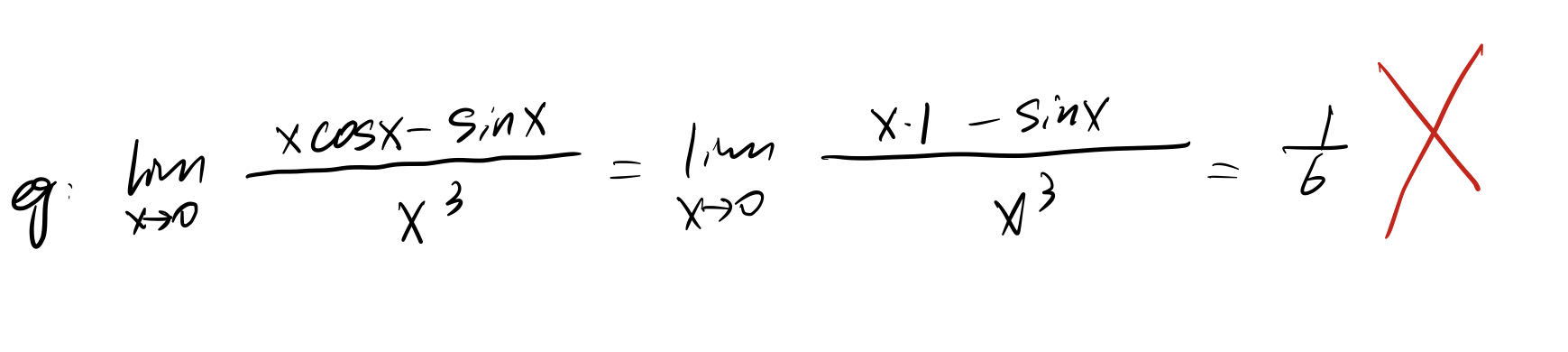就直接从算法部分开始了:
2 算法
我们的目标是定义一个前向(或者推理)扩散过程,这个过程能够转换任意的复杂数据分部到一个简单、tractable、分布,并且学习有限时间扩散过程的反转 从而 定义我们的生成模型分布。我们接着展示了反转、生成式扩散过程能够被训练,并且被用来评估可能性。我们同样推导出这些反转过程的交叉熵界,并且展示怎么学习分布能够被第二个分布相乘(例如,在修复货去噪图像时,计算后验所做的那样)。
2.1 前向轨迹
我们标记了数据分布 . 数据的分布逐渐转换为一个表现优异(也叫 tractable,应该是可控的意思)的分布
通过重复应用马尔可夫扩散内核
对于
,其中
是扩散概率,
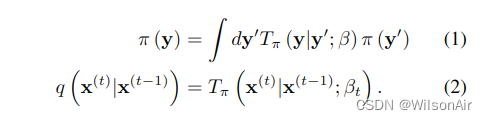
因此,对应于从数据分布开始并执行 T 步扩散的前向轨迹是
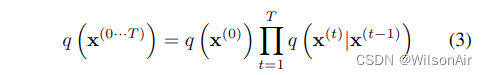
对于如下所示的实验,对应于高斯扩散到具有恒等协方差的高斯分布,或二项式扩散到独立的二项式分布。表 App.1 给出了高斯分布和二项式分布的扩散核。

表App.1。针对高斯和二项扩散过程的具体情况,本文的关键方程。N (u; μ, Σ) 是均值 μ 和协方差 Σ 的高斯分布。B (u; r) 是单个伯努利试验的分布,u = 1 以概率 r 出现,u = 0 以概率 1 - r 出现。最后,对于扰动伯努利试验b^t i = x(t-1)(1-\beta_t) + 0.5\beta_t, c^t i =[f_b(x(t+1), t)]i, dt i = r(x(t)i = 1),对于单个位i给出分布。
2.2 反向轨迹
生成分布将被训练来描述相同的轨迹,但相反,
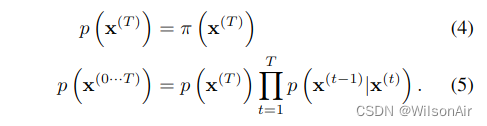
对于高斯扩散和二项式扩散,对于连续扩散(小步长 β 的极限),扩散过程的反转具有与正向过程相同的函数形式(Feller,1949)。由于 是一个高斯(二项式)分布,如果 β_t 很小,则
也将是一个高斯(二项式)分布。轨迹越长,扩散速率β越小。
在学习过程中,只需要估计高斯扩散核的均值和协方差,或二项式核的位翻转概率。如表App.1所示,
- f_μ(x^(t),t)和f_Σ(x^(t),t)是定义高斯反向马尔可夫跃迁的均值和协方差的函数,
- f_b(x^(t),t)是提供二项分布的位翻转概率的函数。
运行该算法的计算成本是这些函数的成本,乘以时间步的数量。对于本文中的所有结果都,多层感知器用于定义这些函数。然而,广泛的回归或函数拟合技术将适用,包括非参数方法。
2.3. 模型概率
生成模型分配给数据的概率为
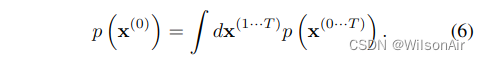
天真地这个积分是难以处理的——但从退火重要性采样和 Jazynski 等式中获取线索,我们改为评估正向和反向轨迹的相对概率,平均在前向轨迹上,
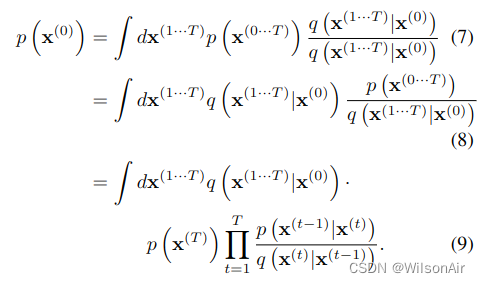
这可以通过平均来自前向轨迹 q (x(1···T )|x(0)) 的样本来快速评估。对于无穷小的 β,轨迹上的正向和反向分布可以是相同的(参见第 2.2 节)。如果它们相同,则只需要来自 q (x(1···T )|x(0)) 的单个样本来准确评估上述积分,这可以通过替换看到。这对应于统计物理学中准静态过程的情况(Spinney & Ford,2013;Jarzynski,2011)。
2.4 训练
训练相当于最大化模型对数似然,
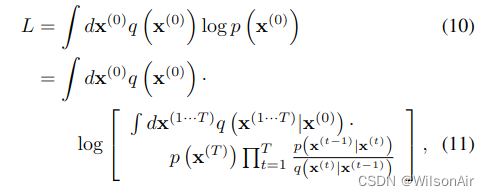
其下界由Jensen不等式提供,
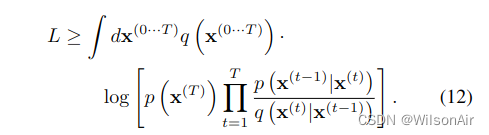
如附录 B 中所述,对于我们的扩散轨迹,这减少到,
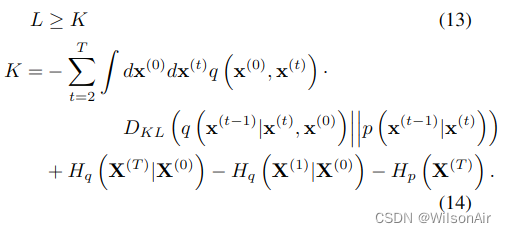
其中熵和 KL 散度可以解析计算。这个界限的推导平行于变分贝叶斯方法中对数似然界的推导。
如第 2.3 节所述,如果正向和反向轨迹相同,对应于准静态过程,则等式 13 中的不等式变为等式。
训练包括找到最大化对数似然这个下限的反向马尔可夫转换,
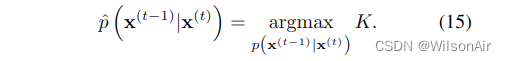
高斯扩散和二项扩散的估计具体目标如表App.1所示。
因此,估计概率分布的任务被简化为对设置高斯序列的均值和协方差的函数进行回归的任务(或设置伯努利试验序列的状态翻转概率)。
2.4.1。设置扩散RATE βt
正向轨迹中βt的选择对训练模型的性能很重要。在AIS中,中间分布的正确调度可以大大提高对数分区函数估计的准确性(Grosse et al., 2013)。在热力学中,平衡分布之间移动时所采取的时间表决定了自由能的损失程度(Spinney & Ford, 2013;Jarzynski, 2011)。
在高斯扩散的情况下,我们通过对 K 的梯度上升来学习前向扩散调度 β2···T。第一步的方差 β1 固定为一个小常数以防止过度拟合。使用“冻结噪声”明确来自 q (x(1···T )|x(0)) 的样本对 β1···T 的依赖性——如 (Kingma & Welling, 2013) 所示,噪声被视为一个额外的辅助变量,并在计算 K 相对于参数的偏导数时保持不变。
对于二项式扩散,离散状态空间使得冻结噪声的梯度上升是不可能的。相反,我们选择正向扩散计划β1···T来擦除每个扩散步骤原始信号的恒定分数1T,产生的扩散速率。
2.5. 乘法分布和计算后验
诸如计算后验以进行信号去噪或缺失值推断等任务需要将模型分布 p (x(0)) 与第二个分布或有界正函数 r (x(0)) 相乘,产生一个新的分布 ̃p (x(0)) ∝ p (x(0)) r (x(0))。
对于许多技术,包括变分自动编码器、GSNs、NDE 和大多数图形模型,乘法分布是昂贵的和困难的。然而,在扩散模型下,它很简单,因为第二个分布可以被视为扩散过程中每一步的小扰动,或者通常精确地乘以每个扩散步骤。图 3 和图 5 展示了使用扩散模型对自然图像进行去噪和修复。以下部分描述了如何在扩散概率模型的背景下乘以分布。
2.5.1。MODIFIED MARGINAL DistributionS
First,为了计算 ̃p (x(0)),我们将每个中间分布乘以相应的函数器 (x(t))。我们在分布或马尔可夫转换之上使用波浪线来表示它属于以这种方式修改的轨迹。̃p (x(0···T )) 是修改后的反向轨迹,它从分布 ̃p (x(T )) =1 ̃ZTp (x(T )) r (x(T )) 开始,并通过中间分布序列进行
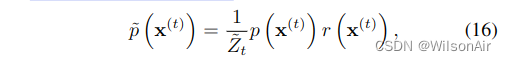
其中 ̃Zt 是第 t 个中间分布的归一化常数。
2.5.2. MODIFIED DIFFUSION STEPS
反向扩散过程的马尔可夫核p (x(t) | x(t+1))服从平衡条件
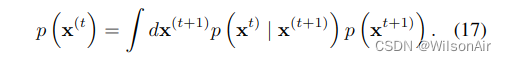
我们希望扰动马尔可夫核 ̃p (x(t) | x(t+1)) 服从扰动分布的平衡条件,
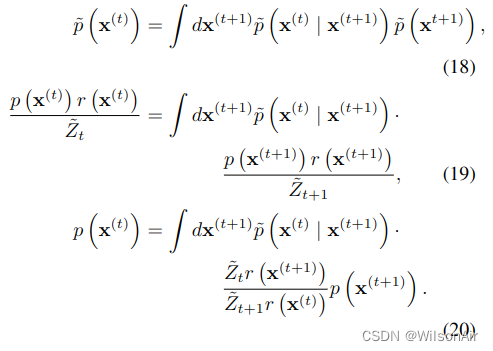
如果
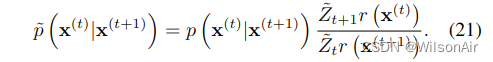
等式 20 将满足
等式 21 可能不对应于归一化概率分布,因此我们选择 ̃p (x(t)|x(t+1)) 为相应的归一化分布
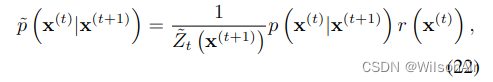
其中 ̃Zt(x(t+1)) 是归一化常数。对于高斯,由于方差小,每个扩散步骤相对于 r (x(t)) 通常是非常尖锐的峰值。这意味着 r(x(t))r(x(t+1)) 可以被视为对 p (x(t)|x(t+1)) 的微小扰动。对高斯的微小扰动会影响平均值,而不是归一化常数,因此在这种情况下,等式 21 和 22 是等价的(见附录 C)。
2.5.3. APPLYING r (x(t))
如果 r (x(t))) 足够平滑,则可以将其视为对反向扩散核 p (x(t)|x(t+1)) 的微小扰动。在这种情况下,̃p (x(t)|x(t+1)) 将具有与 p (x(t)|x(t+1)) 相同的函数形式,但对高斯核具有扰动均值,或二项式核的扰动翻转率。扰动扩散核在表App.1中给出,并在附录C中导出高斯。
如果 r (x(t))) 可以以封闭形式与高斯(或二项式)分布相乘,则可以直接以封闭形式与反向扩散核 p (x(t)|x(t+1)) 相乘。这适用于 r (x(t))) 由某些坐标子集的 delta 函数组成的情况,如图 5 中的修复示例所示。
2.5.4. CHOOSING r (x(t))
通常,应该选择 r (x(t)) 在轨迹过程中缓慢变化。对于本文中的实验,我们选择它是恒定的,
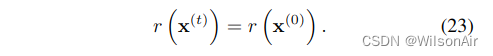
另一个方便的选择是 r (x(t)) = r (x(0)) T -t T。在此第二种选择 r (x(t))) 对反向轨迹的起始分布没有贡献。这保证了从 ̃p (x(T )) 中抽取初始样本以进行反向轨迹仍然很简单。
2.6.反向过程的熵
由于正向过程是已知的,我们可以推导出反向轨迹中每一步条件熵的上界和下界,从而推导出对数似然,
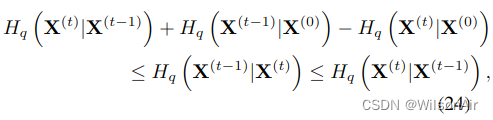
其中上界和下界都仅取决于q (x(1···T)|x(0)),并且可以解析计算。推导在附录 A 中提供。