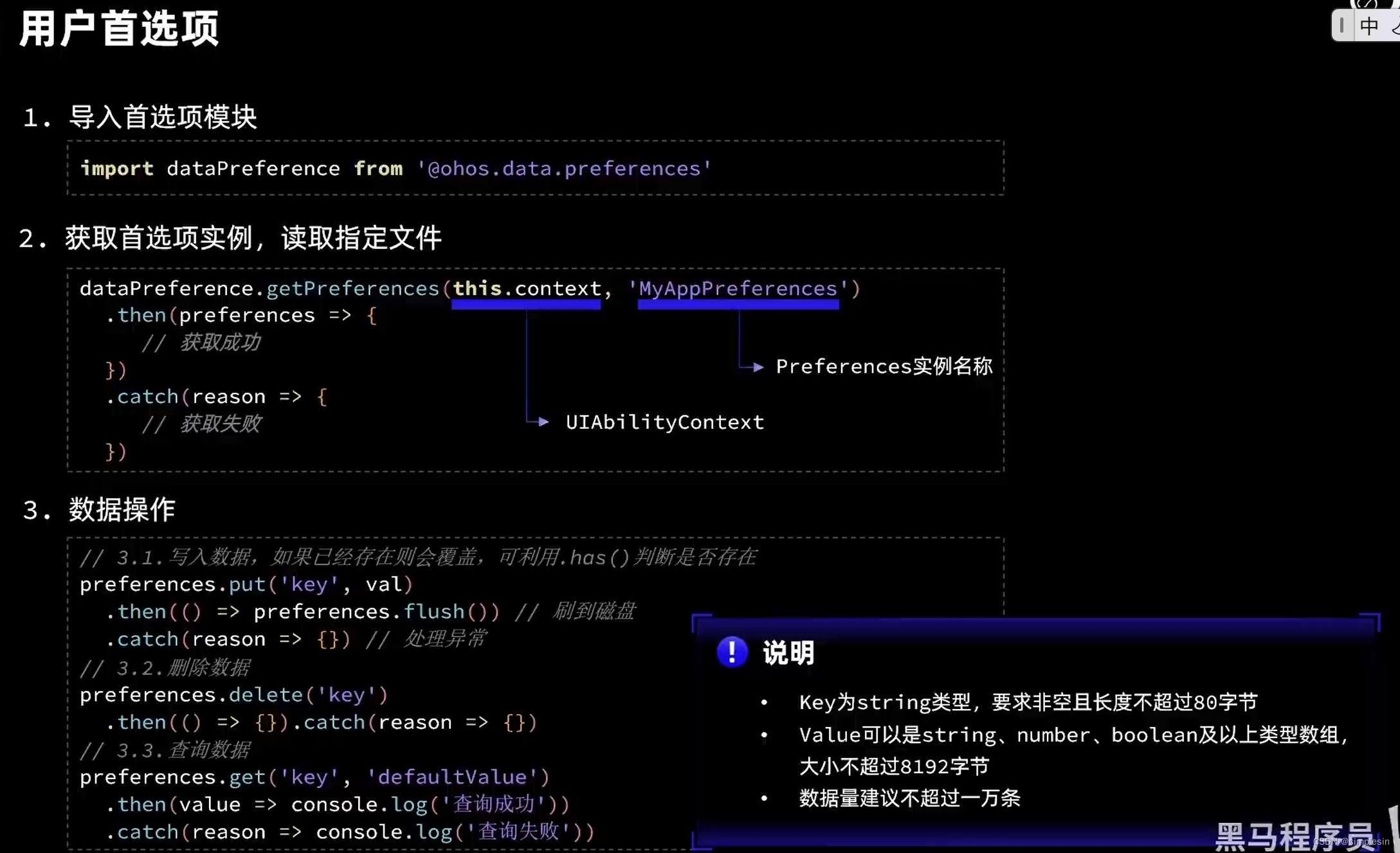
蓝桥集训之垒骰子

• 核心思想：矩阵乘法

  • 

  • f[i]存顶面数值 构造a矩阵 使得*f[i] = f[i-1]a

  • 则f[i] = f[1] * aⁿ

    • 快速幂优化

•   #include <iostream>
    #include <cstring>
    #include <algorithm>
    
    using namespace std;
    typedef long long LL;
    const int N = 6,mod = 1e9+7;
    
    int a[N][N];
    int n,m;
    
    void mul(int c[][N], int a[][N], int b[][N])
    { 
        static int t[N][N];  //缓存c答案数组
        memset(t, 0, sizeof t);
        for (int i = 0; i < 6; i ++ )
            for (int j = 0; j < 6; j ++ )
                for (int k = 0; k < 6; k ++ )
                    t[i][j] = (t[i][j] + (LL)a[i][k] * b[k][j]) % mod;
    
        memcpy(c, t, sizeof t);
    }
    int get_op(int x)
    {
        if(x>=3) return x-3;  //找对应的排斥元素的顶面
        return x+3;
    }
    int main()
    {
        cin>>n>>m;
        for(int i=0;i<N;i++)
            for(int j=0;j<N;j++)
                a[i][j] = 4;  //顶面确定 旁边四个面可以交换 一共4种方案
        while(m--)
        {
            int x,y;
            cin>>x>>y;
            x--,y--;
            a[x][get_op(y)] = a[y][get_op(x)] = 0;  //排斥的一对置0
        }
        int f[N][N] = {4,4,4,4,4,4};
        //将f一维矩阵写成二维矩阵 下面全是0的形式
        //mul函数只写一个就可以了
        for(int k=n-1;k;k>>=1)  //快速幂
        {
            if(k&1) mul(f,f,a);
            mul(a,a,a);
        }
        int res=0;
        for(int i=0;i<N;i++) res = (res+f[0][i]) %mod;  //f[0][i]最终存个数
        cout<<res<<endl;
        return 0;
    }