1. 整数在内存中的存储
在计算机系统中,数值⼀律⽤补码来表⽰和存储。原因在于,使⽤补码,可以将符号位和数值域统⼀处理;同时,加法和减法也可以统⼀处理(CPU只有加法器)此外,补码与原码相互转换,其运算过程是相同的,不需要额外的硬件电路。
2. ⼤⼩端字节序和字节序判断
#include <stdio.h>
int main()
{
int a = 0x11223344;
return 0;
}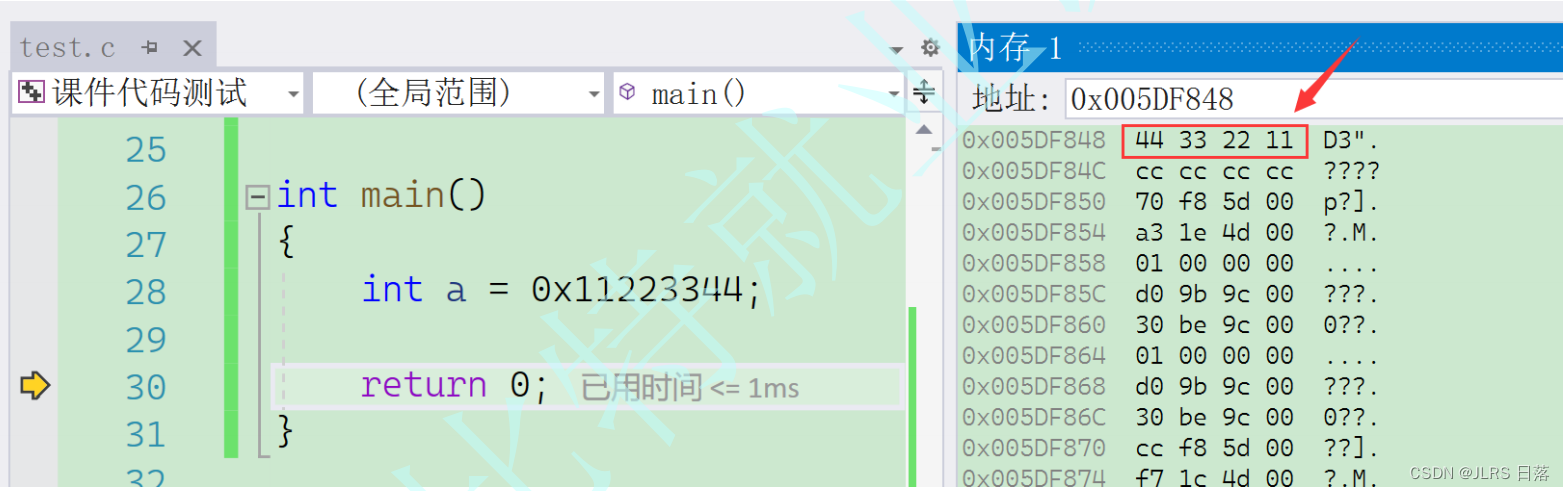
2.1 什么是⼤⼩端?
是指数据的低位字节内容保存在内存的⾼地址处,⽽数据的⾼位字节内容,保存在内存的低地址处。
⼩端(存储)模式:
是指数据的低位字节内容保存在内存的低地址处,⽽数据的⾼位字节内容,保存在内存的⾼地址处。
例如10进制中的123,1、2、3分别是百位,十位,个位,那么3就是低位。
上述概念需要记住,⽅便分辨⼤⼩端。
2.2 为什么有⼤⼩端?
2.3 练习
2.3.1 练习1
//代码1
#include <stdio.h>
int check_sys()
{
int i = 1;
return (*(char *)&i);
}
int main()
{
int ret = check_sys();
if(ret == 1)
{
printf("⼩端\n");
}
else
{
printf("⼤端\n");
}
return 0;
}解题思路:这里将&i的int*地址强制转化为(char*),而不是将int强制转化为char。
2.3.2 练习2
#include <stdio.h>
int main()
{
char a= -1;
signed char b=-1;
unsigned char c=-1;
printf("a=%d,b=%d,c=%d",a,b,c);
return 0;
}

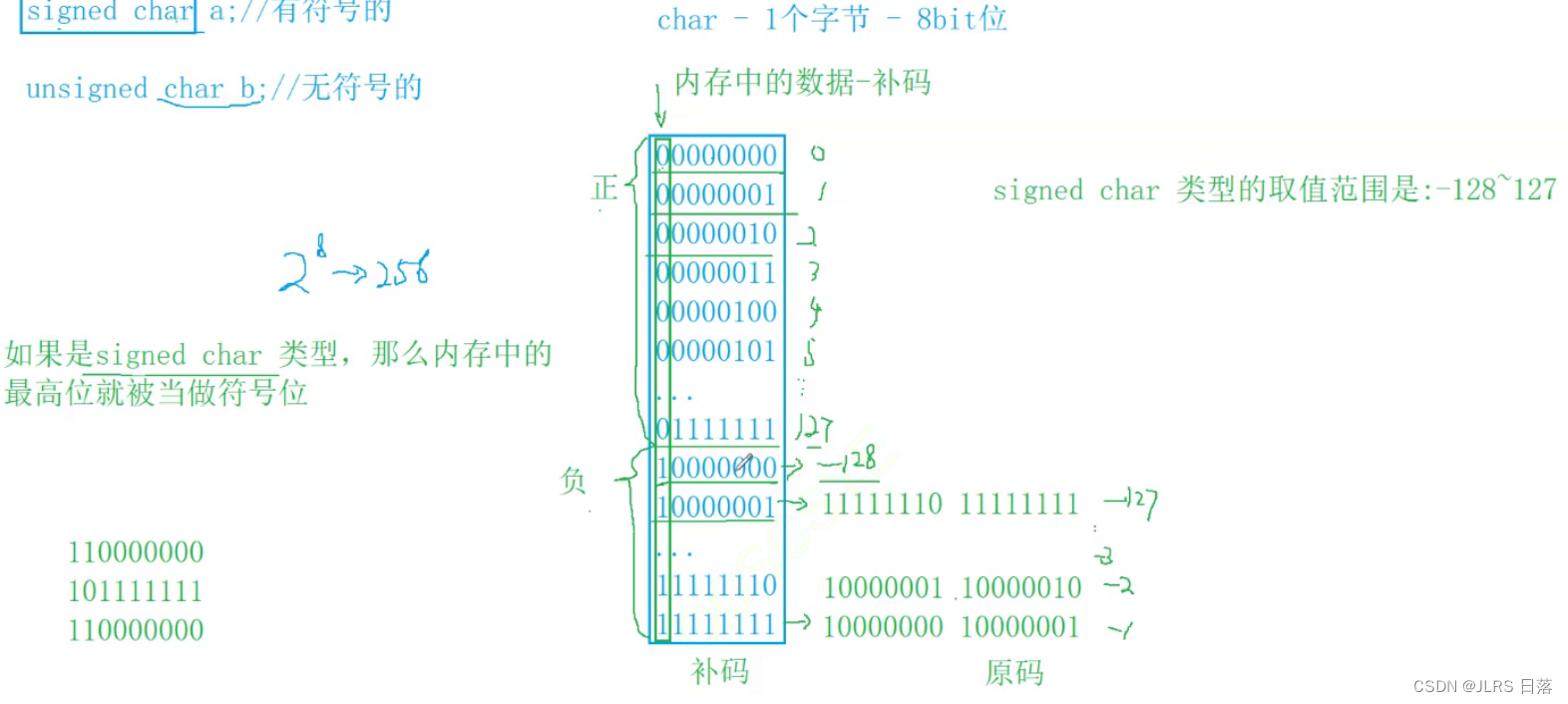

无论是否有无符号位,存入内存的都是补码,11111111,至于打印出来是什么,这时候就与signed、unsigned有关了。
%d意思就是我以有符号数的形式打印
a、b:char类型的要以%d的形式打印,需要整型提升,有符号位,那就补符号位变为11111111 11111111 11111111 11111111
补码转化为原码就是1000000...0001:-1
c:无符号位,整型提升补充0,00000....11111111,正数,原反补相同,打印结果为255
2.3.3 练习3
#include <stdio.h>
int main()
{
char a = -128;
printf("%u\n",a);
return 0;
}
这里char a = -128意思是以8个比特位的方式存储a的补码,多余的比特位不要,所以存入的是10000000,打印的时候是以%u(%u认为打印的为无符号数int,%d认为是有符号数int),先对a进行整型提升,看a的类型是char,有符号位的char,10000000的高位是符号位1,所以补符号位1,之后再打印时打印的是无符号位,打印结果为11111111 11111111 11111111 10000000的10进制
2.3.4 练习4
#include <stdio.h>
int main()
{
char a[1000];
int i;
for(i=0; i<1000; i++)
{
a[i] = -1-i;
}
printf("%d",strlen(a));
return 0;
}for循环对数组进行赋值,-1,-2...-128,由于char是有符号位,其范围为-128~127,接下来会存储
127,126.。。。

strlen求得是字符串的长度,统计的是\0(ASCII码值是0)之前的字符个数,当循环了一个周期后,输出255。
2.3.5 练习5
#include <stdio.h>
unsigned char i = 0;
int main()
{
for(i = 0;i<=255;i++)
{
printf("hello world\n");
}
return 0;
}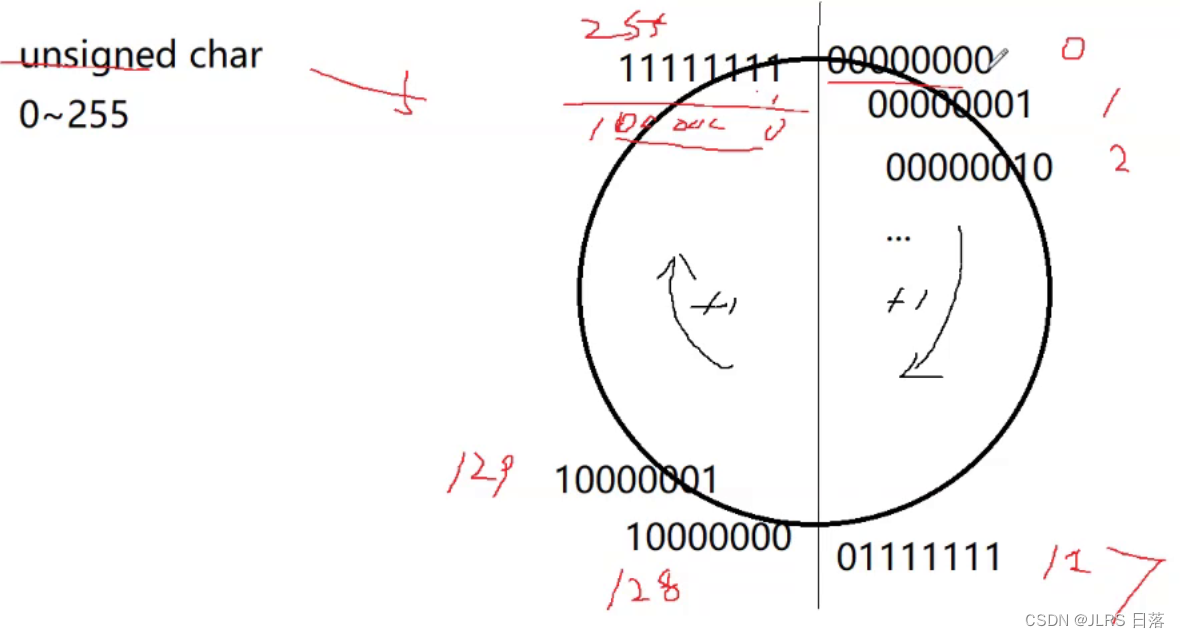
由于unsigned char类型最多储存255个,到达255后又会回到0,所以永远满足i<=255,会死循环的打印
3. 浮点数在内存中的存储
3.1 练习
#include <stdio.h>
int main()
{
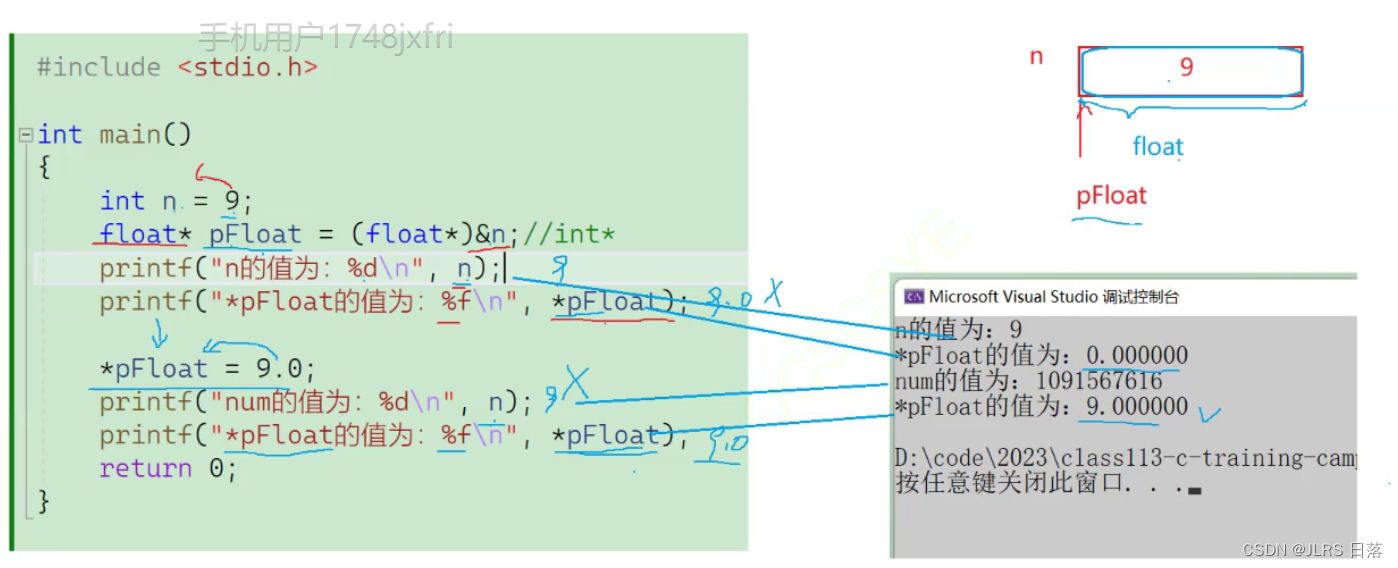
int n = 9;
float *pFloat = (float *)&n;
printf("n的值为:%d\n",n);
printf("*pFloat的值为:%f\n",*pFloat);
*pFloat = 9.0;
printf("num的值为:%d\n",n);
printf("*pFloat的值为:%f\n",*pFloat);
return 0;
}

3.2 浮点数的存储
V = (−1) ^ S ∗ M ∗ 2^ E• (−1) S 表⽰符号位,当S=0,V为正数;当S=1,V为负数• M 表⽰有效数字,M是⼤于等于1,⼩于2的• 2 E 表⽰指数位
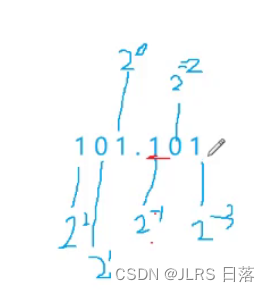

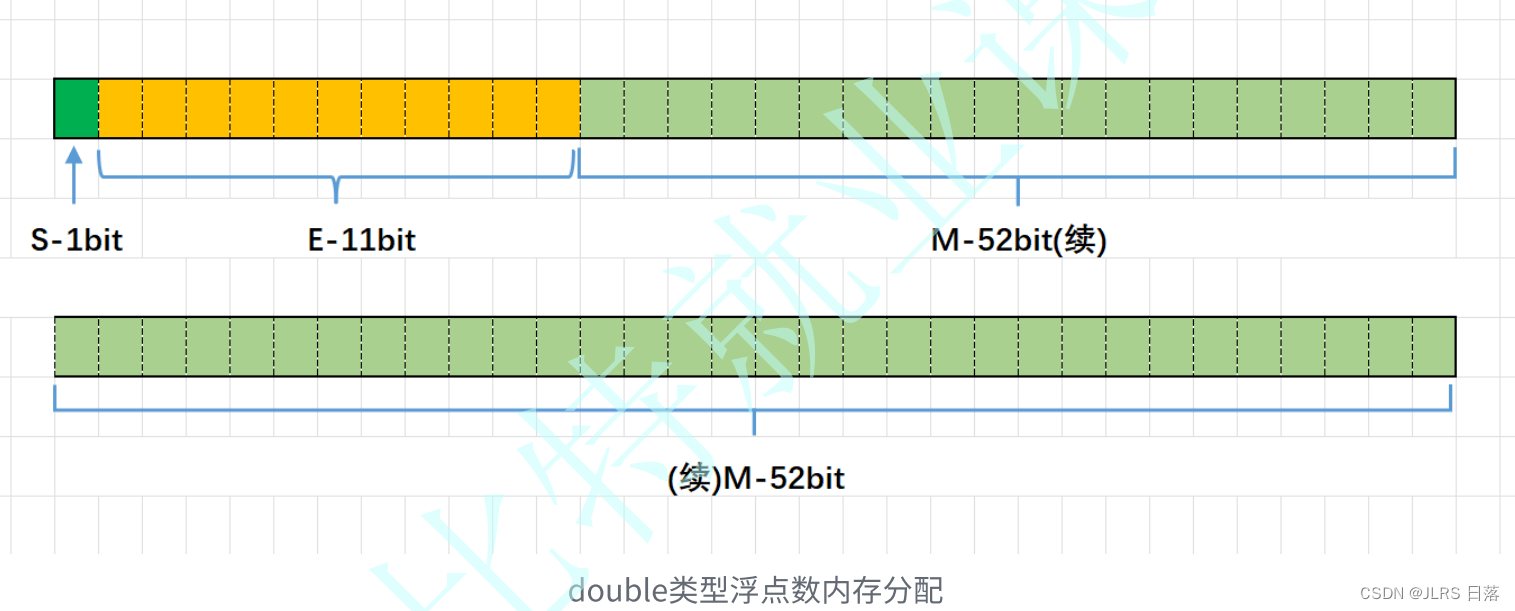
32位与64位指的是存储的bit位
3.2.1 浮点数存的过程
3.2.2 浮点数取的过程
0 01111110 00000000000000000000000
E全为0
0 00000000 00100000000000000000000


0 11111111 00010000000000000000000
与E=0同理,推出无穷大
3.3 题⽬解析


0000 0000 0000 0000 0000 0000 0000 1001
0 00000000 00000000001001S E M

9.0(10进制)
1001.0(2进制)= (-1)^0 * 1.001 * 2^3
S=0 M=001 E=3+127=130(10进制),10000010(2进制)
pFloat存入内存中则为
0 10000010 001.....(20个0)
以有符号数&d打印出
将0 10000010 001.....(20个0)转化为10进制就为结果
————————————————————————————————
完