题目描述
�N 人が円卓に座っており,各人は反時計回りに順に 1, …, �1, …, N と番号付けられています.各人はそれぞれ左右どちらか一方の利き手を持っています.
円卓上には 1, …, �1, …, N と番号付けられた計 �N 本のスプーンが,隣り合う二人の間に 11 本ずつ置いてあります.各 1 ≤ � ≤ �1 ≤ i ≤ N について,人 �i の左側,右側にはそれぞれスプーン �i,スプーン (�+1)(i+1) があります.ここで,スプーン (�+1)(N+1) はスプーン 11 のことを指します.
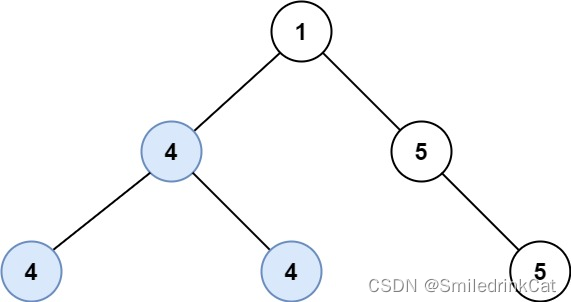
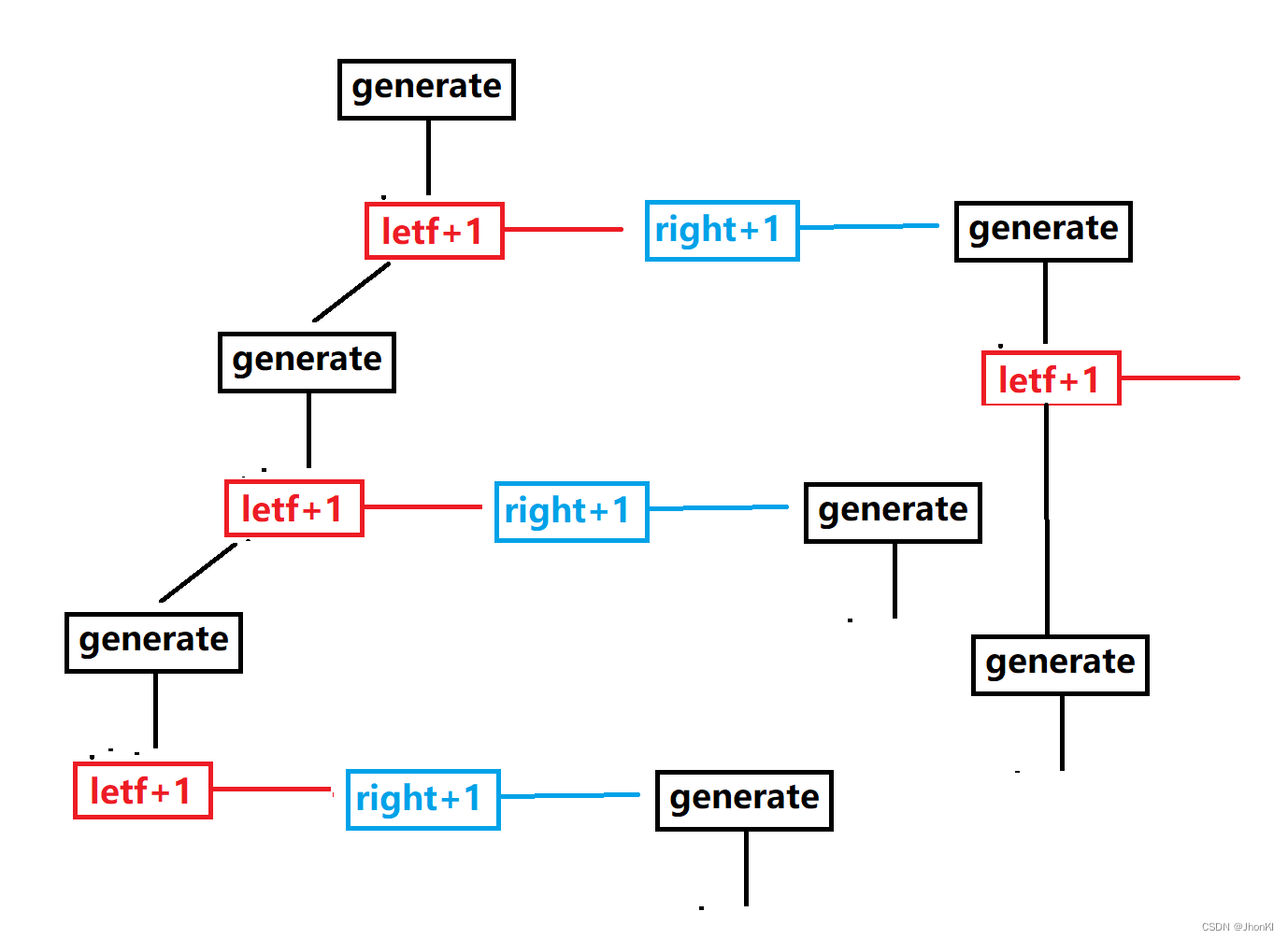
� = 4N = 4 での模式図を以下に示します.

(1, …, �)(1, …, N) の順列 (�1, …, ��)(P1, …, PN) が与えられます.�=1,…,�i=1,…,N の順に,人 ��Pi が以下のように行動します.
- 自分の右側または左側にスプーンが残っているならば,そのうち 11 つを取る.
- このとき自分の両側にスプーンが残っているならば,自分の利き手の側のスプーンを取る.
- そうでないならば何もしない.
L, R, ? からなる長さ �N の文字列 �S が与えられます.�N 人の利き手の組み合わせは 2�2N 通りありますが,そのうち以下の条件を全て満たすような組み合わせの数を 998244353998244353 で割った余りを求めてください.
- �S の �i 番目の文字が
Lならば,人 �i は左利きである. - �S の �i 番目の文字が
Rならば,人 �i は右利きである. - 全員の行動が終了したとき,全員がスプーンを取っている.
输入格式
入力は以下の形式で標準入力から与えられる.
�N �1P1 …… ��PN �S
输出格式
答えを 11 行に出力せよ.
题意翻译
问题陈述
有 �N 人围坐在一张圆桌旁,按逆时针顺序编号为 11 至 �N 。每个人都有一只优势手:左手或右手。
圆桌上有 �N 个勺子,编号从 11 到 �N ,每对相邻的人中间放一个勺子。在每个 1≤�≤�1≤i≤N 人 �i 的左边和右边,分别有勺子 �i 和 (�+1)(i+1) 。这里,勺子 (�+1)(N+1) 指的是勺子 11 。
下图是 �=4N=4 的示意图。

给定一个 (1,…,�)(1,…,N) 的排列组合 (�1,…,��)(P1,…,PN) ,这 �n 个人按照此排列的顺序行动。第 ��Pi 个人的行为如下:
- 如果左侧或右侧有剩余的勺子,他们将拿走其中一个。
- 如果两边都有剩余的勺子,他们会拿自己惯用手一边的勺子。
- 否则,他们什么也不会做。
我们还给出了一个长度为 �N 的字符串 �S ,由 L、R 和 ? 组成。在 2�2N 种可能的惯用手组合中,求有多少种满足以下所有条件,模数为 998244353998244353 :
- 如果 �S 的 �i 个字符是 "L",那么 �i 是左撇子。
- 如果 �S 的第 �i 个字符是 "R",那么 �i 就是右撇子。
- 当所有人都行动完后,每个人都拿了一个勺子。
输入输出样例
输入 #1复制
3 1 2 3 L??
输出 #1复制
2
输入 #2复制
3 1 3 2 R?L
输出 #2复制
0
输入 #3复制
12 6 2 9 3 1 4 11 5 12 10 7 8 ????????????
输出 #3复制
160
说明/提示
制約
- 入力される数値は全て整数
- 2 ≤ � ≤ 2 × 1052 ≤ N ≤ 2 × 105
- (�1, …, ��)(P1, …, PN) は (1, …, �)(1, …, N) の順列
- �S は
L,R,?からなる長さ �N の文字列
Sample Explanation 1
人 1,2,31,2,3 がそれぞれ左利き,左利き,右利きのとき,以下のように行動が行われます. - 人 11 が行動を開始する.人 11 の両側にスプーンが残っているので,人 11 の利き手と同じ左側のスプーン 11 を取る. - 人 22 が行動を開始する.人 22 の両側にスプーンが残っているので,人 22 の利き手と同じ左側のスプーン 22 を取る. - 人 33 が行動を開始する.人 33 の右側にはスプーンが残っておらず,左側にはスプーン 33 が残っているので,スプーン 33 を取る.全員の行動が終了し,このとき全員がスプーンを取っている. この利き手の組み合わせは条件を満たします.他には人 1,2,31,2,3 がそれぞれ左利き,左利き,左利きの場合も条件を満たします.
Sample Explanation 2
条件を満たす利き手の組み合わせが存在しません.
_____________________________________________________________________________
写作不易,点个赞呗!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
_____________________________________________________________________________
唉...一份超时代码:
#include <bits/stdc++.h>
using namespace std;
long long n,ans;
int a[200005];
int b[200005];//0为左1为右-1为未知
bool c[200005];//标记
string s;
bool check(){
memset(c,0,sizeof(c));
for(int i=1;i<=n;i++){
int x=a[i];
if(x!=n){
if(c[x]&&c[x+1])return false;
else if(!c[x]&&!c[x+1])c[x+b[x]]=true;
else if(!c[x])c[x]=true;
else if(!c[x+1])c[x+1]=true;
}else{
if(c[x]&&c[1])return false;
else if(!c[x]&&!c[1]){
if(b[x]==0)c[x]=true;
else c[1]=true;
}
else if(!c[x])c[x]=true;
else if(!c[1])c[1]=true;
}
}
return true;
}
void f(int x){
if(x==n+1){
if(check())ans=ans%998244353+1;
return;
}
if(b[x]==-1){
b[x]=1;
f(x+1);
b[x]=0;
f(x+1);
b[x]=-1;
}else f(x+1);
}
int main(){
cin>>n;
for(int i=1;i<=n;i++)cin>>a[i];
cin>>s;
int len=s.size();
for(int i=0;i<len;i++){
if(s[i]=='L')b[i+1]=0;
if(s[i]=='R')b[i+1]=1;
if(s[i]=='?')b[i+1]=-1;
}
f(1);
cout<<ans;
}