谷歌（Google）面试过程的第一步，你可能会收到一个在线评估链接。 评估有效期为 7 天，包含两个编码问题，需要在一小时内完成。 以下是一些供你练习的在线评估问题。

在本章结尾处，还提供了有关 Google 面试不同阶段的更多详细信息。

最长同值路径

给定一个二叉树的 root ，返回 最长的路径的长度 ，这个路径中的 每个节点具有相同值 。 这条路径可以经过也可以不经过根节点。

两个节点之间的路径长度 由它们之间的边数表示。

示例 1:

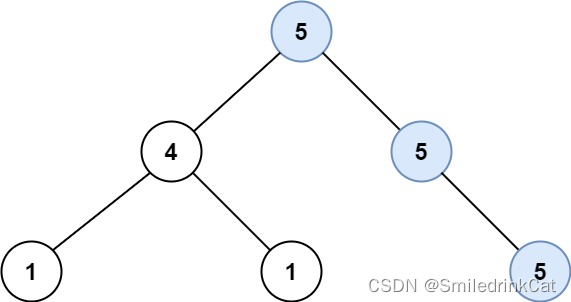
输入：root = [5,4,5,1,1,5]
输出：2

示例 2:

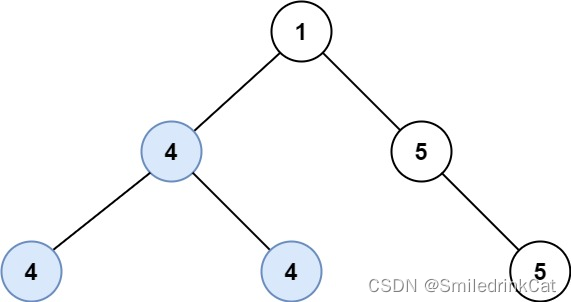
输入：root = [1,4,5,4,4,5]
输出：2

提示:

• 树的节点数的范围是 [0, 104]
• -1000 <= Node.val <= 1000
• 树的深度将不超过 1000

思路一：递归

首先，我们可以使用递归来解决这个问题。具体来说，对于每个节点，递归计算其左右子树中与当前节点值相同的路径的长度，然后返回左右子树中较长的路径长度加上当前节点的路径长度。这样就可以得到以当前节点为根节点的最长路径长度。在递归的过程中，可以用一个全局变量来记录最长的路径长度。

代码示例1：

class TreeNode:
    def __init__(self, val=0, left=None, right=None):
        self.val = val
        self.left = left
        self.right = right

class Solution:
    def longestUnivaluePath(self, root):
        self.max_length = 0

        def dfs(node):
            if not node:
                return 0
            left_length = dfs(node.left)
            right_length = dfs(node.right)
            left_arrow = right_arrow = 0
            if node.left and node.left.val == node.val:
                left_arrow = left_length + 1
            if node.right and node.right.val == node.val:
                right_arrow = right_length + 1
            self.max_length = max(self.max_length, left_arrow + right_arrow)
            return max(left_arrow, right_arrow)
        
        dfs(root)
        return self.max_length

# 示例 1
root1 = TreeNode(5)
root1.left = TreeNode(4)
root1.right = TreeNode(5)
root1.left.left = TreeNode(1)
root1.left.right = TreeNode(1)
root1.right.right = TreeNode(5)
print(Solution().longestUnivaluePath(root1)) # 输出：2

# 示例 2
root2 = TreeNode(1)
root2.left = TreeNode(4)
root2.right = TreeNode(5)
root2.left.left = TreeNode(4)
root2.left.right = TreeNode(4)
root2.right.right = TreeNode(5)
print(Solution().longestUnivaluePath(root2)) # 输出：2

这个解决方案使用了一个嵌套的辅助函数 dfs() 来递归地计算每个节点的最长路径长度。在递归的过程中，如果当前节点的值与其左子节点值或右子节点值相等，则可以从左右子树中延伸路径。然后将左右子树中较长的路径长度加上当前节点的路径长度，得到以当前节点为根节点的最长路径长度，并更新全局变量 max_length。

思路二：深度优先搜索（DFS）

第二种解决这个问题的方法是使用深度优先搜索（DFS），但稍微修改一下递归函数的返回值。在这种方法中，递归函数返回一个元组 (path_length, arrow_length)，其中 path_length 表示以当前节点为根的最长路径长度，而 arrow_length 表示从当前节点出发向左或向右延伸的最长箭头长度。然后通过不断更新全局变量 max_length 来计算最终的结果。

代码示例2：

class TreeNode:
    def __init__(self, val=0, left=None, right=None):
        self.val = val
        self.left = left
        self.right = right

class Solution:
    def longestUnivaluePath(self, root):
        self.max_length = 0

        def dfs(node):
            if not node:
                return 0, 0
            left_length, left_arrow = dfs(node.left)
            right_length, right_arrow = dfs(node.right)
            left_path = right_path = 0
            if node.left and node.left.val == node.val:
                left_path = left_length + 1
            if node.right and node.right.val == node.val:
                right_path = right_length + 1
            path_length = left_path + right_path
            arrow_length = max(left_path, right_path)
            self.max_length = max(self.max_length, path_length)
            return path_length, arrow_length

        dfs(root)
        return self.max_length

# 示例 1
root1 = TreeNode(5)
root1.left = TreeNode(4)
root1.right = TreeNode(5)
root1.left.left = TreeNode(1)
root1.left.right = TreeNode(1)
root1.right.right = TreeNode(5)
print(Solution().longestUnivaluePath(root1)) # 输出：2

# 示例 2
root2 = TreeNode(1)
root2.left = TreeNode(4)
root2.right = TreeNode(5)
root2.left.left = TreeNode(4)
root2.left.right = TreeNode(4)
root2.right.right = TreeNode(5)
print(Solution().longestUnivaluePath(root2)) # 输出：2

在这个解决方案中，递归函数 dfs() 返回一个元组 (path_length, arrow_length)，表示以当前节点为根的最长路径长度和从当前节点向左或向右延伸的最长箭头长度。在递归的过程中，通过更新全局变量 max_length 来计算最终结果。

思路三：广度优先搜索（BFS）

第三种解题思路是使用广度优先搜索（BFS），通过遍历树中的每个节点来计算最长路径。在每一步中，记录当前节点的值以及从根节点到该节点的路径长度。如果当前节点的值与其父节点的值相同，则更新当前节点的路径长度为父节点的路径长度加1，否则将当前节点的路径长度重置为1。然后根据当前节点的路径长度更新最长路径的值。这种方法遍历了树中的每个节点，时间复杂度较高，但在一些情况下可能是一种简单直观的解决方案。

代码示例3：

class TreeNode:
    def __init__(self, val=0, left=None, right=None):
        self.val = val
        self.left = left
        self.right = right

class Solution:
    def longestUnivaluePath(self, root):
        if not root:
            return 0
        queue = [(root, 1)]  # 使用队列存储节点及其路径长度
        max_length = 0
        while queue:
            node, length = queue.pop(0)
            max_length = max(max_length, length)
            if node.left:
                if node.left.val == node.val:
                    queue.append((node.left, length + 1))
                else:
                    queue.append((node.left, 1))
            if node.right:
                if node.right.val == node.val:
                    queue.append((node.right, length + 1))
                else:
                    queue.append((node.right, 1))
        return max_length

# 示例 1
root1 = TreeNode(5)
root1.left = TreeNode(4)
root1.right = TreeNode(5)
root1.left.left = TreeNode(1)
root1.left.right = TreeNode(1)
root1.right.right = TreeNode(5)
print(Solution().longestUnivaluePath(root1)) # 输出：2

# 示例 2
root2 = TreeNode(1)
root2.left = TreeNode(4)
root2.right = TreeNode(5)
root2.left.left = TreeNode(4)
root2.left.right = TreeNode(4)
root2.right.right = TreeNode(5)
print(Solution().longestUnivaluePath(root2)) # 输出：2

这个解法利用了 BFS 遍历树的每个节点，并在遍历过程中记录当前节点的值以及从根节点到该节点的路径长度。如果当前节点的值与其父节点的值相同，则更新当前节点的路径长度为父节点的路径长度加1，否则将当前节点的路径长度重置为1。最后根据当前节点的路径长度更新最长路径的值。