一、前言

二、前缀和

1、基本概念

2、前缀和与差分的关系

3、差分数组能提升修改的效率

三、例题

1、统计子矩阵（lanqiao2109，2022年省赛）

（1）处理输入

（2）方法一：纯暴力（30%）

（3）方法二：前缀和（70%）

（4）方法三：前缀和+尺取法（100%）

（5）个人拙见

2、灵能传输（lanqiaoOJ题号196）

一、前言

前缀和正如字面意思，用一个新数组把旧数组每个位置的前缀和存起来，希望下面的内容能加深大家对前缀和的理解。

二、前缀和

1、基本概念

数组 a[0]~a[n-1]，前缀和 sum[i] 等于 a[0]~a[i] 的和：sum[0]=a[0]、sum[1]=a[0] +a[1]、sum[2] = a[0] + a[1] + a[2].......
能在 O(n) 时间内求得所有前缀和：sum[i] = sum[i-1] + a[i]
预计算出前缀和，能快速计算出区间和：a[i] + a[i+1] + ... + a[ j-1 ] + a[ j ] = sum[ j ] - sum[i-1]
复杂度为 O(n) 的区间和计算，优化到了 O(1) 的前缀和计算

2、前缀和与差分的关系

一维差分数组 D[k] = a[k] - a[k-1]，即原数组 a[ ] 的相邻元素的差

差分是前缀和的逆运算：把求 a[k] 转化为求 D 的前缀和

3、差分数组能提升修改的效率

把区间 [L，R] 内每个元素 a[ ] 加上 d，只需要把对应的 D[ ] 做以下操作：

（1）把 D[L] 加上 d：D[L] += d

（2）把 D[R+1] 减去 d：D[R+1] -= d

原来需要 O(n) 次计算，现在只需要 O(1)

前缀和 a[x] = D[1] + D[2] + ... + D[x]，有：

（1）1≤x<L，前缀和 a[x] 不变；

（2） L≤x≤R，前缀和 a[x] 增加了 d；

（3） R<x≤N，前缀和 a[x] 不变，因为被 D[R+1] 中减去的 d 抵消了。

三、例题

1、统计子矩阵（lanqiao2109，2022年省赛）

【题目描述】

有 K 位小朋友到小明家做客。小明拿出了巧克力招待小朋友们。小明一共有 N 块巧克力，其中第 i 块是 Hi×Wi 的方格组成的长方形。为了公平起见，小明需要从这 N 块巧克力中切出 K 块巧克力分给小朋友们。切出的巧克力需要满足：（1）形状是正方形，边长是整数；（2）大小相同。

例如一块 6×5 的巧克力可以切出 6 块 2×2 的巧克力或者 2 块 3×3 的巧克力。小朋友们都希望得到的巧克力尽可能大，你能帮小明计算出最大的边长是多少？

【输入描述】

第一行包含两个整数 N，K (1<=N, K<=10^5)。以下 N 行每行包含两个整数 Hi，Wi (1<=Hi,Wi<=10^5)。输入保证每位小朋友至少能获得一块1×1 的巧克力。

【输出描述】

输出切出的正方形巧克力最大可能的边长。

【问题描述】

给定一个 N×M 的矩阵A，请你统计有多少个子矩阵 (最小 1×1，最大 N×M)，满足子矩阵中所有数的和不超过给定的整数K ？

【输入格式】

第一行包含三个整数 N, M和K，之后 N 行每行包含 M 个整数，代表矩阵 A。

【输出格式】

一个整数代表答案。

【样例输入】

3 4 10

1 2 3 4

5 6 7 8

9 10 11 12

【样例输出】

19

【评测用例规模与约定】

30%的数据，N, M<=20 5分

70%的数据，N, M<=100 10分

100%的数据，1<=N, M<=500 15分

0<=Aij<=1000；1<=K<=250000000

下面一起看看上面三种分数对应的解法！

（1）处理输入

【输入格式】

第一行包含三个整数 N,M 和 K，之后 N 行每行包含 M 个整数，代表矩阵 A。

Python如何读矩阵？定义矩阵 a[][] 从 a[1][1] 读到 a[n][m]

按照下面这样读入可以节省内存，每行的列表开始的时候只有一个元素。

n,m,k=map(int,input().split())

a=[[0] for i in range(n)]
a.insert(0,[0]*(m+1))

for i in range(1,n+1):      #从a[1][1]开始，读矩阵
    a[i].extend(map(int,inpput().split()))

（2）方法一：纯暴力（30%）

【思路】

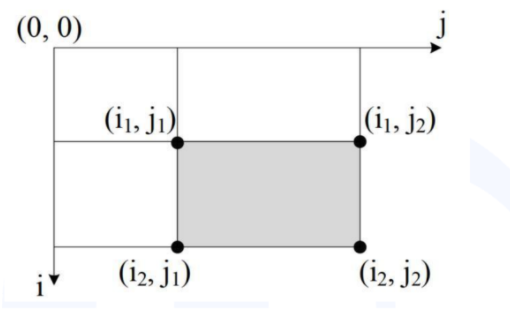
用 i1、i2、j1、j2 框出一个子矩阵

用 i、j 两重 for 循环统计子矩阵和

【复杂度】

6 个 for 循环，O(N^6)

n,m,k=map(int,input().split())

a=[[0] for i in range(n)]
a.insert(0,[0]*(m+1))

for i in range(1,n+1):      #从a[1][1]开始，读矩阵
    a[i].extend(map(int,input().split()))

ans=0
for i1 in range(1,n+1):
    for i2 in range(i1,n+1):
        for j1 in range(1,m+1):
            for j2 in range(j1,m+1):
                summ=0
                for i in range(i1,i2+1):
                    for j in range(j1,j2+1):
                        summ+=a[i][j]
                if summ<=k:
                    ans+=1
print(ans)

（3）方法二：前缀和（70%）

【思路】

“二维前缀和”，定义 s[ ][ ]：s[ i ][ j ] 表示子矩阵 [1, 1]~[i, j] 的和

（1）预计算出 s[ ][ ]，然后快速计算二维子区间和；

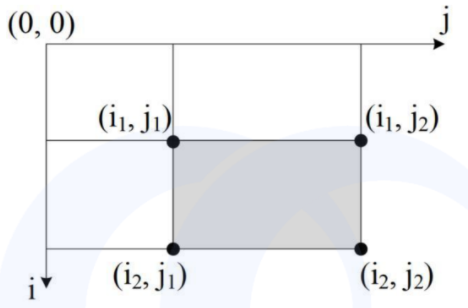
（2）阴影子矩阵 [i1, j1] ~ [i2, j2] 区间和，等于：s [i2][j2] - s[i2][j1-1] - s[i1-1][j2] + s[i1-1][j1-1]

其中 s[i1-1][ j1-1] 被减了 2 次，需要加回来 1 次

【复杂度】

4个for循环，O(N^4)

【预计算前缀和】

“二维前缀和”，定义 s[ ][ ]： s[i][j] 表示子矩阵 [1, 1]~[i, j] 的和

n,m,k=map(int,input().split())

a=[[0] for i in range(n)]
a.insert(0,[0]*(m+1))

for i in range(1,n+1):      #从a[1][1]开始，读矩阵
    a[i].extend(map(int,input().split()))

s=[[0]*(m+1) for i in range(n+1)]   #预计算前缀和s[][]
for i in range(1,n+1):
    for j in range(1,m+1):
        s[i][j]=s[i-1][j]+s[i][j-1]-s[i-1][j-1]+a[i][j]

【计算子矩阵和】

阴影子矩阵 [i1, j1] ~ [i2, j2] 区间和，等于：

s[i2][j2] - s[i2][j1-1] - s[i1-1][j2] + s[i1-1][i1-1]

n,m,k=map(int,input().split())

a=[[0] for i in range(n)]
a.insert(0,[0]*(m+1))

for i in range(1,n+1):      #从a[1][1]开始，读矩阵
    a[i].extend(map(int,input().split()))

s=[[0]*(m+1) for i in range(n+1)]   #预计算前缀和s[][]
for i in range(1,n+1):
    for j in range(1,m+1):
        s[i][j]=s[i-1][j]+s[i][j-1]-s[i-1][j-1]+a[i][j]

ans=0
for i1 in range(1,n+1):
    for i2 in range(i1,n+1):
        for j1 in range(1,m+1):
            for j2 in range(j1,m+1):
                sum=s[i2][j2]-s[i2][j1-1]-s[i1-1][j2]+s[i1-1][j1-1]
                if sum<=k:
                    ans+=1
print(ans)

（4）方法三：前缀和+尺取法（100%）

【思路】

本题统计二维子矩阵和 <=k 的数量，而不用具体指出是哪些子矩阵，可以用尺取法优化。

以一维区间和为例，查询有多少子区间 [j1, j2] 的区间和 s[j2] - s[j1] ≤ k。

暴力法

用 2 重 for 循环遍历 j1 和 j2，复杂度O(n^2)。

尺取法求一维区间和

若 s[j2] - s[j1] <= k，那么在子区间 [j1, j2] 上，有 j2 - j1 + 1 个子区间满足 <= k。用同向扫描的尺取法，用滑动窗口 [j1, j2] 遍历，复杂度降为 O(n)。

尺取法求二维区间和

矩阵的行子区间和仍用 2 重暴力遍历

只把列区间和用尺取法优化

n,m,k=map(int,input().split())
a=[[0] for i in range(n)]
a.insert(0,[0]*(m+1))
for i in range(1,n+1):      #从a[1][1]开始，读矩阵
    a[i].extend(map(int,input().split()))
s=[[0]*(m+1) for i in range(n+1)]   #预计算前缀和s[][]
for i in range(1,n+1):
    for j in range(1,m+1):
        s[i][j]=s[i-1][j]+a[i][j]    #第9行
ans=0
for i1 in range(1,n+1):
    for i2 in range(i1,n+1):
        j1=1;z=0
        for j2 in range(1,m+1):
            z+=s[i2][j2]-s[i1-1][j2]    #第15行
            while z>k:
                z-=s[i2][j1]-s[i1-1][j1]
                j1+=1
            ans+=j2-j1+1
print(ans)

第9行，求第 j 列上，第 1 行到第 i 行上数字的前缀和。

第 11、12 行用 2 重暴力遍历行。

第 14 行：尺取法，滑动窗口 [j1, j2]。移动指针 j2

第15行：第 j2 列上，i1～i2 的区间和。累加得到二维区间和

第16行：若区间和 >k，移动指针 j1

第19行：若 j1~j2 的区间和 <k，那么有 j2-j1+1 个满足

【复杂度】

3 个 for 循环，O(N^3) 刚刚能通过题目的 100% 测试。

（5）个人拙见

Python 组可能不会出这种题，这一题是 C/C++ B组题

Python 的 for 循环极慢，1千万次的循环超过10秒。本题100%的测试运行时间超过10秒。

2、灵能传输（lanqiaoOJ题号196）

题目描述

题目背景

在游戏《星际争霸 II》中，高阶圣堂武士作为星灵的重要 AOE 单位，在游戏的中后期发挥着重要的作用，其技能"灵能风暴"可以消耗大量的灵能对一片区域内的敌军造成毁灭性的伤害。经常用于对抗人类的生化部队和虫族的刺蛇飞龙等低血量单位。

问题描述

你控制着 n 名高阶圣堂武士，方便起见标为 1,2,⋅⋅⋅,n。每名高阶圣堂武士需要一定的灵能来战斗，每个人有一个灵能值 ai 表示其拥有的灵能的多少，ai 非负表示这名高阶圣堂武士比在最佳状态下多余了 ai 点灵能，ai 为负则表示这名高阶圣堂武士还需要 −ai 点灵能才能到达最佳战斗状态）。

输入描述

输出描述

输出 T 行。每行一个整数依次表示每组询问的答案。

输入输出样例

输入：

3

3

5 -2 3

4

0 0 0 0

3

1 2 3

输出：

3

0

3

运行限制

最大运行时间：1s
最大运行内存: 256M

这题和前缀和有关：

（1）所有加减操作都是在数组内部进行，也就是说对于整个数组的和不会有影响;

（2）一次操作是对连续的 3 个数 a[i-1]、a[i]、a[i+1]，根据 a[i-1]+=a[i]，a[i+1]+=a[i]， a[i]=-2a[i]，得前缀和 s[i+1] 的值不变，因为这些数的加减都是在 a[i-1]、a[i]、a[i+1] 内部进行的。另外三个数的和不变。

分析一次操作后的前缀和：

（1）a[i-1] 更新为 a[i]+a[i-1]，那么 s[i-1] 的新值等于原来的 s[i]；

（2）a[i] 更新为 -2a[i]，那么 s[i] 的新值等于原来的 s[i-1]；

（3）a[i+1] 更新为 a[i]+a[i+1]，s[i+1]的值保持不变。

经过一次操作后，s[i] 和 s[i-1] 互相交换，s[i+1] 不变。而 s[i-1]、s[i]、 s[i+1] 这 3 个数值还在，没有出现新的数值。设 a[0]=0，观察前缀和数组 s[0]、 s[1]、 s[2]、 ...、s[n-1]、s[n]。除了 s[0]、s[n] 外，其他的 s[1]、s[2]、…、s[n-1]，经过多次操作后，每个 s[i] 能到达任意位置。

也就是说，题目中对 a[ ] 的多次操作后的一个结果，对应了前缀和 s[ ] 的一种排列。因为 a[i]=s[i]-s[i1]，对 a[ ] 多次操作后的结果是：

a[1] = s[1] - s[0]，a[2] = s[2] - s[1]，...，a[n] = s[n] - s[n-1]

经过以上转换，题目的原意 “对连续 3 个数做加减操作后，求最大的 a[ ] 能达到多小”，变成了比较简单的问题 “数组 s[]，求 max{|s[1]-s[0]|，|s[2]-s[1]|, ..., |s[n]-s[n-1]|}”。

根据题目的要求，s[0] 和 s[n] 保持不动，其他 s[ ] 可以随意变换位置。

先看一个特殊情况，若 s[0] 是最小的， s[n] 是最大的，那么简单了，把 s[ ] 排序后， max{ |s[i]-s[i-1]| ]就是解。

若 s[0] 不是最小的，s[n] 不是最大的，事情比较麻烦。先把 s[ ] 排序，s[0] 和 s[n] 在中间某两个位置，见下图。

此时应该从 s[0] 出发，到最小值 min，然后到最大值 max，最后到达 s[n]，如图所示路线 1->2->3，这样产生的 |s[i]-s[i-1]| 会比较小。

最后一个问题是，图中存在重叠区，[min, s0] 和 [sn, max] 上有重叠。例如在 [min, s0] 上来回走了两遍，但是这区间的每个数只能用一次，解决办法是隔一个数取一个。
还有一个问题，如何处理重叠区？用 vis[i]=1 记录第一次走过的时候第 i 数被取过，第二次再走过时，vis[ ]=1 的数就不用再取了。
本题难在思维，代码好写。

T=int(input())
for t in range(T):
    n=int(input())
    a=list(map(int,input().split()))
    s=[0]+a
    for i in range(1, n+1):
        s[i] += s[i-1]  #前缀和
    s0=0
    sn=s[n]
    if s0>sn:
       sn,s0=s0,sn     #交换:swap(s0, sn)
    s. sort()
    for i in range(n+1):    #找s[0]和s[n]的位置
        if s[i]==s0:
            s0 = i
            break
    for i in range(n,-1,-1):
        if s[i]==sn:
            sn = i;
            break
    L,R=0,n
    a=[0 for i in range(n+1)]
    a[n]=s[n]
    vis=[True for i in range(n+1)]
    for i in range(s0,-1,-2):
        a[L]=s[i];
        L+=1;
        vis[i]=False
    for i in range(sn, n+1,2):
        a[R]=s[i];
        R-=1;
        vis[i]=False
    for i in range(n+1):
        if vis[i]:
            a[L]=s[i]
            L+=1
    res = 0
    for i in range(n):
        res=max(res,abs(a[i+1]-a[i]))
    print (res)

以上，前缀和讲解

祝好