T04BF
👋专栏: 算法|JAVA|MySQL|C语言
🫵 小比特 大梦想

此篇文章与大家分享分治算法关于排序排序的专题
对于快速排序在我个人主页专栏 <排序> 有详细的介绍,此专题对快排进行了优化操作,并介绍了优化后的快排的几种运用
如果有不足的或者错误的请您指出!

1.颜色分类

题目:颜色分类

1.1解析

这道题目实际上就是将一个给定的只有0,1,2的数组,分成三块,0放在一起,1放在一起,2放在一起

回顾一下移动0问题,实则就是利用双指针将数组划分为两部分.本题也可以利用类似的思想,只不过是将数组划分为3部分

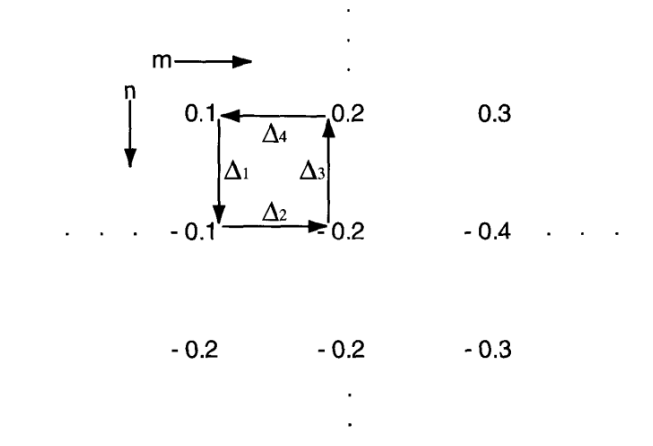
如图所示,我们标记好left和right,用i来遍历数组,那么这三个变量实际上就将数组划分为4个区间,而我们要做的就是在遍历数组的时候去维护三个区间就好了

(1)arr[i] == 0

为了维护0都在[0,left]这段区间,那么我们要让交换arr[++left]和arr[i],后i++继续遍历

(2)arr[i] == 1

为了维护1都在[left+1,i]这段区间,我们只需让i++即可

(3)arr[i] == 2

为了维护2都在[right,n-1(n为数组长度)],我们要让arr[–right]和arr[i]交换,但是此时i不能++,因为此时从[right,n-1]交换过来的元素还没判断

维护好这三个区间,当i与right相遇即可

class Solution {
    public void sortColors(int[] arr) {
        int left = -1;
        int n = arr.length;
        int right = n;
        for(int i = 0; i < right; ){
            if(arr[i] == 0){
                swap(arr,i++,++left);
            }else if(arr[i] == 1){
                i++;
            }else{
                swap(arr,i,--right);
            }
        }
    }
    public void swap(int[] array,int i,int j){
        int tmp = array[i];
        array[i] = array[j];
        array[j] = tmp;
    }
}

2.利用数组划分实现快速排序

题目:数组排序

2.1解析

我们之前学过的快速排序是每次把数组划分为两部分,时间复杂度最好情况下为O(NlogN),但是如果出现大部分的相同元素,就会大大增加时间复杂度

在本题中,我们对之前学过的快速排序进行优化

(1)跟上一题颜色划分一样,在找定基准元素key后,我们把区间每次都分成三部分,

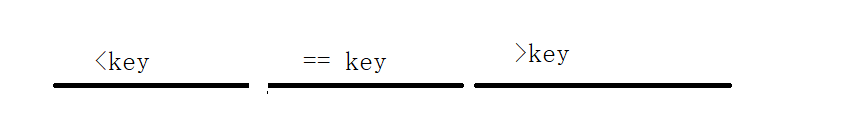
这样做的好处是,我们再次对不同区间进行递归的时候,就不必再考虑中间 == key 的部分了,因为中间都是相同的值,就没必要参与排序了

而分区域的思想在上一道颜色划分的题目已经讲过

实际上就是用i来遍历区间的时候,分三种情况:(推导过程在上一道题已经演示)

①nums[i] < key => swap(i++,++left)

②nums[i] == key => i++

③nums[i] > key => swap(i,–right)

(2)基准元素

我们在之前讲过的快速排序中,基准元素要么是端点值,要么是利用三数取中,但是最优秀的解法应该是等概率的随机在区间里面找基准元素

那么我们就可以利用随机数的方式,即在区间范围内产生随机数下标 random.nextInt(R-L+1)+L

2.2题解

class Solution {
    public int[] sortArray(int[] nums) {
        qsort(nums,0,nums.length-1);
        return nums;
    }
    private void qsort(int[] nums,int l,int r){
        if(l >= r){
            return;
        }
        Random random = new Random();
        int key = nums[random.nextInt(r-l+1)+l];
        int left = l-1;
        int right = r+1;
        int i = l;
        while(i < right){
            if(nums[i] < key){
                swap(nums,i++,++left);
            }else if(nums[i] == key){
                i++;
            }else{
                swap(nums,i,--right);
            }
        }
        qsort(nums,l,left);
        qsort(nums,right,r);
    }

    private void swap(int[] nums,int i,int j){
        int tmp = nums[i];
        nums[i] = nums[j];
        nums[j] = tmp;
    }
}

3.快速选择算法

题目:第k个最大的数

3.1解析

此题实际上是我们快排优化版的运用

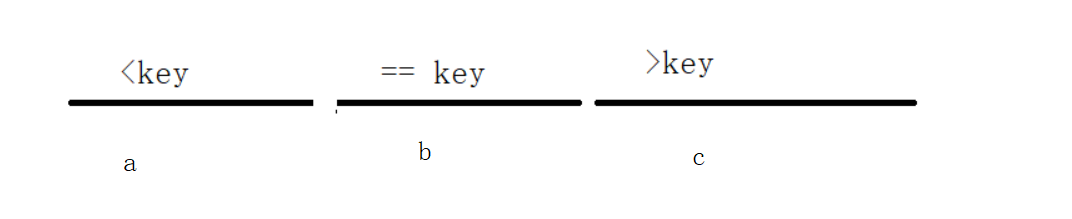
我们在上一题的快速排序中把区间划分为如图所示的三部分,我们分别用a,b,c来表示三部分各自元素个数,那么对于要找的第k个最大元素,就会出现三种情况

(1) c >= k

说明第k个最大元素就是 在c区间的第k个最大元素,那么我们就直接针对c区间进行递归即可,a,b区间不用管

(2)在c >= k 不成立的前提下,如果b + c >= k,那么说明第k个最大元素一定在b区间,而b区间全部都是相同元素,那么直接返回key即可

(2)在前面两个条件都不成立的情况下,那么第k个最大元素只能在a区间,那么我们就要去a区间递归,但是此时就不是找第k个最大元素了

此时由于大元素都在后面,而我们仅仅只是针对a区间寻找,前k个最大元素有b+c个是在b ,c区间里面的,因此我们要在a中寻找的是第k-b-c大的元素

3.2题解

class Solution {
    public int findKthLargest(int[] nums, int k) {
        return qSort(nums,k,0,nums.length-1);
    }
    private int qSort(int[] nums,int k, int l,int r){
        //此时由于下面已经分类讨论了,因此不可能出现无意义区间的情况
        int key = nums[new Random().nextInt(r-l+1)+l];
        int left = l-1;
        int right = r+1;
        int i = l;
        while(i < right){
            if(nums[i] < key){
                swap(nums,i++,++left);
            }else if(nums[i] == key){
                i++;
            }else{
                swap(nums,i,--right);
            }
        } 
        //三个区间为[l,left] [left+1,right-1] [right,r]
        int b = right - left - 1;
        int c = r - right + 1;
        if(c >= k){
            return qSort(nums,k,right,r);
        }else if(b + c >= k){
            return key;
        }else{
            return qSort(nums,k-b-c,l,left);
        }
    }

    private void swap(int[] nums,int i,int j){
        int tmp = nums[i];
        nums[i] = nums[j];
        nums[j] = tmp;
    }
}

4.最小的k个数

题目:最小的k个数

4.1解析

我们一开始想到的方法可能就是直接排序,然后返回前k个最小的数

但是题目对于返回的数组里面的元素是否有序并不关心

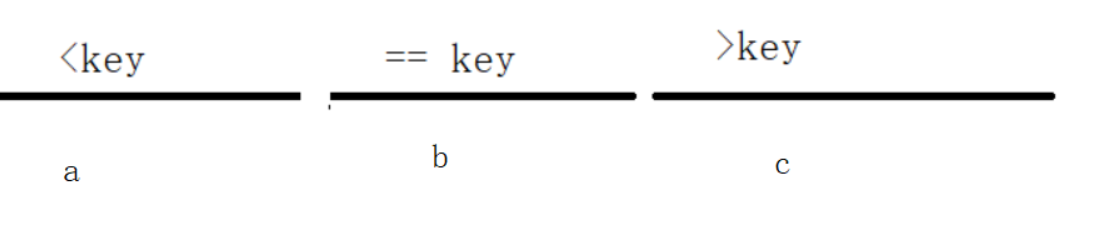
我们在上面的快排中将区间分成三部分,那么对于最小的前k个元素,也会出现三种情况

(1)a > k,那么最小的前k个元素就都在a区间,我们直接去a区间递归即可

(2)在a > k不成立的前提下,如果a + b >= k,那么说明此时最小的前k个元素分成两部分,一部分在a区间,一部分在b区间,由于不关心返回数组里面元素是否有序,那么我们直接返回此时数组的前k个元素即可

(3)在前面两种情况都不满足的前提下,说明此时最小的前k个元素,一部分是a+b的所有元素,一部分是c里面的元素,那么我们就要去c里面递归寻找第k-a-b个元素

4.2题解

class Solution {
    public int[] inventoryManagement(int[] stock, int cnt) {
        qSort(stock,cnt,0,stock.length-1);
        int[] ret = new int[cnt];
        for(int i = 0; i < cnt; i++){
            ret[i] = stock[i];
        }
        return ret;
    }

    private void qSort(int[] stock,int cnt,int l,int r){
        int key = stock[new Random().nextInt(r-l+1)+l];
        int left = l-1;
        int right = r+1;
        int i = l;
        while(i < right){
            if(stock[i] < key){
                swap(stock,i++,++left);
            }else if(stock[i] == key){
                i++;
            }else{
                swap(stock,i,--right);
            }
        }
        //[l,left] [left+1,right-1] [right,r]
        int a = left - l + 1;
        int b = right - left - 1;
        if(a > cnt){
            qSort(stock,cnt,l,left);
        }else if(a + b >= cnt){
            return;
        }else{
            qSort(stock,cnt-a-b,right,r);
        }
    }

    private void swap(int[] nums,int i,int j){
        int tmp = nums[i];
        nums[i] = nums[j];
        nums[j] = tmp;
    }
}

​

感谢您的访问!!期待您的关注!!!

T04BF
🫵 小比特 大梦想