React之Diff 算法

在 React 中，通过 React.createElement 也能生成一个虚拟 DOM 节点（ReactElement）。在 React15 及以前，采用了递归的方式创建虚拟 DOM，递归过程是不能中断的。如果组件树的层级很深，递归会占用线程很多时间，造成卡顿。React16 将递归的无法中断的更新重构为异步的可中断更新，推出了新的 Fiber 架构。

原本的 ReactElement 只有 children，在中断恢复时，无法找到其兄弟节点和父节点，无法从断点处继续完成渲染工作。而 fiber 节点上能访问到父节点、子节点、兄弟节点，所以即使渲染被打断了，也可以恢复查找未处理的节点。因此，React 需要先生成 ReactElement，再生成 fiber，最后才将变更映射到真实 DOM 节点。Vue 与 React 不同，它通过递归的形式生成整个虚拟 DOM 树，在 diff 的同时会对 DOM 做变更。

React 采用了双缓存的技术，在 React 中最多会存在两颗 fiber 树，当前屏幕上显示内容对应的 fiber 树称为 current fiber 树，正在内存中构建的 fiber 树称为 workInProgress fiber 树。当 workInProgress fiber 树构建并渲染到页面上后，应用根节点的 current 指针指向 workInProgress Fiber 树，此时 workInProgress Fiber 树就变为 current Fiber 树。

React 的更新会经历两个阶段：render 阶段和 commit 阶段。render 阶段是可中断的，commit 阶段是不可中断的。

render 阶段会生成 fiber 树，所谓的 diff 就会发生在这个阶段。React 通过深度优先遍历来生成 fiber 树，整个过程与递归是类似的，因此生成 fiber 树的过程又可以分为「递」阶段和「归」阶段。
commit 阶段主要执行各种 DOM 操作、生命周期钩子、某些 hook 等。

因此，diff 阶段不会直接变更 DOM，而是留到 commit 阶段再做变更。

React 如何知道哪些 DOM 节点需要被更新呢？

在render阶段的beginWork函数中，会将上次更新产生的 Fiber 节点与本次更新的 JSX 对象（对应ClassComponent的this.render方法返回值，或者FunctionComponent执行的返回值）进行比较。根据比较的结果生成workInProgress Fiber，即本次更新的 Fiber 节点。即，React 将上次更新的结果与本次更新的值比较，只将变化的部分体现在 DOM 上。这个比较的过程，就是 Diff。

由于 Diff 操作本身也会带来性能损耗，React文档中提到，即使在最前沿的算法中，将前后两棵树完全比对的算法的复杂程度为 O(n^3 )，其中 n 是树中元素的数量。

O(n³) 由来

关于 O(n³) 的由来。由于左树中任意节点都可能出现在右树，所以必须在对左树深度遍历的同时，对右树进行深度遍历，找到每个节点的对应关系，这里的时间复杂度是 O(n²)，之后需要对树的各节点进行增删移的操作，这个过程简单可以理解为加了一层遍历循环，因此再乘一个 n。

为了降低算法复杂度，React 的 diff 会预设三个限制：

Tree Diff（树策略）: 只对同级元素进行Diff。如果一个DOM节点在前后两次更新中跨越了层级，那么 React 不会尝试复用他。因为，Web UI 中 DOM 节点跨层级的移动操作特别少，可以忽略不计。
Component Diff（组件策略）: 拥有相同类的两个组件将会生成相似的树形结构，拥有不同类的两个组件将会生成不同的树形结构
Element Diff（元素策略）：对于同一层级的一组子节点，它们可以通过唯一 id 进行区分。开发者可以通过 key 属性来暗示哪些子元素在不同的渲染下能保持稳定。

React 进行 tree diff、component diff 和 element diff进行算法优化是基于上面三个前提策略。事实证明上面的三个前提策略是非常有效的。

Diff 入口

function reconcileChildFibers(
    returnFiber: Fiber,
    currentFirstChild: Fiber | null,
    newChild: any,
    lanes: Lanes,
  ): Fiber | null {
    // ...

    // 判断 newChild 类型
    const isObject = typeof newChild === 'object' && newChild !== null;

    // object类型，可能是 REACT_ELEMENT_TYPE 或 REACT_PORTAL_TYPE 等  
    if (isObject) {
      switch (newChild.$$typeof) {
        case REACT_ELEMENT_TYPE:
          // 调用 reconcileSingleElement 处理
          return placeSingleChild(
            reconcileSingleElement(
              returnFiber,
              currentFirstChild,
              newChild,
              lanes,
            ),
          );
        case REACT_PORTAL_TYPE:
          // 调用 reconcileSinglePortal 处理    
          // ....
        case REACT_LAZY_TYPE:
          // 调用 reconcileChildFibers 处理    
          // ....
      }
    }

    // newChild 是字符串或数字 调用 reconcileSingleTextNode 处理   
    if (typeof newChild === 'string' || typeof newChild === 'number') {
      return placeSingleChild(
        reconcileSingleTextNode(
          returnFiber,
          currentFirstChild,
          '' + newChild,
          lanes,
        ),
      );
    }

    // newChild 是数组 调用 reconcileChildrenArray 处理
    if (isArray(newChild)) {
      return reconcileChildrenArray(
        returnFiber,
        currentFirstChild,
        newChild,
        lanes,
      );
    }
 // newChild 迭代器 reconcileChildrenIterator 处理
    if (getIteratorFn(newChild)) {
      return reconcileChildrenIterator(
        returnFiber,
        currentFirstChild,
        newChild,
        lanes,
      );
    }
    // ....    

    // 以上都没有命中，删除节点
    return deleteRemainingChildren(returnFiber, currentFirstChild);
 }

可以从同级的节点数量将 Diff 分为两类：

单节点条件：当newChild类型为object、number、string，代表同级只有一个节点
多节点条件：当newChild类型为Array，同级有多个节点

单节点 Diff

对于单个节点，当newChild类型为object、number、string，代表同级只有一个节点，会进入reconcileSingleElement

function reconcileSingleElement(
    returnFiber: Fiber,
    currentFirstChild: Fiber | null,
    element: ReactElement,
    lanes: Lanes,
  ): Fiber {
    const key = element.key;
    let child = currentFirstChild;
        
    // 首先判断是否存在对应 DOM 节点
    while (child !== null) {
      // 上一次更新存在 DOM 节点，接下来判断是否可复用
      // 首先比较 key 是否相同  
      if (child.key === key) {
        // key 相同，接下来比较 type 是否相同
        switch (child.tag) {
          case Fragment: // ...
          case Block: // ...
          default: {
            if (child.elementType === element.type ) {
              // 情况一：key 和 type 都相同则表示可以复用 返回复用的 fiber
              return existing;
            }
            // type 不同则跳出 switch
            break;
          }
        }
        // Didn't match.
        // 情况二：key 相同但是 type 不同 将该 fiber 及其兄弟 fiber 标记为删除
        deleteRemainingChildren(returnFiber, child);
        break;
      } else {
        // 情况三：key 不同，Type也不同，将该 fiber 标记为删除
        deleteChild(returnFiber, child);
      }
      child = child.sibling;
    }
 // 创建新 fiber
    if (element.type === REACT_FRAGMENT_TYPE) {
      const created = createFiberFromFragment(
        element.props.children,
        returnFiber.mode,
        lanes,
        element.key,
      );
      created.return = returnFiber;
      return created;
    } else {
      const created = createFiberFromElement(element, returnFiber.mode, lanes);
      created.ref = coerceRef(returnFiber, currentFirstChild, element);
      created.return = returnFiber;
      return created;
    }
  }

React 通过先判断 key 是否相同，如果 key 相同则判断 type 是否相同，只有都相同时一个 DOM节点 才能复用。

当child !== null且key相同且type不同时执行deleteRemainingChildren将child及其兄弟fiber都标记删除。
当child !== null且key不同时仅将child标记删除。

小结

单节点条件：newChild 类型为 object、number、string，代表同级只有一个节点。
单节点复用条件：key 和 type 都相等，否则不可复用节点。
- key 相同：child.key === key。没有设置 key 则为 null。新旧节点 key 都为 null，也认为 key 相同。
- type 相同：child.elementType === element.type
单节点 diff 规则：child 存在的情况下（有节点），先判断 key 是否相同，如果 key 相同则判断 type 是否相同，只有都相同时一个 DOM节点 才能复用。
- key 相同 & type 相同：可以复用返回复用的 fiber
- key 相同 & type 不同：将该 fiber 及其兄弟 fiber 标记为删除
- key 不同：将该 fiber 标记为删除
没有节点，则直接新建

多节点 Diff

React 每次更新时，会将新的 ReactElement（即 React.createElement() 的返回值）与旧的 fiber 树作对比，比较出它们的差异后，构建出新的 fiber 树，因此多节点的 diff 实际上是用 fiber（旧子节点）和 ReactElement 数组（新子节点）进行对比。多节点 DIff 无非以下情况：

节点更新（属性、类型）
节点新增或删除
节点位置变化

在日常开发中，相较于新增和删除，更新组件发生的频率更高。所以Diff会优先判断当前节点是否属于更新。

多节点 Diff算法的整体逻辑会经历两轮遍历：

第一轮遍历：处理更新的节点。
第二轮遍历：处理剩下的不属于更新的节点。

function reconcileChildrenArray(
    returnFiber: Fiber,
    currentFirstChild: Fiber | null,
    newChildren: Array<*>, // 新节点
    lanes: Lanes,
  ): Fiber | null {
    // 列表中使用 React element 数据更新了属性的第一个 Fiber 节点
    let resultingFirstChild: Fiber | null = null;
    // 上一个更新了属性的 Fiber 节点，用以列表中兄弟节点的相互关联
    let previousNewFiber: Fiber | null = null; 
    // current 树上的列表中的第一个Fiber节点
    let oldFiber = currentFirstChild; 
    // 上一个元素移动位置的下标    
    let lastPlacedIndex = 0; 
    // 遍历 React element 树的下标    
    let newIdx = 0; 
    // current 树上的列表中元素的兄弟节点    
    let nextOldFiber = null; 
        
    // 第一轮遍历：这个 for 循环的作用是剔除没有变化的节点，并对节点进行更新和重用
    // 当检查到尾部有新增节点时，oldFiber 为 null，则会跳出循环，
    // 然后创建新的 Fiber 插入到尾部，不需要与其它节点进行对比
    // 当有新节点想在中间插入，newFiber 则为 null，则会跳出循环，然后需要移动节点位置进行排序
    for (; oldFiber !== null && newIdx < newChildren.length; newIdx++) {
      if (oldFiber.index > newIdx) {
        nextOldFiber = oldFiber;
        oldFiber = null;
      } else {
        nextOldFiber = oldFiber.sibling;
      }
      // 判断旧 Fiber 节点上的 key 与 React element 上的 key 属性是否相等
      // key 相等，则会使用 React element 的数据更新 Fiber 节点上的属性
      // key 不相等，则会返回 null
      const newFiber = updateSlot(
        returnFiber,
        oldFiber,
        newChildren[newIdx], // 遍历 newChildren
        lanes,
      );
      // 发现有元素的 key 属性有变化，说明不是更新场景，则会跳出 for 循环
      if (newFiber === null) {
        if (oldFiber === null) {
          oldFiber = nextOldFiber;
        }
        break;
      }
      if (shouldTrackSideEffects) {
        if (oldFiber && newFiber.alternate === null) {
          deleteChild(returnFiber, oldFiber);
        }
      }
      // 将 newIdx 赋值给 workInProgress 树上的 Fiber 节点的 index 属性，代表当前元素在列表中的位置（下标）
      // 判断 current 树上元素的 Index 是否小于 lastPlacedIndex，是则表示该元素需要移动位置，否则表示不需要移动位置
      lastPlacedIndex = placeChild(newFiber, lastPlacedIndex, newIdx);
      if (previousNewFiber === null) {
        resultingFirstChild = newFiber;
      } else {
        // 将更新了属性的兄弟 Fiber 节点进行关联
        previousNewFiber.sibling = newFiber;
      }
      previousNewFiber = newFiber;
      oldFiber = nextOldFiber;
    }
    // 新的子节点已经遍历完成，如果还有剩下的节点，表示 current 树上有，
    // 但是 workInProgress 树上没有的节点，需要全部删除
    if (newIdx === newChildren.length) {
      deleteRemainingChildren(returnFiber, oldFiber);
      return resultingFirstChild;
    }
    // 节点新增，不需要与旧节点对比，直接创建新增
    if (oldFiber === null) {
      for (; newIdx < newChildren.length; newIdx++) {
        const newFiber = createChild(returnFiber, newChildren[newIdx], lanes);
        if (newFiber === null) {
          continue;
        }
        lastPlacedIndex = placeChild(newFiber, lastPlacedIndex, newIdx);
        if (previousNewFiber === null) {
          resultingFirstChild = newFiber;
        } else {
          previousNewFiber.sibling = newFiber;
        }
        previousNewFiber = newFiber;
      }
      return resultingFirstChild;
    }

    // 将 current 树上的列表中还未对比的元素添加进 Map 对象中
    // 下面的 for 循环会根据 key 取出 Map 中对应的旧的 Fiber 与 React element 做类型的比较
    // 如果类型相同则更新 Fiber 属性，不同，则会根据 React element 重新创建一个新的 Fiber 做插入操作
    const existingChildren = mapRemainingChildren(returnFiber, oldFiber);

    // 节点移动
    for (; newIdx < newChildren.length; newIdx++) {
      // 根据 key 取出 Map 中对应的旧的 Fiber 与 React element 做类型的比较
      // 如果类型相同则使用 React element 的数据更新 Fiber 节点上的属性进行重用
      // 不同，则会根据 React element 的数据重新创建一个新的 Fiber 做插入操作 
      const newFiber = updateFromMap(
        existingChildren,
        returnFiber,
        newIdx,
        newChildren[newIdx],
        lanes,
      );
      if (newFiber !== null) {
        
        if (shouldTrackSideEffects) {
          // newFiber.alternate 不为 null，表示是重用的节点，需要将 existingChildren 中重用的节点删除掉
          // 遍历结束后 existingChildren 中剩下的节点，则是需要删除的    
          if (newFiber.alternate !== null) {
            // 在调用 updateFromMap 方法时，会根据 key 取出相对应的 Fiber
            // 调用 updateFromMap 方法完成后，对应 key 的 Fiber 值被重用了，所以需要删除 Map 中使用过的 key 对应的值  
            existingChildren.delete(
              newFiber.key === null ? newIdx : newFiber.key,
            );
          }
        }
        // 将 newIdx 赋值给 workInProgress 树上的 Fiber 节点的 index 属性，代表当前元素在列表中的位置（下标）
        // 判断 current 树上元素的 Index 是否小于 lastPlacedIndex，是则表示该元素需要移动位置，否则表示不需要移动位置。  
        lastPlacedIndex = placeChild(newFiber, lastPlacedIndex, newIdx);
        if (previousNewFiber === null) {
          resultingFirstChild = newFiber;
        } else {
          previousNewFiber.sibling = newFiber;
        }
        previousNewFiber = newFiber;
      }
    }
    // 节点删除
    if (shouldTrackSideEffects) {
      // existingChildren 中剩下的 Fiber，表示 current 树上存在，但是 workInProgress 树上不存在的元素
      // 将剩下的 Fiber 添加到父 Fiber 节点的 deletions 属性中, 
      // 并且在 flags 集合中添加删除标识，在 commit 阶段会将这些元素进行删除
      existingChildren.forEach(child => deleteChild(returnFiber, child));
    }
    // 返回列表中的第一个节点
    return resultingFirstChild;
  }

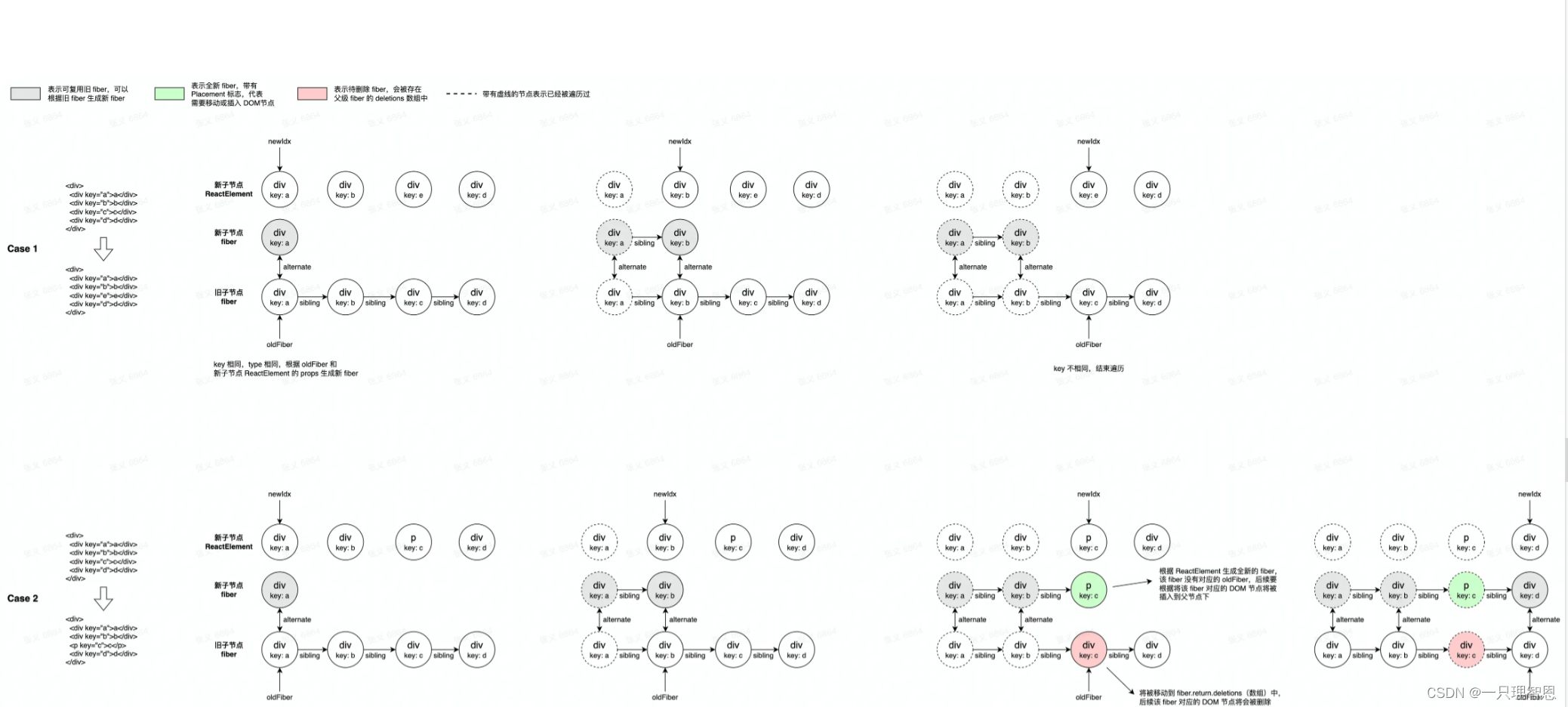
第一轮遍历

从前到后遍历新旧子节点

key 和 type 都相同，则根据旧 fiber 和新 ReactElement 的 props 生成新子节点 fiber。即，使用 React element 的数据更新 Fiber 节点上的属性。 复用旧节点，只更新其属性 props（当然也包含 children）
key 相同，但 type 不同，将根据新 ReactElement 生成新 fiber，旧 fiber 将被添加到它的父级 fiber 的 deletions 数组中，后续将被移除。创建新节点，删除旧节点。
key 不同，结束遍历。

第二轮遍历

如果第一轮遍历被提前终止了，意味着还有新 ReactElement 或 旧 fiber 还未被遍历。因此会有第二轮遍历去处理以下三种情况：

只剩旧子节点
- 说明多余的 oldFiber 在这次更新中已经不存在了，所以需要遍历剩下的 oldFiber，依次执行删除操作（Fiber.effectTag = Deletion）
只剩新子节点
- 说明老的 DOM 节点都复用了，这时还有新加入的节点，意味着本次更新有新节点插入，我们只需要遍历剩下的 newChildren 依次执行插入操作（Fiber.effectTag = Placement）
新旧子节点都有剩
- 说明有节点在这次更新中改变了位置，需要移动节点。由于有节点交换了位置，所以不能再用位置索引对比前后的节点，那么怎样才能将同一个节点在两次更新中对应上呢？这时候就需要用 key 属性了。为了快速的找到 key 对应的 oldFiber，将所有还没处理的 oldFiber 放进以 key 属性为 key，以 Fiber 为 value 的 map，空间换时间。

只剩旧子节点

只剩下旧子节点的处理方法很简单，只需要将剩余的旧 fiber 放到父 fiber 的 deletions 数组中，这些旧 fiber 对应的 DOM 节点将会在 commit 阶段被移除。

只剩新子节点

对于剩余的新子节点，先创建新的 fiber 节点，然后打上 Placement 标记，我们将在遍历 fiber 树的「归」阶段生成这些新 fiber 对应的 DOM 节点。

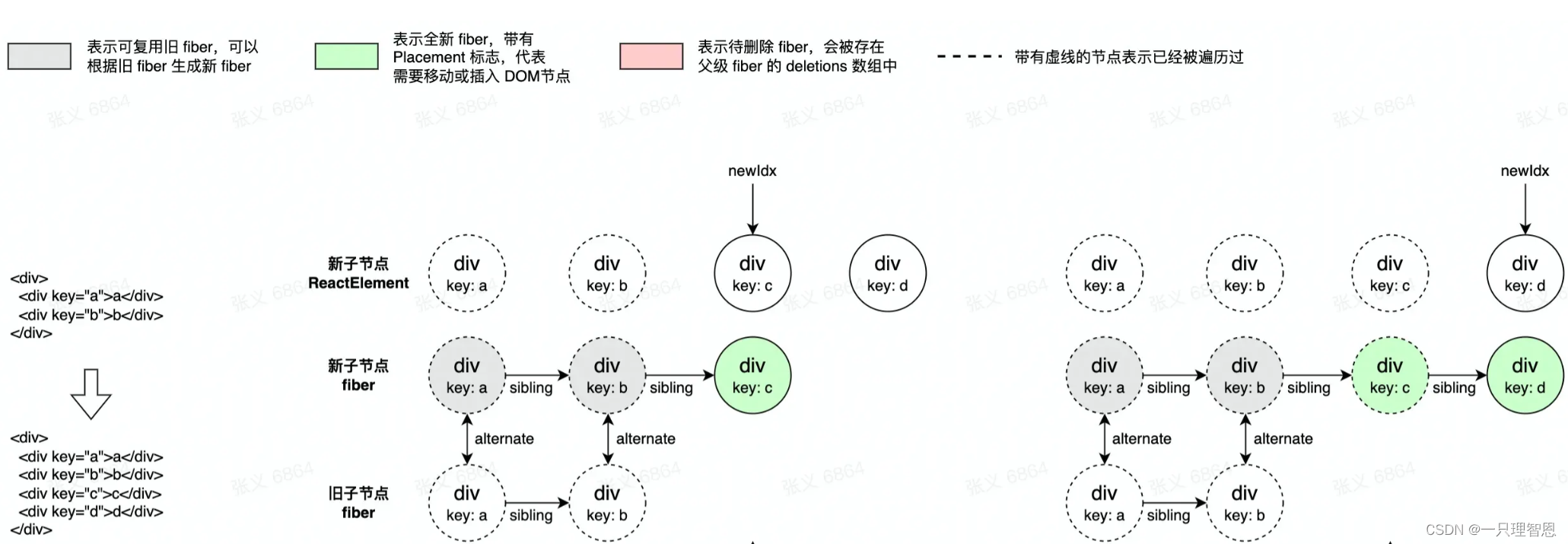
新旧子节点都有剩

由于有节点交换了位置，所以不能再用位置索引对比前后的节点，那么怎样才能将同一个节点在两次更新中对应上呢？这时候就需要用 key 属性了。为了快速的找到 key 对应的 oldFiber，将所有还没处理的 oldFiber 放进以 key 属性为 key，以 Fiber 为 value 的 map，空间换时间。

这种情况下，需要一个快速的方法帮助我们快速找到某个 ReactElement 在上一次渲染时生成的 fiber 节点。因此，我们需要一个 existingChildren Map，这个 Map 保存了旧 fiber 的 key 到旧 fiber 的映射关系，我们可以通过新的 ReactElement 的 key 快速在这个 Map 中找到对应的旧 fiber：

能找到，则能复用旧 fiber 以生成新 fiber
找不到，证明要生成新的 fiber，并打上一个 Placement 标志，以便于在 commit 阶段插入该 fiber 对应的 DOM 节点。

我们还需要找到哪些节点的位置发生了变化。

假设我们有 a、b、c、d 四个节点，它们的位置索引是 0、1、2、3，是一个递增的序列。在更新后，它们顺序发生了变化，变成了 a、c、b、d，那么它们的位置索引变为 0、2、1、3（继续沿用旧的位置索引），不再是一个递增的序列，因为索引 1 移到了 2 的后面（即 b 原本在 c 前面，更新后被移到了 c 后面），破坏了递增的规律。因此，只需要找到那些破坏了索引递增规律的节点，就知道哪些节点的位置发生了变化。那具体要怎么做呢？

其实，旧 fiber 上有 index 属性，index 属性记录了在上一次渲染时该 fiber 所在的位置索引。

oldIndex：当前可复用节点在旧节点上的位置索引
lastPlacedIndex：把遍历新子节点过程中访问过的最大 oldIndex。该变量表示当前最后一个可复用节点，对应的 oldFiber 在上一次更新中所在的位置索引。我们通过这个变量判断节点是否需要移动。

如果 oldIndex >= lastPlacedIndex 代表该可复用节点不需要移动，并将 lastPlacedIndex = oldIndex; 如果 oldIndex < lastplacedIndex 该可复用节点之前插入的位置索引小于这次更新需要插入的位置索引，代表该节点需要向右移动。那么，只要当前新子节点有对应的旧 fiber，且 oldIndex < lastPlacedIndex，就可以认为该新子节点对应的 DOM 节点需要往后移动，并打上一个 Placement 标志，以便于在 commit 阶段识别出这个需要移动 DOM 节点的 fiber。

遍历流程

遍历未处理的旧子节点，生成 existingChildren Map
从前到后遍历新子节点
- 如果能在 existingChildren Map 中找到对应的旧 fiber，根据旧 fiber 生成新 fiber；如果不能，生成新 fiber，并打上 Placement 标志
- 从 existingChildren Map 中删除已处理的节点
- 如果新子节点有对应的旧 fiber
  - 当 oldIndex < lastPlacedIndex 时，给新 fiber 打上 Placement 标志；否则，令 lastPlacedIndex = newIndex
- 如果新子节点没有对应的旧 fiber，创建一个新 fiber 并打上 Placement 标志
遍历 existingChildren Map，将 Map 中所有节点添加到父节点的 deletions 数组中

Commit 阶段变更

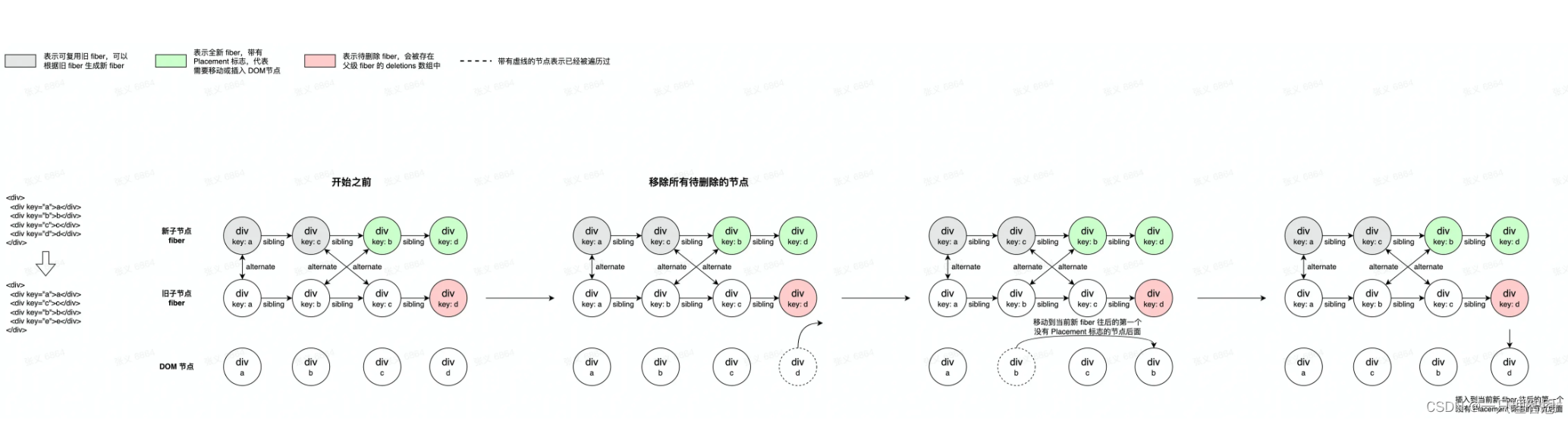
DOM 元素类型的 fiber 节点上存有对 DOM 节点的引用，因此在 commit 阶段，深度优先遍历每个新 fiber 节点，对 fiber 节点对应的 DOM 节点做以下变更：

删除 deletions 数组中 fiber 对应的 DOM 节点
如有 Placement 标志，将节点移动到往后第一个没有 Placement 标记的 fiber 的 DOM 节点之前。
更新节点。以 DOM 节点为例，在生成 fiber 树的「归」阶段，会找出属性的变更集，在 commit 阶段更新属性。

性能缺陷

React 采用仅右移方案，在大部分从左往右移的业务场景中，得到了较好的性能。但在处理节点左移(前移)，表现就不太乐观。

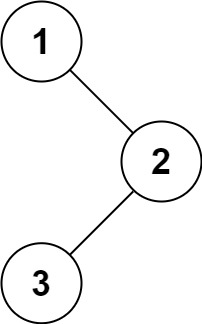
以下图为例，节点 a、b、c、d 变为了d、a、b、c，如果我们手动处理这种位置变化，只需要一步：将 d 节点移动到 a 前面。但 React 实际上的做法有三步：将 a、b、c 三个节点依次插入到 d 节点后面。

这是因为遍历完 d 节点后，lastPlacedIndex 变成了 3，再去遍历 a、b、c、d 时，**oldIndex 一定小于 lastPlacedIndex**了。

因此，实际编写代码时，应该尽量避免节点往前移动的操作。

为什么不用双端 Diff

既然 React 对节点往前移动的情况处理得不好，是不是可以在每次遍历的时候，都尝试和旧子节点中最后一个未处理节点做对比，看看能不能匹配上。实际上，Vue2 的 diff 就是这么做的。

Vue 2 的双端 diff 是旧的一组 VNode（旧子节点）和新的一组 VNode（新子节点）进行对比

所谓的「双端」，表示在新旧子节点的数组中，各用两个指针指向头尾节点，在遍历过程中，头尾指针不断靠拢。因此，用 newStartIndex 和 newEndIndex 分别指向新子节点中未处理节点的头尾节点，用 oldStartIndex 和 oldEndIndex 分别指向旧子节点中未处理节点的头尾节点。

现在，我们用「新前」表示新子节点中未处理节点的第一个节点；用「新后」表示新子节点中未处理节点的最后一个节点；「旧前」表示旧子节点中未处理节点的第一个节点；用「旧后」表示旧子节点中未处理节点的最后一个节点。

每遍历到一个节点，就尝试进行双端比较：「新前 vs 旧前」、「新后 vs 旧后」、「新后 vs 旧前」、「新前 vs 旧后」，如果匹配成功，更新双端的指针。比如，新旧子节点通过「新前 vs 旧后」匹配成功，那么 newStartIndex += 1，oldEndIndex -= 1。

如果新旧子节点通过「新后 vs 旧前」匹配成功，还需要将「旧前」对应的 DOM 节点插入到「旧后」对应的 DOM 节点之前。如果新旧子节点通过「新前 vs 旧后」匹配成功，还需要将「旧后」对应的 DOM 节点插入到「旧前」对应的 DOM 节点之前。

如果通过双端比较都没法找到匹配的节点，就需要一个像 React existingChildren Map 的 Map 对象了，在 Vue2 的 diff 中，这个 Map 名字叫做 oldKeyToIdx Map。通过这个 Map，遍历时就可以尝试根据新子节点的 key 去找 oldIndex，查找结果会有两种：

找到 oldIndex，即新旧子节点中有相同 key 的节点。
- 如果 VNode 的 type 是相同的，将旧子节点对应的 DOM 节点插入到「旧前」对应的 DOM 节点之前。
- 如果 VNode 的 type 是不同的，创建一个新的 DOM 节点，并插入到「旧前」对应的 DOM 节点之前。
没找 oldIndex，需要根据新子节点（VNode）创建 DOM 元素，并插入到「旧前」对应的 DOM 节点之前。

简单来说，第一轮遍历会先尝试比较新旧子节点的双端节点，如果匹配不成功，再尝试在旧子节中找到对应的节点。至于 DOM 节点的移动，需要记住只能移动到「旧前」之前或「旧后」之后。如果更新后节点位置被调到前面了，移动时就需要移到「旧前」之前；如果更新后节点位置被调到后面了，移动时就需要移到「旧后」之后。

如果第一轮遍历后，只剩下新子节点（oldStartIndex > oldEndIndex），则根据剩余的新子节点（VNode）创建 DOM 节点，并依次插入到父级 DOM 节点最后。
如果第一轮遍历后，只剩下旧子节点（newStartIndex > newEndIndex），则将剩余旧子节点对应的 DOM 节点依次从父级 DOM 节点中删除。

需要注意的是，Vue 在 diff 的过程中，会直接进行节点的更新/新建/删除操作，这点和 React 是不同的。

React 在源码注释中解释了为什么不使用双端 diff：

由于双端 diff 需要向前查找节点，但每个 fiber 节点上都没有反向指针，即前一个 fiber 通过 sibling 属性指向后一个 fiber，只能从前往后遍历，而不能反过来（你可以在上文的各个示例图中看到这种实现），因此该算法无法通过双端搜索来进行优化。React 想看下现在用这种方式能走多远，如果这种方式不理想，以后再考虑实现双端 diff。React 认为对于列表反转和需要进行双端搜索的场景是少见的。单链表无法使用双指针，所以无法对算法使用双指针优化。