题目链接

题目描述

给定一个排序数组和一个目标值，在数组中找到目标值，并返回其索引。如果目标值不存在于数组中，返回它将会被按顺序插入的位置。

请必须使用时间复杂度为 O(log n) 的算法。

示例 1:

输入: nums = [1,3,5,6], target = 5
输出: 2

示例 2:

输入: nums = [1,3,5,6], target = 2
输出: 1

示例 3:

输入: nums = [1,3,5,6], target = 7
输出: 4

提示:

• 1 <= nums.length <= 104
• -104 <= nums[i] <= 104
• nums 为 无重复元素 的 升序 排列数组
• -104 <= target <= 104

分析思路

• 前提：有序数组＋数组中无重复元素（一旦有重复元素，使用二分查找法返回的元素下标可能不是唯一的）
• 确认方法：二分查找法
• 注：二分法中关于区间的定义一般为两种——“左闭右闭[left, right]” 或 “左闭右开[left, right)”

代码实现

实现一：左闭右闭

class Solution {
public:
    int searchInsert(vector<int>& nums, int target) {
        int left = 0;
        int right = nums.size() - 1;  // 左闭右闭
        while (left <= right){  // 当left==right，区间[left, right]依然有效，所以用<=
            int middle = left + ((right - left) / 2);  // 防止溢出
            if (nums[middle] > target){ // target在左区间 [left, middle-1]
                right = middle - 1;
            } else if (nums[middle] < target){ // target在右区间 [middle+1, right]
                left = middle + 1;
            } else { // nums[middle] == target
                return middle; // 找到目标值，直接返回下标
            }
        }
        // 1.目标值在数组所有元素之前 [0, -1]
        // 2.目标值插入数组中的位置 [left, right]
        // 3.目标值在数组所有元素之后 [nums.size(), nums.size()-1]
        return right + 1;
        // return left;
    }
};

实现二：左闭右开

class Solution {
public:
    int searchInsert(vector<int>& nums, int target) {
        int left = 0;
        int right = nums.size();  // 左闭右开
        while (left < right){  // 当left==right，区间[left, right)无效
            int middle = left + ((right - left) / 2);  // 防止溢出
            // int middle = left + ((right - left) >> 1); // >>按位右移运算符，等同于变量除以2
            if (nums[middle] > target){ // target在左区间 [left, middle)
                right = middle;
            } else if (nums[middle] < target){ // target在右区间 [middle+1, right)
                left = middle + 1;
            } else { // nums[middle] == target
                return middle; // 找到目标值，直接返回下标
            }
        }
        // 1.目标值在数组所有元素之前 [0, 0)
        // 2.目标值插入数组中的位置 [left, right)
        // 3.目标值在数组所有元素之后 [nums.size(), nums.size() )
        return right;
        // return left;
    }
};

参考来源：代码随想录 

补充：位移运算符为何能将数据乘以或除以  ?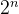

按位右移运算符（>>）将变量除以；按位左移运算符（<<）将变量乘以。

例如：

变量num的值为16，其二进制表示为10000。将num右移1位，结果为01000，即8，这相当于将其减半；将num右移两位，变成了00100，即4，相当于计算num的1/4。向左移1位时结果为100000，即32，向左移两位的结果为1000000，即64，相当于计算num的2倍和4倍。