对于离散时间傅里叶变换(DTFT)及其反变换的讲解,教材里通常会先给出DTFT正变换的公式,再举个DTFT的简单变换例子,推导一下DTFT的性质,然后给出DTFT反变换的公式,再证明一下正变换和反变化的对应关系。总的来说就是,看了课本后:正变换,会算了;反变换,会算了;为什么是这两个公式,不知道,但是为了解题强行背过了。对于DTFT及其反变换我们总时无法直观地理解这两种转换公式的特殊意义是什么,这篇文章以我个人理解为主,对DTFT及其反变换进行了直观解释,并且按这个理解思路,公式也不需要再死记硬背。
复数域
复数定义为:
![]()
那么![]()
根据欧拉公式
![]()
得
![]()
![]() 在复平面如下图所示:
在复平面如下图所示:
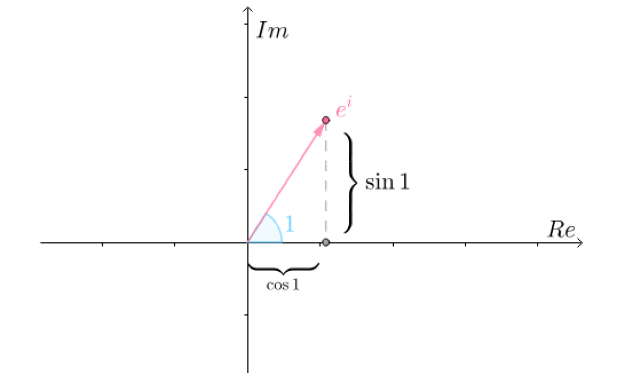
![]() 在复平面如下图所示
在复平面如下图所示
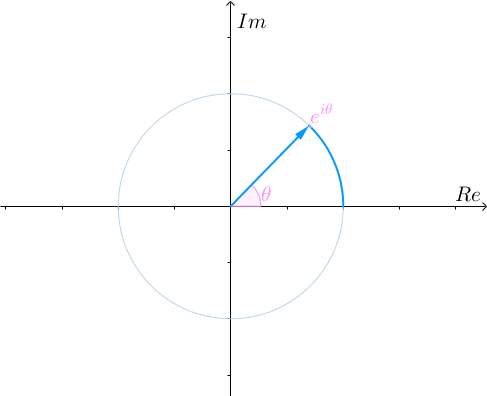
那么![]() 就可以表示为复频域以ω角速度逆时针旋转的信号。
就可以表示为复频域以ω角速度逆时针旋转的信号。
DTFT正变换
离散时间傅里叶变换公式如下

在复平面里,可以用旋转了![]() 角度、模长为
角度、模长为![]() 的图形来表示时间信号
的图形来表示时间信号![]() 。比如,n=2时,对应的复平面信号为
。比如,n=2时,对应的复平面信号为![]() 。
。
那如果已知某时刻复平面的信号,怎么求对应时间的时域信号呢?反向旋转对应的角度,让复数转换为模场不变的实数就好了,即乘以![]() 。
。
那么综上所述,DTFT可以理解为在复平面,顺时针旋转![]() 角度,模长
角度,模长![]() 的所有信号的和。
的所有信号的和。
DTFT反变换
已知![]() 如何将x[n]表示出来呢?
如何将x[n]表示出来呢?
首先,用![]() 乘以
乘以![]() ,这样,就可以将x[n]项筛选出来:此时x[n]项对应的信号为复平面里的实数,其他项均为虚数。
,这样,就可以将x[n]项筛选出来:此时x[n]项对应的信号为复平面里的实数,其他项均为虚数。
然后,所有项一起进行上下限范围差为2π的积分,虚数项通过积分,结果变为了0,实数项通过积分,结果变为原来的2π倍。
最后将以上结果除以2π就可以得到x[n]的值啦。
即:
![]()
相关内容
复指数信号
信号与系统专栏